No CrossRef data available.
Published online by Cambridge University Press: 02 April 2015
We prove that the Schrödinger system
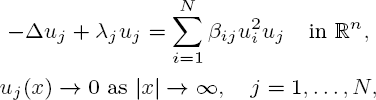
where n = 1, 2, 3, N ≥ 2, λ1 = λ2 = … = λN = 1, βij = βji > 0 for i, j = 1, …, N, has a unique positive solution up to translation if the βij (i ≠ j) are comparatively large with respect to the βjj. The same conclusion holds if n = 1 and if the βij (i ≠ j) are comparatively small with respect to the βjj. Moreover, this solution is a ground state in the sense that it has the least energy among all non-zero solutions provided that the βij (i ≠ j) are comparatively large with respect to the βjj, and it has the least energy among all non-trivial solutions provided that n = 1 and the βij (i ≠ j) are comparatively small with respect to the βjj. In particular, these conclusions hold if βij = (i ≠ j) for some β and either β > max{β11, β22, …, βNN} or n = 1 and 0 < β < min{β11, β22, …, βNN}.