No CrossRef data available.
Article contents
Existence conditions for higher order eigensets of multiparameter operators
Published online by Cambridge University Press: 14 November 2011
Synopsis
We consider classes of self-adjoint operators 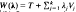 for which the nonpositive part of the spectrum consists of eigenvalues ρ0(λ)≦ ρ1(») ≦ … repeated according to multiplicity. The sets of λ where ρi(λ) is negative and zero are labelled Ni and Zi respectively, and Pi = ℝk\(Ni ∪ Zi). We study conditions on the Vj sufficient to ensure nonemptiness of at least one of Ni, Zi and Pi for all T or for all positive definite T, as well as conditions which are necessary in the sense that failure permits emptiness for at least one T.
for which the nonpositive part of the spectrum consists of eigenvalues ρ0(λ)≦ ρ1(») ≦ … repeated according to multiplicity. The sets of λ where ρi(λ) is negative and zero are labelled Ni and Zi respectively, and Pi = ℝk\(Ni ∪ Zi). We study conditions on the Vj sufficient to ensure nonemptiness of at least one of Ni, Zi and Pi for all T or for all positive definite T, as well as conditions which are necessary in the sense that failure permits emptiness for at least one T.
As an example of our results, we show in the Sturm–Liouville case
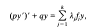
with L∞ coefficients and separated end conditions, that nonemptiness of Zi for all T (i.e. for all p > 0, all q and all boundary data) is equivalent to the i-independent condition that the ftj do not vanish simultaneously on a set of positive measure.
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 103 , Issue 1-2 , 1986 , pp. 137 - 146
- Copyright
- Copyright © Royal Society of Edinburgh 1986

