Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yin-Bing, Deng
1991.
On the superlinear ambrosetti-prodi problem involving critical Sobolev exponents.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 17,
Issue. 12,
p.
1111.
Yinbing, Deng
1992.
Existence of multiple positive solutions for a semilinear equation with critical exponent.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 122,
Issue. 1-2,
p.
161.
Yinbing, Deng
1993.
Existence of multiple positive solutions for $$ - \Delta u = \lambda u + u^{\frac{{N + 2}}{{N - 2}}} + \mu f\left( x \right)*$$.
Acta Mathematica Sinica,
Vol. 9,
Issue. 3,
p.
311.
Cao, Dao-Min
1994.
MULTIPLE POSITIVE SOLUTIONS OF INHOMOGENEOUS SEMILINEAR ELLIPTIC EQUATIONS IN UNBOUNDED DOMAINS IN R 2.
Acta Mathematica Scientia,
Vol. 14,
Issue. 3,
p.
297.
Jianfu, Yang
1995.
Positive solutions of an obstacle problem.
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 4,
Issue. 2,
p.
339.
Li, Gongbao
and
Zhou, Huansong
1995.
The existence of a weak solution of inhomogeneous quasilinear elliptic equation with critical growth conditions.
Acta Mathematica Sinica,
Vol. 11,
Issue. 2,
p.
146.
Dao-Min, Cao
and
Huan-Song, Zhou
1996.
Multiple positive solutions of nonhomogeneous semilinear elliptic equations in ℝN.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 126,
Issue. 2,
p.
443.
Cao, Dao-Min
and
Zhou, Huan-Song
1996.
On the existence of multiple solutions of nonhomogeneous elliptic equations involving critical Sobolev exponents.
ZAMP Zeitschrift f�r angewandte Mathematik und Physik,
Vol. 47,
Issue. 1,
p.
89.
1997.
Variational Methods for Potential Operator Equations.
p.
270.
Zhou, Huansong
1998.
POSITIVE SOLUTIONS FOR NONHOMOGENEOUS ELLIPTIC EQUATIONS WITH CRITICAL GROWTH ON R 2.
Acta Mathematica Scientia,
Vol. 18,
Issue. 2,
p.
124.
Xie, Ziqing
1999.
MULTIPLICITY RESULTS FOR AN INHOMOGENEOUS NONLINEAR ELLIPTIC PROBLEM.
Acta Mathematica Scientia,
Vol. 19,
Issue. 2,
p.
158.
Zhang, Zhengjie
2000.
MULTIPLE SOLUTIONS OF NONHOMOGENEOUS FOR RELATED CHOQUARD’S EQUATION.
Acta Mathematica Scientia,
Vol. 20,
Issue. 3,
p.
374.
Zhengjie, Zhang
2001.
Multiple solutions of nonhomogeneous Chouquard’s equations.
Acta Mathematicae Applicatae Sinica,
Vol. 17,
Issue. 1,
p.
47.
Wang, Gengsheng
2002.
Optimal control problems governed by non-well-posed semilinear elliptic equation.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 49,
Issue. 3,
p.
315.
Deng, Yinbin
Li, Yi
and
Zhao, Xuejin
2003.
MULTIPLE SOLUTIONS FOR AN INHOMOGENEOUS SEMILINEAR ELLIPTIC EQUATION IN R N.
Acta Mathematica Scientia,
Vol. 23,
Issue. 1,
p.
1.
Deng, Yinbin
Ma, Yaming
and
Zhao, Charles Xuejin
2005.
Existence and Properties of Multiple Positive Solutions for Semi-Linear Equations with Critical Exponents.
Rocky Mountain Journal of Mathematics,
Vol. 35,
Issue. 5,
Hsu, Tsing-San
and
Lin, Huei-Li
2005.
Bifurcation of positive entire solutions for a semilinear elliptic equation.
Bulletin of the Australian Mathematical Society,
Vol. 72,
Issue. 3,
p.
349.
Lin, Huei-Li
2006.
Three positive solutions of semilinear elliptic equations in the half space with a hole.
Journal of Differential Equations,
Vol. 230,
Issue. 2,
p.
614.
Hsu, Tsing-San
2006.
Existence of multiple positive solutions of subcritical semilinear elliptic problems in exterior strip domains.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 64,
Issue. 6,
p.
1203.
Hsu, Tsing-San
2006.
Existence and bifurcation for some elliptic problems on exteriorstrip domains.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2006,
Issue. 1,

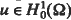 has at least two positive solutions.
has at least two positive solutions.