Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-10T13:11:16.712Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence of solutions for critical Choquard equations via the concentration-compactness method

Part of: Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  26 January 2019

Fashun Gao ,
Edcarlos D. da Silva ,
Minbo Yang  and
Jiazheng Zhou
Fashun Gao
Affiliation:
Department of Mathematics and Physics, Henan University of Urban Construction, Pingdingshan467044, People's Republic of China (fsgao@zjnu.edu.cn)
Edcarlos D. da Silva
Affiliation:
IME C Universidade Federal de Goiás, 74001-970 Goiania, GO, Brazil (eddomingos@hotmail.com)
Minbo Yang
Affiliation:
Department of Mathematics, Zhejiang Normal University, Jinhua321004, People's Republic of China (mbyang@zjnu.edu.cn)
Jiazheng Zhou
Affiliation:
Departamento de Matemática, Universidade de Bras´ilia, 70910-900 Bras´ilia DF, Brazil (jiazzheng@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we consider the nonlinear Choquard equation

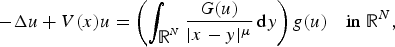$$-\Delta u + V(x)u = \left( {\int_{{\open R}^N} {\displaystyle{{G(u)} \over { \vert x-y \vert ^\mu }}} \,{\rm d}y} \right)g(u)\quad {\rm in}\;{\open R}^N, $$
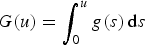where 0 < μ < N, N ⩾ 3, g(u) is of critical growth due to the Hardy–Littlewood–Sobolev inequality and $G(u)=\int ^u_0g(s)\,{\rm d}s$. Firstly, by assuming that the potential V(x) might be sign-changing, we study the existence of Mountain-Pass solution via a nonlocal version of the second concentration- compactness principle. Secondly, under the conditions introduced by Benci and Cerami , we also study the existence of high energy solution by using a nonlocal version of global compactness lemma.

Keywords

Critical Choquard equationHardy–Littlewood–Sobolev inequalityConcentration-Compactness principle

MSC classification

Primary: 35J20: Variational methods for second-order elliptic equations
Secondary: 35J60: Nonlinear elliptic equations 35A15: Variational methods
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 2 , April 2020 , pp. 921 - 954
Copyright
Copyright © Royal Society of Edinburgh 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Ackermann, N.. On a periodic Schrödinger equation with nonlocal superlinear part. Math. Z. 248 (2004), 423–443.CrossRefGoogle Scholar
2Alves, C. O. and Yang, M.. Existence of semiclassical ground state solutions for a generalized Choquard equation. J. Diff. Equ. 257 (2014), 4133–4164.CrossRefGoogle Scholar
3Alves, C. O. and Yang, M.. Multiplicity and concentration behavior of solutions for a quasilinear Choquard equation via penalization method. Proc. Roy. Soc. Edinburgh Sect. A 146 (2016), 23–58.CrossRefGoogle Scholar
4Alves, C. O., Cassani, D., Tarsi, C. and Yang, M.. Existence and concentration of ground state solutions for a critical nonlocal Schrödinger equation in ℝ 2. J. Diff. Equ. 261 (2014), 1933–1972.CrossRefGoogle Scholar
5Alves, C. O., Nóbrega, A. B. and Yang, M.. Multi-bump solutions for Choquard equation with deepening potential well. Calc. Var. Partial Diff. Equ. 55 (2016), 28 pp.CrossRefGoogle Scholar
6Alves, C. O., Gao, F., Squassina, M. and Yang, M.. Singularly perturbed critical Choquard equations. J. Diff. Equ. 263 (2017), 3943–3988.CrossRefGoogle Scholar
7Benci, V. and Cerami, G.. Existence of positive solutions of the equation $-\Delta u+a(x)u=u^(N+2)/(N-2)$ in ℝN. J. Funct. Anal. 88 (1990), 90–117.CrossRefGoogle Scholar
8Ben-Naoum, A. K., Troestler, C. and Willem, M.. Extrema problems with critical Sobolev exponents on unbounded domains. Nonlinear Anal. 26 (1996), 823–833.CrossRefGoogle Scholar
9Bianchi, G., Chabrowski, J. and Szulkin, A.. On symmetric solutions of an elliptic equation with a nonlinearity involving critical Sobolev exponent. Nonlinear Anal. 25 (1995), 41–59.CrossRefGoogle Scholar
10Brézis, H. and Lieb, E.. A relation between pointwise convergence of functions and convergence of functionals. Proc. Amer. Math. Soc. 88 (1983), 486–490.CrossRefGoogle Scholar
11Buffoni, B., Jeanjean, L. and Stuart, C. A.. Existence of a nontrivial solution to a strongly indefinite semilinear equation. Proc. Amer. Math. Soc. 119 (1993), 179–186.10.1090/S0002-9939-1993-1145940-XCrossRefGoogle Scholar
12Cassani, D., Van Schaftingen, J. and Zhang, J.. Groundstates for Choquard type equations with Hardy-Littlewood-Sobolev lower critical exponent, 2017, arXiv: 1709.09448.Google Scholar
13Chabrowski, J.. Concentration-compactness principle at infinity and semilinear elliptic equations involving critical and subcritical Sobolev exponents. Calc. Var. Partial Diff. Equ. 3 (1995), 493–512.CrossRefGoogle Scholar
14Cingolani, S., Secchi, S. and Squassina, M.. Semi-classical limit for Schrödinger equations with magnetic field and Hartree-type nonlinearities. Proc. Roy. Soc. Edinburgh Sect. A 140 (2010), 973–1009.CrossRefGoogle Scholar
15Cingolani, S., Clapp, M. and Secchi, S.. Multiple solutions to a magnetic nonlinear Choquard equation. Z. Angew. Math. Phys. 63 (2012), 233–248.CrossRefGoogle Scholar
16Ding, Y., Gao, F. and Yang, M.. Semiclassical states for a class of Choquard type equations with critical growth: critical frequency case, 2017, arXiv: 1710.05255.Google Scholar
17Ding, Y. H. and Lin, F. H.. Solutions of perturbed Schrödinger equations with critical nonlinearity. Calc. Var. Partial Diff. Equ. 30 (2007), 231–249.CrossRefGoogle Scholar
18Gao, F. and Yang, M.. Brezis-Nirenberg type critical problem for nonlinear Choquard equation. Sci. China Math. 61 (2018), 1219–1242.CrossRefGoogle Scholar
19Gao, F. and Yang, M.. On nonlocal Choquard equations with Hardy–Littlewood–Sobolev critical exponents. J. Math. Anal. Appl. 448 (2017), 1006–1041.CrossRefGoogle Scholar
20Gao, F. and Yang, M.. A strongly indefinite Choquard equation with critical exponent due to Hardy–Littlewood–Sobolev inequality. Commun. Contemp. Math. 20 (2018), 1750037, 22 pp.CrossRefGoogle Scholar
21Lieb, E. H.. Existence and uniqueness of the minimizing solution of Choquard's nonlinear equation. Studies Appl. Math. 57 (1976/77), 93–105.CrossRefGoogle Scholar
22Lieb, E. H. and Loss, M.. Analysis (AMS, Providence, Rhode Island: Gradute Studies in Mathematics, 2001).Google Scholar
23Lions, P. L.. The Choquard equation and related questions. Nonlinear Anal. 4 (1980), 1063–1072.CrossRefGoogle Scholar
24Lions, P. L.. The concentration-compactness principle in the calculus of variations, The locally compact case, Part 1. Ann. Inst. H. Poincaré Anal. Non Linéaire 1 (1984a), 109–145.10.1016/S0294-1449(16)30428-0CrossRefGoogle Scholar
25Lions, P. L.. The concentration-compactness principle in the calculus of variations, The locally compact case, Part 2. Ann. Inst. H. Poincaré Anal. Non Linéaire 1 (1984b), 223–283.CrossRefGoogle Scholar
26Lions, P. L.. The concentration-compactness principle in the calculus of variations, The limit case, Part 1. Rev. Mat. Iberoamericana 1 (1985a), 145–201.CrossRefGoogle Scholar
27Lions, P. L.. The concentration-compactness principle in the calculus of variations, The limit case, Part 2. Rev. Mat. Iberoamericana 1 (1985b), 45–121.CrossRefGoogle Scholar
28Ma, L. and Zhao, L.. Classification of positive solitary solutions of the nonlinear Choquard equation. Arch. Ration. Mech. Anal. 195 (2010), 455–467.CrossRefGoogle Scholar
29Moroz, V., Van Schaftingen, J.. Groundstates of nonlinear Choquard equations: Existence, qualitative properties and decay asymptotics. J. Funct. Anal. 265 (2013), 153–184.CrossRefGoogle Scholar
30Moroz, V. and Van Schaftingen, J.. Existence of groundstates for a class of nonlinear Choquard equations. Trans. Amer. Math. Soc. 367 (2015a), 6557–6579.CrossRefGoogle Scholar
31Moroz, V., Van Schaftingen, J.. Groundstates of nonlinear Choquard equation: Hardy–Littlewood–Sobolev critical exponent. Commun. Contemp. Math 17 (2015b), Article ID 1550005, 12 pp.CrossRefGoogle Scholar
32Moroz, V. and Van Schaftingen, J.. Semi-classical states for the Choquard equation. Calc. Var. Partial Diff. Equ. 52 (2015c), 199–235.CrossRefGoogle Scholar
33Pekar, S.. Untersuchungüber die Elektronentheorie der Kristalle (Berlin: Akademie Verlag, 1954).Google Scholar
34Penrose, R.. On gravity's role in quantum state reduction. Gen. Relativ. Gravitat. 28 (1996), 581–600.CrossRefGoogle Scholar
35Shen, Z., Gao, F. and Yang, M.. On the critical Choquard equation with potential well. Discrete Contin. Dyn. Syst. A 7 (2018), 3567–3593.CrossRefGoogle Scholar
36Struwe, M.. A global compactness result for elliptic boundary value problems involving limiting nonlinearities. Math. Z. 187 (1984), 511–517.CrossRefGoogle Scholar
37Wei, J.C. and Winter, M.. Strongly interacting bumps for the Schrödinger–Newton equations. J. Math. Phys. 50 (2009), 012905, 22 pp.CrossRefGoogle Scholar
38Willem, M.. Minimax Theorems, Progress in Nonlinear Differential Equations and their Applications, 24 (Boston, MA: Birkhäuser Boston, Inc., 1996).Google Scholar
39Zou, H.. Existence and non-existence for Schrödinger equations involving critical Sobolev exponents. J. Korean Math. Soc. 47 (2010), 547–572.CrossRefGoogle Scholar