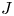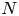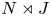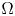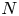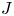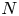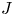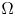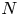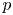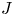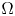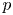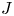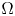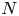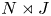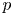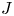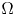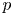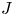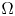1. Introduction
Suppose a finite group $J$![]() acts via automorphisms on a finite group $N$
acts via automorphisms on a finite group $N$![]() and the induced semi-direct product $G= N \rtimes J$
and the induced semi-direct product $G= N \rtimes J$![]() acts on some non-empty set $\Omega$
acts on some non-empty set $\Omega$![]() where the action of $N$
where the action of $N$![]() is transitive. Glauberman showed that if each supplement $H$
is transitive. Glauberman showed that if each supplement $H$![]() of $N$
of $N$![]() in $G$
in $G$![]() splits over $N \cap H$
splits over $N \cap H$![]() and each complement of $N$
and each complement of $N$![]() in $G$
in $G$![]() is conjugate to $J$
is conjugate to $J$![]() , then there exists a $J$
, then there exists a $J$![]() -invariant element $\omega \in \Omega$
-invariant element $\omega \in \Omega$![]() . Consequently, if the orders of $J$
. Consequently, if the orders of $J$![]() and $N$
and $N$![]() are coprime so that the Schur–Zassenhaus theorem applies, a fixed point always exists [Reference Glauberman4, Thm. 4]. In this note, we consider the non-coprime case and establish some conditions for the existence of a fixed point.
are coprime so that the Schur–Zassenhaus theorem applies, a fixed point always exists [Reference Glauberman4, Thm. 4]. In this note, we consider the non-coprime case and establish some conditions for the existence of a fixed point.
Given an action as described above, consider the stabiliser $G_\alpha \leq G$![]() fixing an arbitrary point $\alpha \in \Omega$
fixing an arbitrary point $\alpha \in \Omega$![]() . As $N$
. As $N$![]() is transitive, $G_\alpha$
is transitive, $G_\alpha$![]() supplements $N$
supplements $N$![]() in $G$
in $G$![]() . In this context, $J$
. In this context, $J$![]() fixes an element of $\Omega$
fixes an element of $\Omega$![]() if and only if the following two conditions are met. Firstly, we must ensure $G_\alpha$
if and only if the following two conditions are met. Firstly, we must ensure $G_\alpha$![]() splits over $N\cap G_\alpha$
splits over $N\cap G_\alpha$![]() so that there exists some complement $J'$
so that there exists some complement $J'$![]() . As $G/N \cong G_\alpha /(N\cap G_\alpha )$
. As $G/N \cong G_\alpha /(N\cap G_\alpha )$![]() , it will follow that $J'$
, it will follow that $J'$![]() also complements $N$
also complements $N$![]() in $G$
in $G$![]() . Secondly, we require that $J' = g^{-1}Jg$
. Secondly, we require that $J' = g^{-1}Jg$![]() for some $g\in G$
for some $g\in G$![]() so that $J$
so that $J$![]() fixes $g\cdot \alpha$
fixes $g\cdot \alpha$![]() . For the latter requirement, we concern ourselves with conditions for two specific complements in a semidirect product to be conjugate.
. For the latter requirement, we concern ourselves with conditions for two specific complements in a semidirect product to be conjugate.
To this end, we say two subgroups $H$![]() and $H'$
and $H'$![]() are locally conjugate in a group $G$
are locally conjugate in a group $G$![]() if for each prime $p$
if for each prime $p$![]() , a Sylow $p$
, a Sylow $p$![]() -subgroup of $H$
-subgroup of $H$![]() is conjugate to a Sylow $p$
is conjugate to a Sylow $p$![]() -subgroup of $H'$
-subgroup of $H'$![]() . Losey and Stonehewer showed that if $H$
. Losey and Stonehewer showed that if $H$![]() and $H'$
and $H'$![]() are locally conjugate supplements of some normal nilpotent subgroup $N$
are locally conjugate supplements of some normal nilpotent subgroup $N$![]() in a soluble group $G$
in a soluble group $G$![]() , then $H$
, then $H$![]() and $H'$
and $H'$![]() are conjugate if either $G/N$
are conjugate if either $G/N$![]() is nilpotent or $N$
is nilpotent or $N$![]() is abelian [Reference Losey and Stonehewer7]. Evans and Shin further showed that if $N$
is abelian [Reference Losey and Stonehewer7]. Evans and Shin further showed that if $N$![]() is abelian, then $G$
is abelian, then $G$![]() need not be soluble [Reference Evans and Shin3].
need not be soluble [Reference Evans and Shin3].
We first restrict $N$![]() to be abelian and use a decomposition result from group cohomology to provide an alternate proof of:
to be abelian and use a decomposition result from group cohomology to provide an alternate proof of:
Lemma 1.1 (Evans and Shin)
In a finite group, two complements of a normal abelian subgroup are conjugate if and only if they are locally conjugate.
We use this, along with Gaschütz's result that a finite group $G$![]() splits over an abelian subgroup $N$
splits over an abelian subgroup $N$![]() if and only if for each prime $p$
if and only if for each prime $p$![]() , a Sylow $p$
, a Sylow $p$![]() -subgroup $S$
-subgroup $S$![]() of $G$
of $G$![]() splits over $N\cap S$
splits over $N\cap S$![]() , to show:
, to show:
Theorem 1.2 Given a finite group $J$![]() acting via automorphisms on a finite abelian group $N$
acting via automorphisms on a finite abelian group $N$![]() , suppose the induced semidirect product $N\rtimes J$
, suppose the induced semidirect product $N\rtimes J$![]() acts on some non-empty set $\Omega$
acts on some non-empty set $\Omega$![]() where the action of $N$
where the action of $N$![]() is transitive. If for each prime $p$
is transitive. If for each prime $p$![]() , a Sylow $p$
, a Sylow $p$![]() -subgroup of $J$
-subgroup of $J$![]() fixes an element of $\Omega$
fixes an element of $\Omega$![]() , then there exists some $J$
, then there exists some $J$![]() -invariant element $\omega \in \Omega$
-invariant element $\omega \in \Omega$![]() .
.
This had previously been shown using elementary arguments for the special case that $J$![]() is supersoluble [Reference Burkhart2, Cor. 2]. The theorem implies:
is supersoluble [Reference Burkhart2, Cor. 2]. The theorem implies:
Corollary 1.3 Let $G$![]() be a finite split extension over an abelian subgroup $N$
be a finite split extension over an abelian subgroup $N$![]() . If for each prime $p$
. If for each prime $p$![]() there is a Sylow $p$
there is a Sylow $p$![]() -subgroup $S$
-subgroup $S$![]() of $G$
of $G$![]() such that any two complements of $N\cap S$
such that any two complements of $N\cap S$![]() in $S$
in $S$![]() are conjugate, then any two complements of $N$
are conjugate, then any two complements of $N$![]() in $G$
in $G$![]() are $G$
are $G$![]() -conjugate.
-conjugate.
This extends a result of D. G. Higman [Reference Higman5, Cor. 2] that requires the complements of $N\cap S$![]() in $S$
in $S$![]() to be conjugate within $S$
to be conjugate within $S$![]() .
.
We then consider nilpotent $N$![]() and supersoluble $N\rtimes J$
and supersoluble $N\rtimes J$![]() . We adapt our approach for lemma 1.1 to nonabelian cohomology and demonstrate:
. We adapt our approach for lemma 1.1 to nonabelian cohomology and demonstrate:
Lemma 1.4 In a finite supersoluble group, two complements of a normal nilpotent subgroup are conjugate if and only if they are locally conjugate.
With this, we then show:
Theorem 1.5 Given a finite group $J$![]() acting via automorphisms on a finite nilpotent group $N$
acting via automorphisms on a finite nilpotent group $N$![]() , suppose the induced semidirect product $N\rtimes J$
, suppose the induced semidirect product $N\rtimes J$![]() is supersoluble and acts on some non-empty set $\Omega$
is supersoluble and acts on some non-empty set $\Omega$![]() where the action of $N$
where the action of $N$![]() is transitive. If for each prime $p$
is transitive. If for each prime $p$![]() , a Sylow $p$
, a Sylow $p$![]() -subgroup of $J$
-subgroup of $J$![]() fixes an element of $\Omega$
fixes an element of $\Omega$![]() , then there exists some $J$
, then there exists some $J$![]() -invariant element $\omega \in \Omega$
-invariant element $\omega \in \Omega$![]() .
.
The theorem also implies an analogue of corollary 1.3 that we state and prove in § 3.
1.1 Outline
We proceed as follows. In the remainder of this section, we introduce notation and some conventions from group cohomology. In the next section, we restrict $N$![]() to be abelian and prove theorem 1.2. We then restrict $N$
to be abelian and prove theorem 1.2. We then restrict $N$![]() to be nilpotent and $N\rtimes J$
to be nilpotent and $N\rtimes J$![]() to be supersoluble in § 3 and prove theorem 1.5, before concluding in § 4.
to be supersoluble in § 3 and prove theorem 1.5, before concluding in § 4.
1.2 Notation and conventions
All groups in this note are assumed finite. A subgroup $K\leq G$![]() supplements $N\vartriangleleft G$
supplements $N\vartriangleleft G$![]() if $G=NK$
if $G=NK$![]() and complements $N$
and complements $N$![]() if it both supplements $N$
if it both supplements $N$![]() and the intersection $N\cap K$
and the intersection $N\cap K$![]() is trivial. We denote conjugation by $g^\gamma = \gamma ^{-1}g\gamma$
is trivial. We denote conjugation by $g^\gamma = \gamma ^{-1}g\gamma$![]() for $g,\,\gamma \in G$
for $g,\,\gamma \in G$![]() and otherwise let groups act from the left. For a prime $p$
and otherwise let groups act from the left. For a prime $p$![]() , we let $\operatorname {Syl}_p(G)$
, we let $\operatorname {Syl}_p(G)$![]() denote the set of Sylow $p$
denote the set of Sylow $p$![]() -subgroups of a group $G$
-subgroups of a group $G$![]() .
.
We rely on rudimentary notions from group cohomology that can be found in the texts of Brown [Reference Brown1] and Serre [Reference Serre8]. Given a group $J$![]() acting on a group $N$
acting on a group $N$![]() via automorphisms, crossed homomorphisms or 1-cocycles are maps $\varphi : J \to N$
via automorphisms, crossed homomorphisms or 1-cocycles are maps $\varphi : J \to N$![]() satisfying $\varphi (jj') = \varphi (j) \varphi (j')^{j^{-1}}$
satisfying $\varphi (jj') = \varphi (j) \varphi (j')^{j^{-1}}$![]() for all $j,\,j' \in J$
for all $j,\,j' \in J$![]() . Two such maps $\varphi$
. Two such maps $\varphi$![]() and $\varphi '$
and $\varphi '$![]() are cohomologous if there exists $n\in N$
are cohomologous if there exists $n\in N$![]() such that $\varphi '(j) = n^{-1} \varphi (j) n^{j^{-1}}$
such that $\varphi '(j) = n^{-1} \varphi (j) n^{j^{-1}}$![]() for all $j\in J$
for all $j\in J$![]() ; in this case, we write $\varphi \sim \varphi '$
; in this case, we write $\varphi \sim \varphi '$![]() . We take the first cohomology $H^1(J,\,N)$
. We take the first cohomology $H^1(J,\,N)$![]() to be the pointed set $Z^1(J,\,N)$
to be the pointed set $Z^1(J,\,N)$![]() of crossed homomorphisms modulo this equivalence. The distinguished point corresponds to the equivalence class containing the map taking each element of $J$
of crossed homomorphisms modulo this equivalence. The distinguished point corresponds to the equivalence class containing the map taking each element of $J$![]() to the identity of $N$
to the identity of $N$![]() . Our interest in this set stems primarily from the well-known bijective correspondence [Reference Serre8, Exer. 1 in §I.5.1] between it and the $N$
. Our interest in this set stems primarily from the well-known bijective correspondence [Reference Serre8, Exer. 1 in §I.5.1] between it and the $N$![]() -conjugacy classes of complements to $N$
-conjugacy classes of complements to $N$![]() in $N\rtimes J$
in $N\rtimes J$![]() . Specifically, for each $\varphi \in Z^1(J,\,N)$
. Specifically, for each $\varphi \in Z^1(J,\,N)$![]() , the subgroup $F(\varphi ) = \{ \varphi (j)j \}_{j\in J}$
, the subgroup $F(\varphi ) = \{ \varphi (j)j \}_{j\in J}$![]() complements $N$
complements $N$![]() in $NJ$
in $NJ$![]() and all such complements may be written in this way. Two crossed homomorphisms yield conjugate complements under $F$
and all such complements may be written in this way. Two crossed homomorphisms yield conjugate complements under $F$![]() if and only if they are cohomologous, so $F$
if and only if they are cohomologous, so $F$![]() induces the desired correspondence.
induces the desired correspondence.
For a subgroup $K\leq J$![]() , we let $\varphi |_{K}$
, we let $\varphi |_{K}$![]() denote the restriction of $\varphi \in Z^1(J,\,N)$
denote the restriction of $\varphi \in Z^1(J,\,N)$![]() to $K$
to $K$![]() and $\operatorname {res}^J_K: H^1(J,\,N) \to H^1(K,\,N)$
and $\operatorname {res}^J_K: H^1(J,\,N) \to H^1(K,\,N)$![]() be the map induced in cohomology. For $\varphi \in Z^1(K,\,N)$
be the map induced in cohomology. For $\varphi \in Z^1(K,\,N)$![]() and $j\in J$
and $j\in J$![]() , define $\varphi ^j(x) = \varphi (x^{j^{-1}})^{j}$
, define $\varphi ^j(x) = \varphi (x^{j^{-1}})^{j}$![]() . We call $\varphi$
. We call $\varphi$![]() $J$
$J$![]() -invariant if $\operatorname {res}^K_{K\cap K^j} \varphi \sim \operatorname {res}^{K^j}_{K\cap K^j} \varphi ^j$
-invariant if $\operatorname {res}^K_{K\cap K^j} \varphi \sim \operatorname {res}^{K^j}_{K\cap K^j} \varphi ^j$![]() for all $j\in J$
for all $j\in J$![]() and let $\operatorname {inv}_J H^1(K,\,N)$
and let $\operatorname {inv}_J H^1(K,\,N)$![]() denote the set of $J$
denote the set of $J$![]() -invariant elements in $H^1(K,\,N)$
-invariant elements in $H^1(K,\,N)$![]() . For any $\varphi \in Z^1(J,\,N)$
. For any $\varphi \in Z^1(J,\,N)$![]() , we have $\varphi ^j(x) = n^{-1} \varphi (x) n^{x^{-1}}$
, we have $\varphi ^j(x) = n^{-1} \varphi (x) n^{x^{-1}}$![]() where $n= \varphi (j^{-1})$
where $n= \varphi (j^{-1})$![]() so that $\varphi ^j \sim \varphi$
so that $\varphi ^j \sim \varphi$![]() . In particular, $\operatorname {res}^J_K H^1(J,\,N) \subseteq \operatorname {inv}_J H^1(K,\, N)$
. In particular, $\operatorname {res}^J_K H^1(J,\,N) \subseteq \operatorname {inv}_J H^1(K,\, N)$![]() .
.
2. $N$ is abelian
is abelian
In this section, we restrict $N$![]() to be abelian so that $H^1(J,\,N)$
to be abelian so that $H^1(J,\,N)$![]() takes the form of an abelian group. We first prove lemma 1.1 as stated in § 1.
takes the form of an abelian group. We first prove lemma 1.1 as stated in § 1.
Proof of lemma 1.1 Suppose we are given locally conjugate complements $J$![]() and $J'$
and $J'$![]() of a normal abelian subgroup $N$
of a normal abelian subgroup $N$![]() in some group $G$
in some group $G$![]() . As any element $g\in G$
. As any element $g\in G$![]() may be uniquely written $g=jn$
may be uniquely written $g=jn$![]() for $j\in J$
for $j\in J$![]() and $n\in N$
and $n\in N$![]() , for each prime $p$
, for each prime $p$![]() we have $J_p' = (J_p)^n$
we have $J_p' = (J_p)^n$![]() for some $J_p\in \operatorname {Syl}_p(J)$
for some $J_p\in \operatorname {Syl}_p(J)$![]() , $J_p' \in \operatorname {Syl}_p(J')$
, $J_p' \in \operatorname {Syl}_p(J')$![]() , and $n\in N$
, and $n\in N$![]() . Let $\varphi '\in Z^1(J,\,N)$
. Let $\varphi '\in Z^1(J,\,N)$![]() denote the crossed homomorphism corresponding to $J'$
denote the crossed homomorphism corresponding to $J'$![]() . It suffices to show that $\varphi '\sim 1$
. It suffices to show that $\varphi '\sim 1$![]() , where $1\in Z^1(J,\,N)$
, where $1\in Z^1(J,\,N)$![]() denotes the map taking each element of $J$
denotes the map taking each element of $J$![]() to the identity of $N$
to the identity of $N$![]() . Through the $p$
. Through the $p$![]() -primary decomposition of $H^1(J,\,N)$
-primary decomposition of $H^1(J,\,N)$![]() , we have the isomorphism [Reference Brown1, §III.10]:
, we have the isomorphism [Reference Brown1, §III.10]:
where $\mathcal {D}$![]() is the set of prime divisors of $\left\lvert{J}\right\rvert$
is the set of prime divisors of $\left\lvert{J}\right\rvert$![]() and the $J_p$
and the $J_p$![]() are those given above. For every $p\in \mathcal {D}$
are those given above. For every $p\in \mathcal {D}$![]() , we see that $\varphi '|_{J_p}\sim 1|_{J_p}$
, we see that $\varphi '|_{J_p}\sim 1|_{J_p}$![]() as $J_p$
as $J_p$![]() and $J_p'$
and $J_p'$![]() are $N$
are $N$![]() -conjugate complements of $N$
-conjugate complements of $N$![]() in $NJ_p$
in $NJ_p$![]() . Thus, $\varphi '$
. Thus, $\varphi '$![]() maps to the identity in each direct summand on the right-hand side of (2.1) and we may conclude $\varphi '\sim 1$
maps to the identity in each direct summand on the right-hand side of (2.1) and we may conclude $\varphi '\sim 1$![]() so that $J$
so that $J$![]() and $J'$
and $J'$![]() are conjugate.
are conjugate.
We can now use the lemma and Gaschütz's theorem to prove theorem 1.2.
Proof of theorem 1.2 Given $J$![]() , $N$
, $N$![]() , and $\Omega$
, and $\Omega$![]() as described in the hypotheses of the theorem, let $G= N \rtimes J$
as described in the hypotheses of the theorem, let $G= N \rtimes J$![]() denote the induced semidirect product and consider the stabiliser subgroup $G_\alpha$
denote the induced semidirect product and consider the stabiliser subgroup $G_\alpha$![]() for some fixed $\alpha \in \Omega$
for some fixed $\alpha \in \Omega$![]() . As $N$
. As $N$![]() acts transitively, any $g\in G$
acts transitively, any $g\in G$![]() may be written $g\cdot \alpha = n\cdot \alpha$
may be written $g\cdot \alpha = n\cdot \alpha$![]() for some $n\in N$
for some $n\in N$![]() , so that $n^{-1}g \in G_\alpha$
, so that $n^{-1}g \in G_\alpha$![]() . Thus, $G=NG_\alpha$
. Thus, $G=NG_\alpha$![]() .
.
We claim $G_\alpha$![]() splits over $N\cap G_\alpha$
splits over $N\cap G_\alpha$![]() . For any prime $p$
. For any prime $p$![]() , there exists by hypothesis some $n\in N$
, there exists by hypothesis some $n\in N$![]() and $P \in \operatorname {Syl}_p(J)$
and $P \in \operatorname {Syl}_p(J)$![]() such that $P^n \leq G_\alpha$
such that $P^n \leq G_\alpha$![]() . Let $L\in \operatorname {Syl}_p(N\cap G_\alpha )$
. Let $L\in \operatorname {Syl}_p(N\cap G_\alpha )$![]() . As $\left\lvert{G_\alpha }\right\rvert = \left\lvert{N\cap G_\alpha }\right\rvert[G:N]$
. As $\left\lvert{G_\alpha }\right\rvert = \left\lvert{N\cap G_\alpha }\right\rvert[G:N]$![]() , it follows that $S=LP^n \in \operatorname {Syl}_p(G_\alpha )$
, it follows that $S=LP^n \in \operatorname {Syl}_p(G_\alpha )$![]() so $P^n$
so $P^n$![]() complements $S \cap N = L$
complements $S \cap N = L$![]() in $S$
in $S$![]() . As the choice of prime $p$
. As the choice of prime $p$![]() was arbitrary, we may apply Gaschütz's theorem to conclude that $G_\alpha$
was arbitrary, we may apply Gaschütz's theorem to conclude that $G_\alpha$![]() splits over $N\cap G_\alpha$
splits over $N\cap G_\alpha$![]() .
.
Let $J'$![]() complement $N\cap G_\alpha$
complement $N\cap G_\alpha$![]() in $G_\alpha$
in $G_\alpha$![]() . As $G/N \cong G_\alpha / (N \cap G_\alpha )$
. As $G/N \cong G_\alpha / (N \cap G_\alpha )$![]() , it follows that $J'$
, it follows that $J'$![]() also complements $N$
also complements $N$![]() in $G$
in $G$![]() . Lemma 1.1 then implies that $J' = J^g$
. Lemma 1.1 then implies that $J' = J^g$![]() for some $g\in G$
for some $g\in G$![]() so that $J$
so that $J$![]() fixes $\omega = g\cdot \alpha$
fixes $\omega = g\cdot \alpha$![]() .
.
Finally, we outline how corollary 1.3 follows from theorem 1.2.
Proof of corollary 1.2 Given a group $G$![]() satisfying the hypotheses of the corollary, suppose $J$
satisfying the hypotheses of the corollary, suppose $J$![]() and $J'$
and $J'$![]() each complement $N$
each complement $N$![]() in $G$
in $G$![]() . Then $G$
. Then $G$![]() acts on the cosets $\Omega = G/J'$
acts on the cosets $\Omega = G/J'$![]() in such a way that we may apply theorem 1.2 to infer that $J$
in such a way that we may apply theorem 1.2 to infer that $J$![]() fixes $gJ'$
fixes $gJ'$![]() for some $g\in G$
for some $g\in G$![]() . Therefore, $J$
. Therefore, $J$![]() and $J'$
and $J'$![]() are conjugate. As the choice of complements was arbitrary, we may conclude.
are conjugate. As the choice of complements was arbitrary, we may conclude.
3. $N$ is nilpotent and $N\rtimes J$
is nilpotent and $N\rtimes J$ is supersoluble
is supersoluble
In this section, we suppose that $N$![]() is nilpotent and $N \rtimes J$
is nilpotent and $N \rtimes J$![]() is supersoluble. Consequently, $N$
is supersoluble. Consequently, $N$![]() decomposes as the direct sum $N\cong \oplus _{p\in \mathcal {D}} N_p$
decomposes as the direct sum $N\cong \oplus _{p\in \mathcal {D}} N_p$![]() over its characteristic Sylow $p$
over its characteristic Sylow $p$![]() -subgroups $N_p$
-subgroups $N_p$![]() where $\mathcal {D}$
where $\mathcal {D}$![]() denotes the set of prime divisors of $\lvert{N}\rvert$
denotes the set of prime divisors of $\lvert{N}\rvert$![]() . Direct calculations show that the natural projections $N \to N_p$
. Direct calculations show that the natural projections $N \to N_p$![]() induce an isomorphism of pointed sets
induce an isomorphism of pointed sets
To parse the components on the right-hand side of (3.1), we introduce the following:
Proposition 3.1 Suppose a group $J$![]() acts on a $p$
acts on a $p$![]() -group $N$
-group $N$![]() via automorphisms, so that the induced semidirect product $N\rtimes J$
via automorphisms, so that the induced semidirect product $N\rtimes J$![]() is supersoluble. Then $\operatorname {res}_{J_p}^J: H^1(J,\,N) \to \operatorname {inv}_J H^1(J_p,\,N)$
is supersoluble. Then $\operatorname {res}_{J_p}^J: H^1(J,\,N) \to \operatorname {inv}_J H^1(J_p,\,N)$![]() is an isomorphism for $J_p\in \operatorname {Syl}_p(J)$
is an isomorphism for $J_p\in \operatorname {Syl}_p(J)$![]() .
.
Proof. We induct on the order of $J$![]() . If $J$
. If $J$![]() itself is a $p$
itself is a $p$![]() -group, the conclusion is immediate. If $p$
-group, the conclusion is immediate. If $p$![]() is not a divisor of $\lvert{J}\rvert$
is not a divisor of $\lvert{J}\rvert$![]() , the lemma follows from the Schur–Zassenhaus theorem. Otherwise, let $Q\vartriangleleft J$
, the lemma follows from the Schur–Zassenhaus theorem. Otherwise, let $Q\vartriangleleft J$![]() be a Sylow $q$
be a Sylow $q$![]() -subgroup where $q$
-subgroup where $q$![]() is the largest prime divisor of $\lvert{J}\rvert$
is the largest prime divisor of $\lvert{J}\rvert$![]() [Reference Isaacs6, Exer. 3B.10] so that $J\cong Q \rtimes M$
[Reference Isaacs6, Exer. 3B.10] so that $J\cong Q \rtimes M$![]() for some Hall $q'$
for some Hall $q'$![]() -subgroup $M\leq J$
-subgroup $M\leq J$![]() . Consider the inflation–restriction exact sequence [Reference Serre8, §I.5.8],
. Consider the inflation–restriction exact sequence [Reference Serre8, §I.5.8],
where $N^Q$![]() denotes the elements of $N$
denotes the elements of $N$![]() fixed by $Q$
fixed by $Q$![]() .
.
If $q\ne p$![]() , then $H^1(Q,\,N)$
, then $H^1(Q,\,N)$![]() is trivial so that $H^1(J,\,N) \cong H^1(M,\, N^Q)$
is trivial so that $H^1(J,\,N) \cong H^1(M,\, N^Q)$![]() . In the supersoluble group $NQ$
. In the supersoluble group $NQ$![]() , $Q$
, $Q$![]() is a Sylow $q$
is a Sylow $q$![]() -subgroup for the largest prime divisor of $\lvert{NQ}\rvert$
-subgroup for the largest prime divisor of $\lvert{NQ}\rvert$![]() , so that $Q\vartriangleleft N Q$
, so that $Q\vartriangleleft N Q$![]() and $N^Q = N$
and $N^Q = N$![]() . Consequently, $H^1(J,\,N) \cong H^1(M,\, N)$
. Consequently, $H^1(J,\,N) \cong H^1(M,\, N)$![]() . We claim that $\operatorname {res}^J_M$
. We claim that $\operatorname {res}^J_M$![]() affords this isomorphism. It suffices to show that $\operatorname {res}^J_M$
affords this isomorphism. It suffices to show that $\operatorname {res}^J_M$![]() is surjective. For any $\varphi \in Z^1(M,\, N)$
is surjective. For any $\varphi \in Z^1(M,\, N)$![]() , we may define $\tilde \varphi : J \to N$
, we may define $\tilde \varphi : J \to N$![]() by $\tilde \varphi (qm) = \varphi (m)$
by $\tilde \varphi (qm) = \varphi (m)$![]() for $q\in Q$
for $q\in Q$![]() and $m\in M$
and $m\in M$![]() . This map is well-defined as $J\cong Q \rtimes M$
. This map is well-defined as $J\cong Q \rtimes M$![]() . For $q,\,q'\in Q$
. For $q,\,q'\in Q$![]() and $m,\,m'\in M$
and $m,\,m'\in M$![]() , we have $\tilde \varphi (qmq'm') = \varphi (mm') = \varphi (m)\varphi (m')^{m^{-1}} = \tilde \varphi (qm)\tilde \varphi (q'm')^{(qm)^{-1}}$
, we have $\tilde \varphi (qmq'm') = \varphi (mm') = \varphi (m)\varphi (m')^{m^{-1}} = \tilde \varphi (qm)\tilde \varphi (q'm')^{(qm)^{-1}}$![]() , where the last equality follows from the fact that elements of $N$
, where the last equality follows from the fact that elements of $N$![]() commute with elements of $Q$
commute with elements of $Q$![]() . Thus, $\tilde \varphi \in Z^1(J,\, N)$
. Thus, $\tilde \varphi \in Z^1(J,\, N)$![]() . As $\tilde \varphi |_M = \varphi$
. As $\tilde \varphi |_M = \varphi$![]() , we conclude $\operatorname {res}^J_M$
, we conclude $\operatorname {res}^J_M$![]() is surjective.
is surjective.
Exchanging $M$![]() for a conjugate if necessary, we may assume that $J_p \leq M$
for a conjugate if necessary, we may assume that $J_p \leq M$![]() . As $\operatorname {res}^M_{J_p}$
. As $\operatorname {res}^M_{J_p}$![]() is injective by induction, it follows that the composition $\operatorname {res}^J_{J_p} = \operatorname {res}^M_{J_p} \circ \operatorname {res}^J_M$
is injective by induction, it follows that the composition $\operatorname {res}^J_{J_p} = \operatorname {res}^M_{J_p} \circ \operatorname {res}^J_M$![]() is also injective. On the other hand,
is also injective. On the other hand,
where the equality above follows from the inductive hypothesis, so that $\operatorname {res}^J_{J_p}$![]() is surjective.
is surjective.
Otherwise, $q=p$![]() , so that $J_p=Q$
, so that $J_p=Q$![]() is a Sylow $p$
is a Sylow $p$![]() -subgroup of $J$
-subgroup of $J$![]() . In this case, $H^1(J/Q,\, N^Q)$
. In this case, $H^1(J/Q,\, N^Q)$![]() is trivial in (3.2) and so $\operatorname {res}^J_{J_p}$
is trivial in (3.2) and so $\operatorname {res}^J_{J_p}$![]() is injective. As $H^1(Q,\,N)^{J/Q} = \operatorname {inv}_J H^1(Q,\,N)$
is injective. As $H^1(Q,\,N)^{J/Q} = \operatorname {inv}_J H^1(Q,\,N)$![]() , it remains to show that this map is surjective. For $M$
, it remains to show that this map is surjective. For $M$![]() -invariant $\varphi \in Z^1(J_p,\, N)$
-invariant $\varphi \in Z^1(J_p,\, N)$![]() , define $\tilde \varphi : J \to N$
, define $\tilde \varphi : J \to N$![]() by $\tilde \varphi (hm) = \varphi (h)$
by $\tilde \varphi (hm) = \varphi (h)$![]() for $h\in J_p$
for $h\in J_p$![]() and $m\in M$
and $m\in M$![]() . Then for any $h,\,h' \in J_p$
. Then for any $h,\,h' \in J_p$![]() and $m,\, m' \in M$
and $m,\, m' \in M$![]() , we have $\tilde \varphi (hmh'm') = \varphi (h (h')^{m^{-1}}) = \varphi (h) \varphi ((h')^{m^{-1}})^{h^{-1}}$
, we have $\tilde \varphi (hmh'm') = \varphi (h (h')^{m^{-1}}) = \varphi (h) \varphi ((h')^{m^{-1}})^{h^{-1}}$![]() $= \varphi (h) \varphi (h')^{m^{-1}h^{-1}} = \tilde \varphi (hm) \tilde \varphi (h'm')^{(hm)^{-1}}$
$= \varphi (h) \varphi (h')^{m^{-1}h^{-1}} = \tilde \varphi (hm) \tilde \varphi (h'm')^{(hm)^{-1}}$![]() where the third equality follows from $\varphi$
where the third equality follows from $\varphi$![]() being $M$
being $M$![]() -invariant. As $J\cong J_p \rtimes M$
-invariant. As $J\cong J_p \rtimes M$![]() , we conclude that $\tilde \varphi \in Z^1(J,\, N)$
, we conclude that $\tilde \varphi \in Z^1(J,\, N)$![]() . Clearly, $\operatorname {res}^J_{J_p} \tilde \varphi \sim \varphi$
. Clearly, $\operatorname {res}^J_{J_p} \tilde \varphi \sim \varphi$![]() so that $\operatorname {res}^J_{J_p}$
so that $\operatorname {res}^J_{J_p}$![]() is surjective.
is surjective.
For each prime $p$![]() , we may apply proposition 3.1 to the component for $p$
, we may apply proposition 3.1 to the component for $p$![]() in (3.1) and find that $H^1(J,\,N_p)\cong \operatorname {inv}_J H^1(J_p,\, N_p) \cong \operatorname {inv}_J H^1(J_p,\, N)$
in (3.1) and find that $H^1(J,\,N_p)\cong \operatorname {inv}_J H^1(J_p,\, N_p) \cong \operatorname {inv}_J H^1(J_p,\, N)$![]() for some $J_p \in \operatorname {Syl}_p(J)$
for some $J_p \in \operatorname {Syl}_p(J)$![]() . In particular, it follows that:
. In particular, it follows that:
Proposition 3.2 Given a group $J$![]() acting on a nilpotent group $N$
acting on a nilpotent group $N$![]() via automorphisms so that $N\rtimes J$
via automorphisms so that $N\rtimes J$![]() is supersoluble, the restriction maps $\operatorname {res}^J_{J_p}$
is supersoluble, the restriction maps $\operatorname {res}^J_{J_p}$![]() induce an isomorphism of pointed sets $H^1(J,\, N) \cong \oplus _{p\in \mathcal {D}} \operatorname {inv}_J H^1(J_p,\, N)$
induce an isomorphism of pointed sets $H^1(J,\, N) \cong \oplus _{p\in \mathcal {D}} \operatorname {inv}_J H^1(J_p,\, N)$![]() where $\mathcal {D}$
where $\mathcal {D}$![]() denotes the set of prime divisors of $\lvert{J}\rvert$
denotes the set of prime divisors of $\lvert{J}\rvert$![]() and $J_p\in \operatorname {Syl}_p(J)$
and $J_p\in \operatorname {Syl}_p(J)$![]() for each $p\in \mathcal {D}$
for each $p\in \mathcal {D}$![]() .
.
We are now prepared to provide a proof of lemma 1.4.
Proof of lemma 1.4 In a supersoluble group $G$![]() , suppose $J$
, suppose $J$![]() and $J'$
and $J'$![]() are locally conjugate complements of a normal nilpotent subgroup $N$
are locally conjugate complements of a normal nilpotent subgroup $N$![]() . As in lemma 1.1, we have for each prime $p$
. As in lemma 1.1, we have for each prime $p$![]() that some $J_p\in \operatorname {Syl}_p(J)$
that some $J_p\in \operatorname {Syl}_p(J)$![]() and $J_p'\in \operatorname {Syl}_p(J')$
and $J_p'\in \operatorname {Syl}_p(J')$![]() are conjugate by an element of $N$
are conjugate by an element of $N$![]() . Let $\varphi '\in Z^1(J,\,N)$
. Let $\varphi '\in Z^1(J,\,N)$![]() denote the map corresponding to $J'$
denote the map corresponding to $J'$![]() . As the isomorphism in proposition 3.2 is induced by restriction maps, it takes the identity $1\in H^1(J,\, N)$
. As the isomorphism in proposition 3.2 is induced by restriction maps, it takes the identity $1\in H^1(J,\, N)$![]() to $\oplus _{p\in \mathcal {D}} 1|_{J_p}$
to $\oplus _{p\in \mathcal {D}} 1|_{J_p}$![]() . Thus, as $\varphi '|_{J_p}\sim 1|_{J_p}$
. Thus, as $\varphi '|_{J_p}\sim 1|_{J_p}$![]() for each $p\in \mathcal {D}$
for each $p\in \mathcal {D}$![]() , we may apply proposition 3.2 to conclude $\varphi '\sim 1$
, we may apply proposition 3.2 to conclude $\varphi '\sim 1$![]() so that $J$
so that $J$![]() and $J'$
and $J'$![]() are conjugate.
are conjugate.
We now use lemma 1.4 to show:
Proposition 3.3 Let $H$![]() be a subgroup of some supersoluble $G\cong N \rtimes J$
be a subgroup of some supersoluble $G\cong N \rtimes J$![]() where $N$
where $N$![]() is nilpotent. If for each prime $p$
is nilpotent. If for each prime $p$![]() , $H$
, $H$![]() contains a conjugate of some $S\in \operatorname {Syl}_p(J)$
contains a conjugate of some $S\in \operatorname {Syl}_p(J)$![]() , then $H$
, then $H$![]() contains a conjugate of $J$
contains a conjugate of $J$![]() and so splits over $N\cap H$
and so splits over $N\cap H$![]() .
.
Proof. The hypotheses imply that $H$![]() supplements $N$
supplements $N$![]() in $G$
in $G$![]() . We induct on the order of $G$
. We induct on the order of $G$![]() . If $N$
. If $N$![]() is trivial or if $H$
is trivial or if $H$![]() is a $p$
is a $p$![]() -group, the conclusion follows immediately. If multiple primes divide $\vert{N}\rvert$
-group, the conclusion follows immediately. If multiple primes divide $\vert{N}\rvert$![]() , then for some prime $p$
, then for some prime $p$![]() , $HN_p$
, $HN_p$![]() must be a strict subgroup of $G$
must be a strict subgroup of $G$![]() for $N_p \in \operatorname {Syl}_p(N)$
for $N_p \in \operatorname {Syl}_p(N)$![]() ; otherwise $H$
; otherwise $H$![]() would contain a Sylow subgroup of $G$
would contain a Sylow subgroup of $G$![]() for each prime and we would have $H=G$
for each prime and we would have $H=G$![]() . Let $p$
. Let $p$![]() be such a prime. Induction in $G/N_p$
be such a prime. Induction in $G/N_p$![]() implies $J^g \leq HN_p$
implies $J^g \leq HN_p$![]() for some $g\in G$
for some $g\in G$![]() . Switching to a conjugate of $H$
. Switching to a conjugate of $H$![]() if necessary, we may assume that $g$
if necessary, we may assume that $g$![]() is trivial and apply the inductive hypothesis in $HN_p$
is trivial and apply the inductive hypothesis in $HN_p$![]() to conclude $J^{g'} \leq H$
to conclude $J^{g'} \leq H$![]() for some $g'\in G$
for some $g'\in G$![]() . We now proceed under the assumption that $N$
. We now proceed under the assumption that $N$![]() is a $q$
is a $q$![]() -subgroup for some prime $q$
-subgroup for some prime $q$![]() .
.
Let $A \leq N$![]() be a minimal normal subgroup of $G$
be a minimal normal subgroup of $G$![]() ; as $G$
; as $G$![]() is supersoluble, it will have prime order $q$
is supersoluble, it will have prime order $q$![]() . If $A \leq H$
. If $A \leq H$![]() , then in $G/A$
, then in $G/A$![]() , induction implies that $J^gA \leq HA = H$
, induction implies that $J^gA \leq HA = H$![]() for some $g\in G$
for some $g\in G$![]() so that $J^g \leq H$
so that $J^g \leq H$![]() .
.
Otherwise, $A \cap H$![]() is trivial. Without loss, $J_q \leq H$
is trivial. Without loss, $J_q \leq H$![]() for some $J_q \in \operatorname {Syl}_q(J)$
for some $J_q \in \operatorname {Syl}_q(J)$![]() . In $G/A$
. In $G/A$![]() , induction implies that a conjugate of $JA/A$
, induction implies that a conjugate of $JA/A$![]() is contained in $HA/A$
is contained in $HA/A$![]() . Let $\overline {K}$
. Let $\overline {K}$![]() denote this conjugate. Switching to a different conjugate if necessary, we may assume that $J_qA/A \leq \overline {K}$
denote this conjugate. Switching to a different conjugate if necessary, we may assume that $J_qA/A \leq \overline {K}$![]() . Let $\varphi : h \mapsto hA/A$
. Let $\varphi : h \mapsto hA/A$![]() denote the isomorphism from $H$
denote the isomorphism from $H$![]() to $HA/A$
to $HA/A$![]() and consider $K = \varphi ^{-1}(\overline K)$
and consider $K = \varphi ^{-1}(\overline K)$![]() . It follows that $J_q \leq K$
. It follows that $J_q \leq K$![]() and $\vert{K}\rvert = \vert{J}\rvert$
and $\vert{K}\rvert = \vert{J}\rvert$![]() so that $K\leq H$
so that $K\leq H$![]() complements $N$
complements $N$![]() in $G$
in $G$![]() . As $N$
. As $N$![]() is a $q$
is a $q$![]() -group, a Sylow $p$
-group, a Sylow $p$![]() -subgroup of $J$
-subgroup of $J$![]() will be conjugate to a Sylow $p$
will be conjugate to a Sylow $p$![]() -subgroup of $K$
-subgroup of $K$![]() for primes $p\ne q$
for primes $p\ne q$![]() . Lemma 1.4 then implies that $J$
. Lemma 1.4 then implies that $J$![]() and $K\leq H$
and $K\leq H$![]() are conjugate in $G$
are conjugate in $G$![]() .
.
We now prove theorem 1.5.
Proof of theorem 1.5 Given $J$![]() , $N$
, $N$![]() , and $\Omega$
, and $\Omega$![]() as described in the hypotheses of the theorem, let $G= N \rtimes J$
as described in the hypotheses of the theorem, let $G= N \rtimes J$![]() denote the induced semidirect product and consider $G_\alpha$
denote the induced semidirect product and consider $G_\alpha$![]() for some $\alpha \in \Omega$
for some $\alpha \in \Omega$![]() . As $N$
. As $N$![]() acts transitively, $G=NG_\alpha$
acts transitively, $G=NG_\alpha$![]() . For each prime $p$
. For each prime $p$![]() , the hypotheses of the theorem imply $(J_p)^{n_p} \leq G_\alpha$
, the hypotheses of the theorem imply $(J_p)^{n_p} \leq G_\alpha$![]() for some $J_p \in \operatorname {Syl}_p(J)$
for some $J_p \in \operatorname {Syl}_p(J)$![]() and $n_p\in N$
and $n_p\in N$![]() , so that proposition 3.3 implies $G_\alpha$
, so that proposition 3.3 implies $G_\alpha$![]() contains a conjugate of $J$
contains a conjugate of $J$![]() , say $J^g$
, say $J^g$![]() for $g\in G$
for $g\in G$![]() . It follows that $J$
. It follows that $J$![]() fixes $\omega =g \cdot a$
fixes $\omega =g \cdot a$![]() .
.
This in turn implies:
Corollary 3.4 Let $G$![]() be a supersoluble split extension over a nilpotent subgroup $N$
be a supersoluble split extension over a nilpotent subgroup $N$![]() . If for each prime $p$
. If for each prime $p$![]() there is a Sylow $p$
there is a Sylow $p$![]() -subgroup $S$
-subgroup $S$![]() of $G$
of $G$![]() such that any two complements of $S\cap N$
such that any two complements of $S\cap N$![]() in $S$
in $S$![]() are conjugate, then any two complements of $N$
are conjugate, then any two complements of $N$![]() in $G$
in $G$![]() are conjugate.
are conjugate.
Proof. Suppose arbitrary $J$![]() and $J'$
and $J'$![]() complement $N$
complement $N$![]() in $G$
in $G$![]() . Then $G$
. Then $G$![]() acts on the cosets $\Omega = G/J'$
acts on the cosets $\Omega = G/J'$![]() in such a way that we may apply theorem 1.5 to infer that $J$
in such a way that we may apply theorem 1.5 to infer that $J$![]() fixes $gJ'$
fixes $gJ'$![]() for some $g\in G$
for some $g\in G$![]() . Consequently, $J$
. Consequently, $J$![]() and $J'$
and $J'$![]() are conjugate, and we may conclude.
are conjugate, and we may conclude.
4. Concluding remarks
In their paper, Losey and Stonehewer exhibited a soluble group $G\cong N \rtimes J$![]() with $N$
with $N$![]() nilpotent and $J$
nilpotent and $J$![]() supersoluble and a second complement $J'$
supersoluble and a second complement $J'$![]() to $N$
to $N$![]() in $G$
in $G$![]() such that $J$
such that $J$![]() and $J'$
and $J'$![]() are locally conjugate but not conjugate [Reference Losey and Stonehewer7]. Thus, lemma 1.4 cannot be extended to supersoluble complements of a normal nilpotent subgroup in a soluble group.
are locally conjugate but not conjugate [Reference Losey and Stonehewer7]. Thus, lemma 1.4 cannot be extended to supersoluble complements of a normal nilpotent subgroup in a soluble group.
Acknowledgements
The author thanks Elizabeth Crites, the editor Alex Bartel, and an anonymous reviewer for thoughtful and detailed feedback on the manuscript.