Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T12:51:36.013Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized Lambert series and arithmetic nature of odd zeta values

Part of: Zeta and $L$-functions: analytic theory Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  24 January 2019

Atul Dixit  and
Bibekananda Maji
Atul Dixit
Affiliation:
Discipline of Mathematics, Indian Institute of Technology Gandhinagar, Palaj, Gandhinagar382355, Gujarat, India (adixit@iitgn.ac.in; bibekananda.maji@iitgn.ac.in)
Bibekananda Maji
Affiliation:
Discipline of Mathematics, Indian Institute of Technology Gandhinagar, Palaj, Gandhinagar382355, Gujarat, India (adixit@iitgn.ac.in; bibekananda.maji@iitgn.ac.in)
Get access Rights & Permissions [Opens in a new window]

Abstract

It is pointed out that the generalized Lambert series 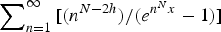$\sum\nolimits_{n = 1}^\infty {[(n^{N-2h})/(e^{n^Nx}-1)]} $ studied by Kanemitsu, Tanigawa and Yoshimoto can be found on page 332 of Ramanujan's Lost Notebook in a slightly more general form. We extend an important transformation of this series obtained by Kanemitsu, Tanigawa and Yoshimoto by removing restrictions on the parameters N and h that they impose. From our extension we deduce a beautiful new generalization of Ramanujan's famous formula for odd zeta values which, for N odd and m > 0, gives a relation between ζ(2m + 1) and ζ(2Nm + 1). A result complementary to the aforementioned generalization is obtained for any even N and m ∈ ℤ. It generalizes a transformation of Wigert and can be regarded as a formula for ζ(2m + 1 − 1/N). Applications of these transformations include a generalization of the transformation for the logarithm of Dedekind eta-function η(z), Zudilin- and Rivoal-type results on transcendence of certain values, and a transcendence criterion for Euler's constant γ.

Keywords

Lambert seriesDedekind eta functionodd zeta valuesEuler's constantRamanujan's formulatranscendence

MSC classification

Primary: 11M06: $zeta (s)$ and $L(s, chi)$
Secondary: 11J81: Transcendence (general theory)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 2 , April 2020 , pp. 741 - 769
Copyright
Copyright © Royal Society of Edinburgh 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Dedicated to Professor Bruce C. Berndt on account of his 80th birthday.

References

1Andrews, G.E. and Berndt, B.C.. Ramanujan's lost notebook, Part IV (New York: Springer-Verlag, 2013).CrossRefGoogle Scholar
2Apéry, R.. Irrationalité de ζ(2) et ζ(3). Astérisque 61 (1979), 11–13.Google Scholar
3Apéry, R.. Interpolation de fractions continues et irrationalité de certaines constantes, 37–63. Bull. Section des Sci., Tome III (Paris: Bibliothéque Nationale, 1981).Google Scholar
4Apostol, T.M.. Introduction to analytic number theory (New York: Springer-Verlag, 1998).Google Scholar
5Ball, K. and Rivoal, T.. Irrationalité d'une infinité de valeurs de la fonction zêta aux entiers impairs. (French), Invent. Math. 146 (2001), 193–207.CrossRefGoogle Scholar
6Berndt, B.C.. Modular transformations and generalizations of several formulae of Ramanujan. Rocky Mountain J. Math. 7 (1977), 147–189.CrossRefGoogle Scholar
7Berndt, B.C.. Ramanujan's notebooks, Part II (New York: Springer-Verlag, 1989).10.1007/978-1-4612-4530-8CrossRefGoogle Scholar
8Berndt, B.C.. Ramanujan's notebooks, Part III (New York: Springer-Verlag, 1991).CrossRefGoogle Scholar
9Berndt, B.C. and Straub, A.. On a secant Dirichlet series and Eichler integrals of Eisenstein series. Math. Z. 284 (2016), 827–852.10.1007/s00209-016-1675-0CrossRefGoogle Scholar
10Berndt, B.C. and Straub, A.. Ramanujan's formula for ζ(2n + 1), arXiv preprint arXiv:1701.02964, January 2017.Google Scholar
11Berndt, B.C., Dixit, A., Roy, A. and Zaharescu, A.. New pathways and connections in number theory and analysis motivated by two incorrect claims of Ramanujan. Adv. Math. 304 (2017), 809–929.CrossRefGoogle Scholar
12Chandrasekharan, K. and Narasimhan, R.. Hecke's functional equation and arithmetical identities. Ann. Math. 74 (1961), 1–23.CrossRefGoogle Scholar
13Conway, J.B.. Functions of one complex variable, 2nd edn (New York: Springer, 1978).CrossRefGoogle Scholar
14Dixit, A. and Maji, B.. On the generalized Lambert series $\sum\nolimits_{n = 1}^\infty {[(n^{N-(2h + 1)})/(e^{n^Nx}-1)]} $, in preparation.Google Scholar
15Erdös, P.. On arithmetical properties of Lambert series. J. Indian Math. Soc. (N. S.) 12 (1948), 63–66.Google Scholar
16Guinand, A.P.. Functional equations and self-reciprocal functions connected with Lambert series. Quart. J. Math. 15 (1944), 11–23.CrossRefGoogle Scholar
17Guinand, A.P.. Some rapidly convergent series for the Riemann ξ-function. Quart. J. Math. (Oxford) 6 (1955), 156–160.CrossRefGoogle Scholar
18Gun, S., Murty, M.R. and Rath, P.. Transcendental values of certain Eichler integrals. Bull. London Math. Soc. 43 (2011), 939–952.CrossRefGoogle Scholar
19Hančl, J. and Kristensen, S.. Metrical irrationality results related to values of the Riemann ζ-function, arXiv:1802.03946v1, February 12, 2018.Google Scholar
20Kanemitsu, S., Tanigawa, Y. and Yoshimoto, M.. On zeta- and L-function values at special rational arguments via the modular relation. In Proceeding of the International Conference on Special Functions and their Applications (Second Annual Conference) Vol. I. Lucknow, India (ed. Denis, R. Y. and Pathan, M. A.), February 2–4, pp. 21–42 (2001).Google Scholar
21Kanemitsu, S., Tanigawa, Y. and Yoshimoto, M.. On the values of the Riemann zeta-function at rational arguments. Hardy-Ramanujan J. 24 (2001), 11–19.Google Scholar
22Kanemitsu, S., Tanigawa, Y. and Yoshimoto, M.. On multiple Hurwitz zeta-function values at rational arguments. Acta Arith. 107, No. 1 (2003), 45–67.CrossRefGoogle Scholar
23Kanemitsu, S., Tanigawa, Y. and Yoshimoto, M.. On Dirichlet L-function values at rational arguments. Ramanujan Math. Soc. Lect. Notes, Ser. 1. 1 (2005), pp. 31–37.Google Scholar
24Katsurada, M.. On an asymptotic formula of Ramanujan for a certain theta-type series. Acta Arith. 97 (2001), 157–172.CrossRefGoogle Scholar
25Kirschenhofer, P. and Prodinger, H.. On some applications of formulae of Ramanujan in the analysis of algorithms. Mathematika 38 (1991), 14–33.CrossRefGoogle Scholar
26Lerch, M.. Sur la fonction ζ(s) pour valeurs impaires de l'argument. J. Sci. Math. Astron. pub. pelo Dr. F. Gomes Teixeira, Coimbra 14 (1901), 65–69.Google Scholar
27Luca, F. and Tachiya, Y.. Linear independence of certain Lambert series. Proc. Amer. Math. Soc. 142 (2014), 3411–3419.CrossRefGoogle Scholar
28Murty, M.R., Smyth, C. and Wang, R.J.. Zeros of Ramanujan polynomials. J. Ramanujan Math. Soc. 26 (2011), 107–125.Google Scholar
29Ramanujan, S.. On certain trigonometrical sums and their applications in the theory of numbers. Trans. Cambridge Philos. Soc. 22 (1918), 259–276.Google Scholar
30Ramanujan, S.. Collected papers of Srinivasa Ramanujan (New York, Chelsea, 1962).Google Scholar
31Ramanujan, S.. The lost notebook and other unpublished papers (New Delhi: Narosa, 1988).Google Scholar
32Ramanujan, S.. Notebooks (2 volumes), 2nd edn (Bombay: Tata Institute of Fundamental Research, 1957); 2012.Google Scholar
33Rivoal, T.. La fonction zêta de Riemann prend une infinité de valeurs irrationnelles aux entiers impairs. C. R. Acad. Sci. Paris Sér. I Math. 331 (2000), 267–270.CrossRefGoogle Scholar
34Wigert, S.. Sur une extension de la série de Lambert. Arkiv Mat. Astron. Fys. 19 (1925), 13 pp.Google Scholar
35Zudilin, W.W.. One of the numbers ζ(5), ζ(7), ζ(9) and ζ(11) is irrational. (Russian), Uspekhi Mat. Nauk 56 (2001), 149–150; translation in Russian Math. Surveys 56 No. 4 (2001), 774–776.Google Scholar