Article contents
Global existence and large time behaviour for the pressureless Euler–Naver–Stokes system in ℝ3
Published online by Cambridge University Press: 22 February 2023
Abstract
We investigate the global Cauchy problem for a two–phase flow model consisting of the pressureless Euler equations coupled with the isentropic compressible Navier–Stokes equations through a drag forcing term. This model was first derived by Choi–Kwon [J. Differential Equations, 261(1) (2016), pp. 654–711] by taking the hydrodynamic limit of the Vlasov/compressible Navier–Stokes equations. Under the assumption that the initial perturbation is sufficiently small, Choi–Kwon [J. Differential Equations, 261(1) (2016), pp. 654–711] established the global well–posedness and large time behaviour for the three dimensional periodic domain $\mathbb {T}^3$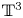 . However, up to now, the global well–posedness and large time behaviour for the three dimensional Cauchy problem still remain unsolved. In this paper, we resolve this problem by proving the global existence and optimal decay rates of classic solutions for the three dimensional Cauchy problem when the initial data is near its equilibrium. One of key observations here is that to overcome the difficulties arising from the absence of pressure in the Euler equations, we make full use of the drag forcing term and the dissipative structure of the Navier–Stokes equations to closure the energy estimates of the variables for the pressureless Euler equations.
. However, up to now, the global well–posedness and large time behaviour for the three dimensional Cauchy problem still remain unsolved. In this paper, we resolve this problem by proving the global existence and optimal decay rates of classic solutions for the three dimensional Cauchy problem when the initial data is near its equilibrium. One of key observations here is that to overcome the difficulties arising from the absence of pressure in the Euler equations, we make full use of the drag forcing term and the dissipative structure of the Navier–Stokes equations to closure the energy estimates of the variables for the pressureless Euler equations.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 154 , Issue 1 , February 2024 , pp. 328 - 352
- Copyright
- Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
- 5
- Cited by


