Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Vázquez, Juan Luis
and
Vitillaro, Enzo
2008.
Heat Equation with Dynamical Boundary Conditions of Reactive Type.
Communications in Partial Differential Equations,
Vol. 33,
Issue. 4,
p.
561.
Coclite, Giuseppe M.
Goldstein, Gisèle R.
and
Goldstein, Jerome A.
2008.
Stability estimates for parabolic problems with Wentzell boundary conditions.
Journal of Differential Equations,
Vol. 245,
Issue. 9,
p.
2595.
Coclite, Giuseppe M.
Goldstein, Gisèle R.
and
Goldstein, Jerome A.
2009.
Stability of parabolic problems with nonlinear Wentzell boundary conditions.
Journal of Differential Equations,
Vol. 246,
Issue. 6,
p.
2434.
Vitillaro, Enzo
and
Fiscella, Alessio
2013.
Local Hadamard well--posedness and blow--up for reaction--diffusion equations with non--linear dynamical boundary conditions.
Discrete and Continuous Dynamical Systems,
Vol. 33,
Issue. 11/12,
p.
5015.
Krasnoschok, Mykola
and
Vasylyeva, Nataliya
2013.
Existence and Uniqueness of the Solutions for Some Initial-Boundary Value Problems with the Fractional Dynamic Boundary Condition.
International Journal of Partial Differential Equations,
Vol. 2013,
Issue. ,
p.
1.
Vitillaro, Enzo
2014.
James Serrin. Selected Papers.
p.
283.
Fila, Marek
Ishige, Kazuhiro
Kawakami, Tatsuki
and
Lankeit, Johannes
2019.
Rate of convergence in the large diffusion limit for the heat equation with a dynamical boundary condition.
Asymptotic Analysis,
Vol. 114,
Issue. 1-2,
p.
37.
Zhang, Hongwei
Hu, Qingying
and
Liu, Gongwei
2020.
Global existence, asymptotic stability and blow‐up of solutions for the generalized Boussinesq equation with nonlinear boundary condition.
Mathematische Nachrichten,
Vol. 293,
Issue. 2,
p.
386.
Zhang, Mingyou
Zhao, Qingsong
Liu, Yu
and
Li, Wenke
2020.
Finite time blow-up and global existence of solutions for semilinear parabolic equations with nonlinear dynamical boundary condition.
Electronic Research Archive,
Vol. 28,
Issue. 1,
p.
369.
Fila, Marek
Ishige, Kazuhiro
and
Kawakami, Tatsuki
2021.
The large diffusion limit for the heat equation with a dynamical boundary condition.
Communications in Contemporary Mathematics,
Vol. 23,
Issue. 01,
p.
2050003.
Sun, Fenglong
Wang, Yutai
and
Yin, Hongjian
2022.
Blow-up problems for a parabolic equation coupled with superlinear source and local linear boundary dissipation.
Journal of Mathematical Analysis and Applications,
Vol. 514,
Issue. 2,
p.
126327.
Fila, Marek
Ishige, Kazuhiro
and
Kawakami, Tatsuki
2023.
Solvability of the heat equation on a half-space with a dynamical boundary condition and unbounded initial data.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 74,
Issue. 4,
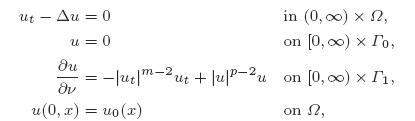 where Ω ⊂ Rn (n ≥ 1) is a regular and bounded domain, ∂Ω = Γ0 ∪ Γ1, m > 1, 2 ≤ p < r, where r = 2(n − 1)/(n − 2) when n ≥ 3, r = ∞ when n = 1, 2 and u0 ∈ H1(Ω), u0 = 0 on Γ0. We prove local existence of the solutions in H1(Ω) when m > r/(r + 1−p) or n = 1, 2 and global existence when p ≤ m or the initial datum is inside the potential well associated to the stationary problem.
where Ω ⊂ Rn (n ≥ 1) is a regular and bounded domain, ∂Ω = Γ0 ∪ Γ1, m > 1, 2 ≤ p < r, where r = 2(n − 1)/(n − 2) when n ≥ 3, r = ∞ when n = 1, 2 and u0 ∈ H1(Ω), u0 = 0 on Γ0. We prove local existence of the solutions in H1(Ω) when m > r/(r + 1−p) or n = 1, 2 and global existence when p ≤ m or the initial datum is inside the potential well associated to the stationary problem.

