Article contents
Heteroclinic orbits between rotating waves in hyperbolic balance laws
Published online by Cambridge University Press: 14 November 2011
Abstract
We deal with the large-time behaviour of scalar hyperbolic conservation laws with source terms
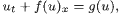
which are often called hyperbolic balance laws. Fan and Hale have proved existence of a global attractor 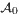 for this equation with x ∈ S1.
for this equation with x ∈ S1. 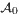 consists of spatially homogeneous equilibria, a large number of rotating waves and of heteroclinic orbits between these objects. In this paper, we solve the connection problem and show which equilibria and rotating waves are connected by a heteroclinic orbit. Apart from existence results, our approach via generalized characteristics also gives geometric information about the heteroclinic solutions, e.g. about the shock curves and their strength.
consists of spatially homogeneous equilibria, a large number of rotating waves and of heteroclinic orbits between these objects. In this paper, we solve the connection problem and show which equilibria and rotating waves are connected by a heteroclinic orbit. Apart from existence results, our approach via generalized characteristics also gives geometric information about the heteroclinic solutions, e.g. about the shock curves and their strength.
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 129 , Issue 3 , 1999 , pp. 519 - 538
- Copyright
- Copyright © Royal Society of Edinburgh 1999
References
- 9
- Cited by

