Homogenization of the spectral problem on the Riemannian manifold consisting of two domains connected by many tubes
Published online by Cambridge University Press: 03 December 2013
Abstract
The paper deals with the asymptotic behaviour as ε → 0 of the spectrum of the Laplace–Beltrami operator Δε on the Riemannian manifold Mε (dim Mε = N ≥ 2) depending on a small parameter ε > 0. Mε consists of two perforated domains, which are connected by an array of tubes of length qε. Each perforated domain is obtained by removing from the fixed domain Ω ⊂ ℝN the system of ε-periodically distributed balls of radius dε = ō(ε). We obtain a variety of homogenized spectral problems in Ω; their type depends on some relations between ε, dε and qε. In particular, if the limits
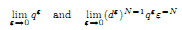
are positive, then the homogenized spectral problem contains the spectral parameter in a nonlinear manner, and its spectrum has a sequence of accumulation points.
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 143 , Issue 6 , December 2013 , pp. 1255 - 1289
- Copyright
- Copyright © Royal Society of Edinburgh 2013
- 4
- Cited by

