No CrossRef data available.
Published online by Cambridge University Press: 14 November 2011
We study the bifurcation of limit cycles in general quadratic perturbations of the particular quadratic system 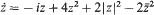 which represents one of two codimension-five components in the intersection of two strata in the centre manifold,
which represents one of two codimension-five components in the intersection of two strata in the centre manifold, 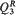 and Q4. The study of limit cycles for this degenerate case requires us to investigate not the first but the second variation M2 of the displacement function. We prove that up to three limit cycles can emerge from the period annulus surrounding the centre. This implies that the cyclicity of period annuli of nearby systems in
and Q4. The study of limit cycles for this degenerate case requires us to investigate not the first but the second variation M2 of the displacement function. We prove that up to three limit cycles can emerge from the period annulus surrounding the centre. This implies that the cyclicity of period annuli of nearby systems in 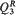 and Q4 is at most three as well. Our approach relies upon the possibility of deriving appropriate Picard–Fuchs equations satisfied by the four independent integrals included in M2.
and Q4 is at most three as well. Our approach relies upon the possibility of deriving appropriate Picard–Fuchs equations satisfied by the four independent integrals included in M2.