Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chen, Bang-Yen
1997.
Interaction of Legendre curves and Lagrangian submanifolds.
Israel Journal of Mathematics,
Vol. 99,
Issue. 1,
p.
69.
Chen, Bang-yen
1997.
Complex extensors and Lagrangian submanifolds in complex Euclidean spaces.
Tohoku Mathematical Journal,
Vol. 49,
Issue. 2,
Chen, Bang-Yen
2000.
Vol. 1,
Issue. ,
p.
187.
Castro, Ildefonso
and
Vrancken, Luc
2001.
Minimal Lagrangian submanifolds in ℂP 3 and the sinh-Gordon equation.
Results in Mathematics,
Vol. 40,
Issue. 1-4,
p.
130.
Castro, Ildefonso
Montealegre, Cristina R.
and
Urbano, Francisco
2001.
Closed conformal vector fields and Lagrangian submanifolds in complex space forms.
Pacific Journal of Mathematics,
Vol. 199,
Issue. 2,
p.
269.
Li, Haizhong
and
Vrancken, Luc
2005.
A basic inequality and new characterization of Whitney spheres in a complex space form.
Israel Journal of Mathematics,
Vol. 146,
Issue. 1,
p.
223.
Chen, Bang-Yen
2005.
An Optimal Inequality and Extremal Classes of Affine Spheres in Centroaffine Geometry.
Geometriae Dedicata,
Vol. 111,
Issue. 1,
p.
187.
Chen, Bang-Yen
2010.
Lagrangian submanifolds in para-Kähler manifolds.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 73,
Issue. 11,
p.
3561.
Tripathi, Mukut Mani
2011.
Improved Chen–Ricci inequality for curvature-like tensors and its applications.
Differential Geometry and its Applications,
Vol. 29,
Issue. 5,
p.
685.
Mihai, Ion
2017.
Topics in Modern Differential Geometry.
p.
223.
Sun, Jun
and
Sun, Linlin
2020.
Sphere theorems for Lagrangian and Legendrian submanifolds.
Calculus of Variations and Partial Differential Equations,
Vol. 59,
Issue. 4,
Hu, Zejun
and
Yin, Jiabin
2020.
An Optimal Inequality Related to Characterizations of the Contact Whitney Spheres in Sasakian Space Forms.
The Journal of Geometric Analysis,
Vol. 30,
Issue. 4,
p.
3373.
Zhao, Entao
and
Cao, Shunjuan
2022.
Characterization of Whitney spheres among Lagrangian submanifolds with conformal Maslov form.
Differential Geometry and its Applications,
Vol. 84,
Issue. ,
p.
101902.
Mihai, Adela
and
Mihai, Ion
2022.
Contact Geometry of Slant Submanifolds.
p.
39.
Luo, Yong
and
Yin, Jiabin
2022.
On energy gap phenomena of the Whitney sphere and related problems.
Pacific Journal of Mathematics,
Vol. 320,
Issue. 2,
p.
299.
Sasahara, Toru
2022.
Special Slant Surfaces with Non-constant Mean Curvature in 2-Dimensional Complex Space Forms.
Results in Mathematics,
Vol. 77,
Issue. 5,
Hu, Zejun
and
Xing, Cheng
2022.
New Characterizations of the Whitney Spheres and the Contact Whitney Spheres.
Mediterranean Journal of Mathematics,
Vol. 19,
Issue. 2,
Luo, Yong
and
Zhang, Liuyang
2023.
On Energy Gap Phenomena of the Whitney Spheres in ℂn or ℂℙn.
Chinese Annals of Mathematics, Series B,
Vol. 44,
Issue. 4,
p.
599.
Xing, Cheng
and
Yin, Jiabin
2024.
Some Optimal Inequalities for Anti-invariant Submanifolds of the Unit Sphere.
The Journal of Geometric Analysis,
Vol. 34,
Issue. 2,
Mihai, Ion
and
Olteanu, Andreea
2024.
Chen-like Inequalities for Submanifolds in Kähler Manifolds Admitting Semi-Symmetric Non-Metric Connections.
Symmetry,
Vol. 16,
Issue. 10,
p.
1401.
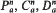 and two exceptional Lagrangian submanifolds Fn, Ln in nonflat complex-space-forms which satisfy the equality case of the inequality. Finally, we obtain the complete classification of Lagrangian submanifolds in nonflat complex-space-forms which satisfy this basic equality.
and two exceptional Lagrangian submanifolds Fn, Ln in nonflat complex-space-forms which satisfy the equality case of the inequality. Finally, we obtain the complete classification of Lagrangian submanifolds in nonflat complex-space-forms which satisfy this basic equality.

