Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T00:55:25.116Z Has data issue: false hasContentIssue false
  • English
  • Français

Least energy solution for a scalar field equation with a singular nonlinearity

Published online by Cambridge University Press:  24 January 2020

Jaeyoung Byeon ,
Sun-Ho Choi ,
Yeonho Kim  and
Sang-Hyuck Moon
Jaeyoung Byeon
Affiliation:
Department of Mathematical Sciences, KAIST, Daejeon34141, Republic of Korea (byeon@kaist.ac.kr)
Sun-Ho Choi
Affiliation:
Department of Applied Mathematics and Institute of Natural Sciences, Kyung Hee University, Yongin17104, Republic of Korea (sunhochoi@khu.ac.kr)
Yeonho Kim
Affiliation:
Department of Mathematical Sciences, KAIST, Daejeon34141, Republic of Korea (yho0922@kaist.ac.kr)
Sang-Hyuck Moon
Affiliation:
National Center for Theoretical Sciences, National Taiwan University, Taipei10617, Taiwan (shmoon@ncts.ntu.edu.tw)
Get access Rights & Permissions [Opens in a new window]

Abstract

We are concerned with a nonnegative solution to the scalar field equation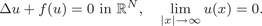

$$\Delta u + f(u) = 0{\rm in }{\open R}^N,\quad \mathop {\lim }\limits_{|x|\to \infty } u(x) = 0.$$
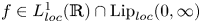A classical existence result by Berestycki and Lions [3] considers only the case when f is continuous. In this paper, we are interested in the existence of a solution when f is singular. For a singular nonlinearity f, Gazzola, Serrin and Tang [8] proved an existence result when $f \in L^1_{loc}(\mathbb {R}) \cap \mathrm {Lip}_{loc}(0,\infty )$ with 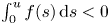$\int _0^u f(s)\,{\rm d}s < 0$ for small 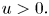$u>0.$ Since they use a shooting argument for their proof, they require the property that 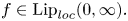$f \in \mathrm {Lip}_{loc}(0,\infty ).$ In this paper, using a purely variational method, we extend the previous existence results for 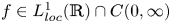$f \in L^1_{loc}(\mathbb {R}) \cap C(0,\infty )$. We show that a solution obtained through minimization has the least energy among all radially symmetric weak solutions. Moreover, we describe a general condition under which a least energy solution has compact support.

Keywords

Least energy solutionscalar field equationsingular nonlinearitycompact supported solution
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 1 , February 2021 , pp. 93 - 109
Check for updates
Copyright
Copyright © Royal Society of Edinburgh 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Acciaio, B., and Pucci, P.. Existence of radial solutions for quasilinear elliptic equations with singular nonlinearities. Adv. Nonlinear Stud. 3 (2003), 511–539.CrossRefGoogle Scholar
2Berestycki, H., Gallouet, T. and Kavian, O.. Équations de champs scalaires euclidiens non linaires dans le plan. Compt. Rend. Acad. Sci. 297 (1983), 307–310.Google Scholar
3Berestycki, H. and Lions, P.-L.. Nonlinear scalar field equations, I. Existence of a ground state. Arch. Rational Mech. Anal. 82 (1983), 313–345.CrossRefGoogle Scholar
4Byeon, J., Jeanjean, L. and Maris, M.. Symmetry and monotonicity of least energy solutions. Calc. Var. Partial Differ. Equ. 36 (2009), 481–492.CrossRefGoogle Scholar
5Chung, J., Kim, Y.-J., Kwon, O. and Pan, X., Discontinuous nonlinearity and finite time extinction, submitted.Google Scholar
6Cortázar, C., Elgueta, M. and Felmer, P.. Symmetry in an elliptic problem and the blow-up set of a quasilinear heat equatio. Comm. Partial Differ. Equ. 21 (1996), 507–520.CrossRefGoogle Scholar
7Davila, J. and Montenegro, M.. Concentration for an elliptic equation with singular nonlinearity. J. Math. Pures Appl. 97 (2012), 545–578.CrossRefGoogle Scholar
8Gazzola, F., Serrin, J. and Tang, M.. Existence of ground states and free boundary problems for quasilinear elliptic operators. Adv. Differ. Equ. 5 (2000), 1–30.Google Scholar
9Gilbarg, D. and Trudinger, N. S.. Elliptic Partial Differential Equations of Second Order, 2nd ed., 224 (Berlin: Springer-Verlag, 1983).Google Scholar
10Gui, C.. Symmetry of the blow-up set of a porous medium type equation. Comm. Pure Appl. Math. 48 (1995), 471–500.CrossRefGoogle Scholar
11Kaper, H. G., Kwong, M. K. and Li, Y.. Symmetry results for reaction-diffusion equations. Differ. Int. Equ. 6 (1993), 1045–1056.Google Scholar
12Pohožaev, S. I.. On the eigenfunctions of the equation $\Delta u + \lambda f(u) = 0$. Dokl. Akad. Nauk SSSR 61 (1965), 36–39.Google Scholar
13Pucci, P., Garcia-Huidobro, M., Manasevich, R. and Serrin, J.. Qualitative properties of ground states for singular elliptic equations with weights. Ann. Mat. Pura Appl. 185 (2006), S205–S243.CrossRefGoogle Scholar
14Pucci, P., Serrin, J. and Zou, H.. A strong maximum principle and a compact support principle for singular elliptic inequalities. J. Math. Pures Appl. 78 (1999), 769–789.CrossRefGoogle Scholar
15Redheffer, R.. Nonlinear differential inequalities and functions of compact support. Trans. Amer. Math. Soc. 220 (1976), 133–157.CrossRefGoogle Scholar
16Serrin, J. and Tang, M.. Uniqueness of ground states for quasilinear elliptic equations. Indiana Univ. Math. J. 49 (2000), 897–923.CrossRefGoogle Scholar
17Vázquez, J. L.. A strong maximum principle for some quasilinear elliptic equations. Appl. Math. Optim. 3 (1984), 191–202.CrossRefGoogle Scholar