No CrossRef data available.
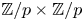 on $S^{2n-1}\times S^{2n-1}$
on $S^{2n-1}\times S^{2n-1}$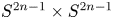
Published online by Cambridge University Press: 16 April 2024
For an odd prime $p$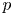 , we consider free actions of $(\mathbb {Z}_{/{p}})^2$
, we consider free actions of $(\mathbb {Z}_{/{p}})^2$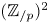 on $S^{2n-1}\times S^{2n-1}$
on $S^{2n-1}\times S^{2n-1}$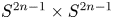 given by linear actions of $(\mathbb {Z}_{/{p}})^2$
given by linear actions of $(\mathbb {Z}_{/{p}})^2$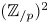 on $\mathbb {R}^{4n}$
on $\mathbb {R}^{4n}$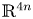 . Simple examples include a lens space cross a lens space, but $k$
. Simple examples include a lens space cross a lens space, but $k$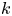 -invariant calculations show that other quotients exist. Using the tools of Postnikov towers and surgery theory, the quotients are classified up to homotopy by the $k$
-invariant calculations show that other quotients exist. Using the tools of Postnikov towers and surgery theory, the quotients are classified up to homotopy by the $k$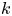 -invariants and up to homeomorphism by the Pontrjagin classes. We will present these results and demonstrate how to calculate the $k$
-invariants and up to homeomorphism by the Pontrjagin classes. We will present these results and demonstrate how to calculate the $k$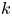 -invariants and the Pontrjagin classes from the rotation numbers.
-invariants and the Pontrjagin classes from the rotation numbers.