Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-02-08T15:29:47.015Z Has data issue: false hasContentIssue false
  • English
  • Français

Linearized stability implies dynamic stability for equilibria of 1-dimensional, p-Laplacian boundary value problems

Part of: Parabolic equations and systems Partial differential equations

Published online by Cambridge University Press:  29 January 2019

Bryan P. Rynne
Bryan P. Rynne*
Affiliation:
Department of Mathematics and the Maxwell Institute for Mathematical Sciences, Heriot-Watt University, Edinburgh, EH14 4AS, Scotland (B.P.Rynne@hw.ac.uk)
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the parabolic, initial-boundary value problem 1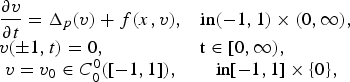

$$\matrix{ {\displaystyle{{\partial v} \over {\partial t}} = \Delta _p(v) + f(x,v),} & {{\rm in}({\rm - 1},{\rm 1}) \times ({\rm 0},\infty ),} \cr {v( \pm 1,t) = 0,} \hfill \hfill \hfill & {{\rm t}\in [{\rm 0},\infty ),} \hfill \hfill \cr {v = v_0\in C_0^0 ([-1,1]),} & {{\rm in}[{\rm - 1},{\rm 1}] \times \{ {\rm 0}\} ,} \cr } $$
where Δp denotes the p-Laplacian on ( − 1, 1), with p > 1, and the function f:[ − 1, 1] × ℝ → ℝ is continuous, and the partial derivative fv exists and is continuous and bounded on [ − 1, 1] × ℝ. It will be shown that (under certain additional hypotheses) the ‘principle of linearized stability’ holds for equilibrium solutions u0 of (1). That is, the asymptotic stability, or instability, of u0 is determined by the sign of the principal eigenvalue of a suitable linearization of the problem (1) at u0. It is well-known that this principle holds for the semilinear case p = 2 (Δ2 is the linear Laplacian), but has not been shown to hold when p ≠ 2.

We also consider a bifurcation type problem similar to (1), having a line of trivial solutions. We characterize the stability or instability of the trivial solutions, and the bifurcating, non-trivial solutions, and show that there is an ‘exchange of stability’ at the bifurcation point, analogous to the well-known result when p = 2.

Keywords

p-Laplacianparabolic boundary value problemstabilitybifurcation

MSC classification

Primary: 35K55: Nonlinear parabolic equations
Secondary: 35B35: Stability 35B32: Bifurcation
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 3 , June 2020 , pp. 1313 - 1338
Copyright
Copyright © 2019 The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Afrouzi, G. A. and Rasouli, S. H.. A Remark on the linearized stability of positive solutions for systems involving the p-Laplacian. Positivity 11 (2007), 351–356.CrossRefGoogle Scholar
2Akagi, G. and Otani, M.. Evolution inclusions governed by subdifferentials in reflexive Banach spaces. J. Evol. Equ. 4 (2004), 519–541.CrossRefGoogle Scholar
3Atkinson, F. V.. Discrete and continuous boundary problems (New York: Academic Press, 1964).Google Scholar
4Binding, P. and Drábek, P.. Sturm-Liouville theory for the p-Laplacian. Studia Sci. Math. Hungar. 40 (2003), 375–396.Google Scholar
5Binding, P. A. and Rynne, B. P.. The spectrum of the periodic p-Laplacian. J. Differ. Equ. 235 (2007), 199–218.CrossRefGoogle Scholar
6Cantrell, R. S. and Cosner, C.. Upper and lower solutions for a homogeneous Dirichlet problem with nonlinear diffusion and the principle of linearized stability. Rocky Mountain J. Math. 30 (2000), 1229–1236.CrossRefGoogle Scholar
7Chill, R. and Fiorenza, A.. Convergence and decay rate to equilibrium of bounded solutions of quasilinear parabolic equations. J. Differ. Equ. 228 (2006), 611–632.CrossRefGoogle Scholar
8Crandall, M. G. and Rabinowitz, P. H. Bifurcation from simple eigenvalues. J. Func. Anal. 8 (1971), 321–340.CrossRefGoogle Scholar
9Crandall, M. G. and Rabinowitz, P. H. Bifurcation, perturbation of simple eigenvalues and linearized stability. Arch. Rational Mech. Anal. 52 (1973), 161–180.CrossRefGoogle Scholar
10DiBenedetto, E.. Degenerate parabolic equations (New York: Springer, 1993).CrossRefGoogle Scholar
11Garcia-Melian, J. and Sabina de Lis, J.. A local bifurcation theorem for degenerate elliptic equations with radial symmetry. J. Differ. Equ. 179 (2002), 27–43.CrossRefGoogle Scholar
12Genoud, F.. Bifurcation along curves for the p-Laplacian with radial symmetry. Electron. J. Differ. Equ. 124 (2012), 1–17.Google Scholar
13Hess, P.. On bifurcation and stability of positive solutions of nonlinear elliptic eigenvalue problems. In Dynamical systems, II (Gainesville, Fla., 1981), pp. 103–119 (New York: Academic Press, 1982).Google Scholar
14Huang, Y.-X. and Metzen, G.. The existence of solutions to a class of semilinear differential equations. Differ. Integral. Equ. 8 (1995), 429–452.Google Scholar
15Karatson, J. and Simon, P. L.. On the linearised stability of positive solutions of quasilinear problems with p-convex or p-concave nonlinearity. Nonlinear Anal. 47 (2001), 4513–4520.CrossRefGoogle Scholar
16Li, Y. and Xie, C.. Blow-up for p-Laplacian parabolic equations. Electron. J. Differ. Equ. 20 (2003), 1–12.Google Scholar
17Renardy, M. and Rogers, R. C.. An introduction to partial differential equations (New York: Springer, 1993).Google Scholar
18Rynne, B. P.. Simple bifurcation and global curves of solutions of p-Laplacian problems with radial symmetry. J. Differ. Equ. 263 (2017), 3611–3626.CrossRefGoogle Scholar
19Zhao, J. N.. Existence and nonexistence of solutions for $u_t = {\rm div} (\vert \nabla \vert^{p - 2}\nabla u) + f(\nabla u,u,x,t)$. J. Math. Anal. Appl. 172 (1993), 130–146.CrossRefGoogle Scholar