Hostname: page-component-5b777bbd6c-4n89n Total loading time: 0 Render date: 2025-06-22T23:11:25.341Z Has data issue: false hasContentIssue false
  • English
  • Français

Local linear independence of refinable vectors of functions

Published online by Cambridge University Press:  11 July 2007

T. N. T. Goodman ,
R.-Q. Jia  and
D.-X. Zhou
T. N. T. Goodman
Affiliation:
Department of Mathematics, University of Dundee, Dundee DD1 4HN, UK (tgoodman@mcs.dundee.ac.uk)
R.-Q. Jia
Affiliation:
Department of Mathematical Sciences, University of Alberta, Edmonton, Canada T6G 2G1 (jia@xihu.math.ualberta.ca)
D.-X. Zhou
Affiliation:
Department of Mathematics, City University of Hong Kong, Kowloon, Hong Kong (mazhou@math.cityu.edu.hk)
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is devoted to a study of local linear independence of refinable vectors of functions. A vector of functions 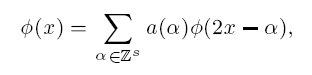is said to be refinable if it satisfies the vector refinement equation where a is a finitely supported sequence of r × r matrices called the refinement mask. A complete characterization for the local linear independence of the shifts of ϕ1,…,ϕr is given strictly in terms of the mask. Several examples are provided to illustrate the general theory. This investigation is important for construction of wavelets on bounded domains and nonlinear approximation by wavelets.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 130 , Issue 4 , August 2000 , pp. 813 - 826
Copyright
Copyright © Royal Society of Edinburgh 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable