Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Amar, Micol
Bellettini, Giovanni
and
Venturini, Sergio
1998.
Integral representation of functionals defined on curves ofW1,p.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 128,
Issue. 2,
p.
193.
Ceragioli, Francesca
2002.
Some remarks on stabilization by means of discontinuous feedbacks.
Systems & Control Letters,
Vol. 45,
Issue. 4,
p.
271.
2008.
Discontinuous dynamical systems.
IEEE Control Systems,
Vol. 28,
Issue. 3,
p.
36.

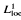 -convergence for the differential inclusion
-convergence for the differential inclusion