Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Godefroy, G.
2014.
Obituary: Nigel John Kalton, 1946–2010.
Bulletin of the London Mathematical Society,
Vol. 46,
Issue. 6,
p.
1292.

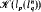 is the only nontrivial
is the only nontrivial 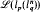 .
.