Minimal energy for geometrically nonlinear elastic inclusions in two dimensions

Abstract

We are concerned with a variant of the isoperimetric problem, which in our setting arises in a geometrically nonlinear two-well problem in elasticity. More precisely, we investigate the optimal scaling of the energy of an elastic inclusion of a fixed volume for which the energy is determined by a surface and an (anisotropic) elastic contribution. Following ideas from Conti and Schweizer (Commun. Pure Appl. Math. 59 (2006), 830–868) and Knüpfer and Kohn (Proc. R. Soc. London Ser. A Math. Phys. Eng. Sci. 467 (2011), 695–717), we derive the lower scaling bound by invoking a two-well rigidity argument and a covering result. The upper bound follows from a well-known construction for a lens-shaped elastic inclusion.

1. Introduction

This article is concerned with a variant of the isoperimetric problem, for which we investigate the optimal energy of an elastic inclusion of a fixed volume. Here the energy consists of an interfacial and a geometrically nonlinear elastic contribution. The latter is defined by an integral of the stored-energy density function over a domain. As usual, the stored-energy density depends on the strain and describes properties of the material. Physically, the problem is motivated by nucleation phenomena which arise, for instance, in shape-memory materials [9].

The set-up considered in this work is the geometrically nonlinear analogue of [42] where the isoperimetric problem for a geometrically linear elastic two-phase inclusion problem had been investigated. Our main aim is to deduce quantitative information on the nucleation problem by studying its scaling properties. The problem of determining the sharp form of the inclusion seems to be more complicated [60]. In addition to the presence of non-quasiconvexity as in [42], in the geometrically nonlinear setting under investigation, an additional difficulty is present in the form of the nonlinear gauge group ${\rm SO}(2)$. We emphasize that nonlinear models are more general than linear ones and, therefore, should be considered primarily. Linearized elasticity correctly describes only very particular deformations that are close to elastic equilibria (cf. [8] for a comparison of the two theories). In order to deal with the nonlinear structure of the model, we hence rely on the geometrically nonlinear rigidity result from [28] in combination with the ideas from [42].

1.1 Model and statement of results

We consider the interior nucleation of a new phase in an elastic material in two space dimensions. More specifically, we consider a material for which two different phases (lattice structures) are energetically preferred. These are represented by the ${\rm SO}(2)$ orbit of the identity matrix $\operatorname {Id} \in \mathbb {R}^{2 \times 2}$ and the ${\rm SO}(2)$ orbit of another matrix $F \in \mathbb {R}^{2 \times 2}\backslash {\rm SO}(2)$. The deformation of the material is described by a function $v : \mathbb {R}^2 \to \mathbb {R}^2$. By the Cauchy–Born rule the energy of an elastic material can be represented in terms of the gradient of the deformation function $v$. Following the phenomenological theory of martensite and assuming Hooke's law, we study (volume-constrained) minimizers of the energy

(1.1)\begin{equation} {\mathcal{E}}[\chi, v] = \int_{\mathbb{R}^2} |\nabla \chi| + \int_{\mathbb{R}^2} (1 - \chi) {\rm dist}^2(\nabla v,{\rm SO}(2)) + \chi {\rm dist}^2(\nabla v,{\rm SO}(2)F) . \end{equation}

Here $\chi : \mathbb {R}^2 \rightarrow \{ 0 , 1 \}$ encodes the location of the new, minority phase. Its variation i.e. the first integral in (1.1) is the interfacial energy, while the second integral is the elastic energy. Hence, our model includes penalizations of transitions between the phases and deviations from the corresponding material phase. We introduce $\mu >0$ to denote the volume of the inclusion

(1.2)\begin{equation} \mu = \int_{\mathbb{R}^2} \chi \end{equation}

for the region $M:=\{x\in \mathbb {R}^2: \ \chi (x)=1\}$ associated with the minority phase. In what follows, we will consider minimizers of the energy (1.1) for a prescribed volume of the minority phase. In order to rule out self-intersections, as the set ${\mathcal {A}}_m$ of admissible functions we consider

\begin{align*} {\mathcal{A}}_m & := \ \left\{ (\chi, v) \in BV(\mathbb{R}^2, \{ 0, 1 \}) \times H_{\rm loc}^1(\mathbb{R}^2, \mathbb{R}^2): \right.\\ & \left. \qquad \quad v \text{ is bi-Lipschitz } \text{with constant } m \geq 1\right\}. \end{align*}

Here bi-Lipschitz with constant $m\geq 1$ means that $v$ is a homeomorphism and $v$ and $v^{-1}$ are Lipschitz continuous functions with Lipschitz constants $m\geq 1$. Seeking to model nucleation phenomena, we assume that the strain $F$ is compatible with the identity matrix. In two dimensions this is equivalent to the condition $\det F = 1$. Our main result is the scaling of the minimal energy for prescribed inclusion volume:

Theorem 1.1 (Scaling of ground-state energy)

Suppose that $F \in \mathbb {R}^{2 \times 2}\backslash {\rm SO}(2)$ satisfies $\det F = 1$. Let $\mu$ be as in (1.2). Let $m \geq \max \{ \|F\|_{}, \|F^{-1}\|_{} \} + C$ for some sufficiently large constant $C>0$. Then for any $\mu >0$ we have

\[ \inf_{(\chi,v) \in {\mathcal{A}}_m\ \text{satisfies}\ (1.2)} {\mathcal{E}}[\chi, v] \sim \left\{ \begin{array}{@{}ll@{}} \mu^{{1}/{2}} & \text{ for } \mu\leq 1,\\ \mu^{{2}/{3}} & \text{ for } \mu\geq 1. \end{array} \right. \]

Here, we write $A \sim B$ by which we mean that $cA \leq B \leq CB$ for two constants $c,C > 0$ which are independent of $\mu$ but may depend on $F$. The first bound in Theorem 1.1 corresponds to the usual isoperimetric regime in which the surface energy dominates while the second estimate for $\mu \geq 1$ captures the effect of the interaction of the surface and elastic energies. In particular, the role of anisotropy in the elastic contribution in the form of the two physical phenomena of compatibility and self-accommodation are captured in it. We do not track the dependence on $\| F\|$ in the energy scaling behaviour.

The result of theorem 1.1 confirms the similar scalings which had been obtained in the framework of piecewise linear elasticity in [42]. In particular, the result shows that in the framework of geometrically nonlinear elasticity, the model imposes enough rigidity to ensure the same lower bound on the energy as in the geometrically linear model. This is in line with the fact that the only solution for the two-gradient problem for two compatible strains are twins in nonlinear elasticity theory [3, proposition 2] as well as in linear elasticity theory. If we allow for more variants of martensite, the situation is expected to become more intricate since in this case the corresponding many gradient problems possibly allow for a large number of non-trivial solutions and complicated microstructure [9, 60].

1.2 Ideas of the proof

The proof of our main result can be split into two parts: an ansatz-free lower-bound estimate and an upper-bound construction.

On the one hand, in order to verify the lower bound, we observe that without loss of generality, we may assume the deformation $F$ to be symmetric and positive-definite after using the polar decomposition theorem. By a suitable choice of coordinates, $F$ hence takes the form

\[ F = \begin{pmatrix} \lambda & 0\\ 0 & \frac{1}{\lambda} \end{pmatrix} \quad \text{for some }0<\lambda < 1. \]

With these normalization results on hand, in the small volume regime, the lower bound follows by the standard isoperimetric inequality. In the large volume setting, we deduce the lower bound by a combination of a segment rigidity argument from [28] (§ 2) and the localization argument from [42] (§ 4.1). Working with phase indicator energies as in [42] or [13], see (1.1), contrary to the energies in [28], we do not directly control the full second derivatives of the deformation $v$. This additional degeneracy results in a number of small adaptations becoming necessary. For settings with full second-derivative control the key localized energy estimate in proposition 3.1 would directly follow from corollary 2.5 in [28]. Moreover, in this case also the higher-dimensional problem could be treated directly in parallel by invoking the results from [19] or [37]. With our energies this would require adaptations of these strategies, e.g. in the associated rigidity results, which we do not pursue in the present article. The slightly stronger degeneracy of our energy which does not immediately yield the full second-derivative control, also accounts for one of the technical reasons for our bi-Lipschitz assumptions in the minimization problem; another reason being the use of approximation theory for bi-Lipschitz functions in § 3. Although more general deformations might be possibly considered at the expense of various technical difficulties, we would like to emphasize that bi-Lipschitz deformations automatically guarantee injectivity everywhere, that is essential in mathematical elasticity. Results ensuring almost everywhere injectivity rely on Hölder continuous deformations and orientation-preserving maps [23]. Additional control of the distortion is needed if we want to achieve injectivity everywhere [36].

On the other hand, the upper bound is derived by constructing a deformation $v$ corresponding to a well-known construction for a lens-shaped elastic inclusion (see e.g. [42]) which in our geometrically nonlinear setting leads to an orientation-preserving deformation.

1.3 Relation to the literature

Due to their physical significance and the intrinsic mathematical interest in ‘non-isotropic’ isoperimetric inequalities, nucleation problems for shape-memory materials have been studied in various settings: in a geometrically linearized framework the compatible and incompatible two-well problems (one variant of martensite and one variant of austenite) have been considered in [42], where a localization strategy was introduced. This also forms one of the two core ingredients of our result. Moreover, the nucleation behaviour for the geometrically linearized cubic-to-tetragonal phase transformation was studied in [43] in which Fourier theoretic arguments in the spirit of [12, 13] were exploited. Fourier theoretic arguments also underlie the study of the nucleation of multiple phases without gauge invariance in [65]. Using related ideas, the nucleation behaviour at corners of martensite in an austenite matrix was investigated in [6]. We also refer to [4, 5, 53] for the study of quasiconvexity at the boundary. Further, highly symmetric, low-energy nucleation mechanisms have been explored in [16, 27] both in the geometrically linear and nonlinear theories in two dimensions. In the geometrically nonlinear settings substantially less is known in terms of nucleation properties due to the presence of the nonlinear gauge group. In this context, the incompatible two-well problem was studied in [18] in which an incompatible two-well analogue of the Friesecke–James–Müller rigidity result [35] was used. Moreover, the study of model singular perturbation problems for the analysis of austenite–martensite interfaces in terms of a surface energy parameter [49, 50] laid the basis for an intensive, closely related research on singular perturbation problems for shape-memory alloys [17, 20, 21, 24, 28, 29, 31, 56, 63, 64, 66, 68]. Contrary to the full nucleation problems, in these settings the phenomenon of compatibility plays the main role, while nucleation phenomena in addition require the analysis of the phenomenon of self-accommodation. Moreover, dynamic nucleation results have been considered in [32, 33, 54]. We refer to [55, 60] for further references on these and related results.

Nonlocal isoperimetric inequalities have also been investigated for the Ohta–Kawasaki energy and related models with Riesz interaction. For example, we refer to [1, 10, 11, 34, 38, 39, 45, 46, 57]. In these models, above a critical volume minimizers do not exist anymore and the scaling of the energy in terms of the mass is linear. Other related vectorial models where the energy includes both interface type energies as well as a (dipolar) nonlocal interaction are ferromagnetic systems. The nucleation of magnetic domains during magnetization reversal and corresponding optimal magnetization patterns have been investigated in [44, 47, 48], see also [61]. The competition between a nonlocal repulsive potential and an attractive confining term is found also in other problems, for example in models studying the interaction of dislocations [41, 67] or [14, 15, 59]. Another anisotropic and nonlocal repulsive energy that has been treated variationally using ansatz-free analysis is discussed in [15] (based on [14, 59]). We finally briefly mention investigations of other physical settings where related nonlocal isoperimetric inequalities have been studied. This includes the works [51, 52, 62] on compliance minimization, on epitaxial growth (e.g. [7]), on dislocations (e.g. [25]) and superconductors (e.g. [22, 26]). We emphasize that the above list of references is far from exhaustive.

1.4 Notation

We write $A \lesssim B$ if $A \leq C B$ for some constant $C$ which is independent of $\mu$, but may, for instance, depend on $F$. The Frobenius norm of a matrix $A\in \mathbb {R}^{d\times l}$ is denoted by $\|A\|=\sqrt {\operatorname {tr}(A^tA)}$. For two matrices $A,B$ we write ${\rm dist}(A,B) := \|A-B\|_{}$, where $\|\cdot \|_{}$ is the Frobenius norm, analogously, we define ${\rm dist}(A,{\mathcal {K}}) := {\rm dist}_{K \in {\mathcal {K}}}(A,K)$ for any ${\mathcal {K}} \subset \mathbb {R}^{2 \times 2}$.

By $B_R(x)$ we denote the ball of radius $R>0$ centred at $x \in \mathbb {R}^2$ and we write $B_R := B_R(0)$. We write $M:={\rm spt}\,\chi \subset \mathbb {R}^2$ to denote the support of the minority phase. For $E\subset \mathbb {R}^2$ and $v \in BV(E)$, the total variation of $v$ is denoted by $\|\nabla v\|_E$.

2. Rigidity

The aim of this section is to find a ‘good’ set in the shape of a rhombus which fulfils a variant of the rigidity estimate from [28]. We first introduce some notation for the elastic energies for the deformation $v$. We set

\[ e_{\rm elast}(\chi,v) \ : = \ (1 - \chi) {\rm dist}^2(\nabla v,{\rm SO}(2)) + \chi {\rm dist}^2(\nabla v,{\rm SO}(2)F). \]

Then the elastic energy for a one-dimensional (1D) or two-dimensional subset $E \subset \mathbb {R}^2$ is defined as

(2.1)\begin{equation} {\mathcal{E}}_{\rm elast}[\chi, v,E] := \int_{E} e_{\rm elast}(\chi,v) \end{equation}

and the total elastic energy is ${\mathcal {E}}_{\rm elast}[\chi, v] := {\mathcal {E}}_{\rm elast}[\chi, v,\mathbb {R}^2]$. Similarly, we introduce

\[ {\mathcal{E}}_{\rm elast}'[\chi, v,E] := \int_{E} (1 - \chi) {\rm dist}^2(\nabla v,{\rm SO}(2)) + \chi {\rm dist}^2(\nabla v,{\rm SO}(2)F^{{-}1}), \]

which we will use in order to deal with estimates for the inverse of $v$. If the subset is 1D we integrate over the 1D Hausdorff measure instead of the Lebesgue measure.

Before stating the central rigidity estimate, we formulate two auxiliary lemmas. First, we note that there is a large set of non-singular points:

Lemma 2.1 (Non-singular points)

Let $f \in L^1(B_R)$ and $R>0$. Then for any $\theta > 0$ there is $U \subset B_R$ with $|B_R \backslash {U}| < \theta$ and a constant $C = C(\theta )>0$ such that for any $x_0 \in U$ we have

\[ \int_{B_R} |f(x)| \frac{1}{{\rm dist}{(x,x_0)}}\,{\rm d}x \leq\ \frac{C}{ R} \ {\|f\|_{L^{1}(B_R)}}. \]

Proof. This follows by an application of Fubini's theorem and since ${\rm dist}^{-1}{(\cdot,x_0)} \in L_{\rm loc}^1$.

By our bi-Lipschitz assumption, bounds on $v$ can be translated into analogous bounds for its inverse:

Lemma 2.2 Let $R>0$, $m\geq 1$ and let $(\chi, v)\in {\mathcal {A}}_m$ with $v(0)=0$ and $v\in C^1(B_{mR})$. Assume that

\[ {\|\chi\|_{L^{1}(B_{mR})}} \leq \eta R^2 \ \text{and}\ \|\nabla \chi\|_{B_{mR}} \quad \leq\ \eta R. \]

Then for $\chi _1 :=\chi \circ (v^{-1})$ we have

1. (i) $\displaystyle {\|\chi _1\|_{L^{1}(B_{R})}} \leq m^2 \eta R^2;$

2. (ii) $\displaystyle \|\nabla (\chi _1)\|_{B_{R}} \leq m \eta R;$

3. (iii) $\displaystyle {\mathcal {E}}'_{\rm elast}[\chi _1, v^{-1}, B_R] \leq C {\mathcal {E}}_{\rm elast}[\chi, v, B_{mR}]$ for some constant $C=C(m, F)>0$.

Proof. By the transformation formula and since $v \in {\mathcal {A}}_m$, (i) follows from

\[ \|\chi_1\|_{L^1(B_R)} \leq\int_{B_{mR}}\chi(y)|\det \nabla v(y)|\,{\rm d}y \leq\ m^2{\|\chi\|_{L^{1}(B_{mR})}}\leq m^2\eta R^2. \]

By the chain rule for BV functions (cf. theorem 3.16 in [2]) this implies

\[ \int_{B_{R}}|\nabla \chi_1| \leq\ m \int_{B_{mR}}|\nabla \chi| = m\eta R. \]

The claim of (iii) follows by an application of the linear algebra fact from lemma A.2(ii). Indeed, using the pointwise identity

(2.2)\begin{equation} {\rm dist}^2((\nabla v)^{{-}1},{\rm SO}(2) A^{{-}1}) \leq\ C {\rm dist}^2(\nabla v,{\rm SO}(2) A) \quad \text{for}\ A \in \{ \operatorname{Id}, F \} \end{equation}

together with the inverse function theorem, the transformation theorem and with the notation $\tilde v := v^{-1}$, we arrive at

\begin{align*} {\mathcal{E}}'_{\rm elast}[\chi_1, \tilde v, B_R] & = \int_{B_R} (1 - \chi_1(y)) {\rm dist}^2((\nabla v)_{|\tilde v(y)}^{{-}1},{\rm SO}(2))\\ & \quad + \chi_1(y) {\rm dist}^2((\nabla v)_{|\tilde v(y)}^{{-}1},{\rm SO}(2) F^{{-}1})\,{\rm d}y \\ & \stackrel{(2.2)}{\leq\ } \ C \int_{B_{mR}}(1 - \chi(x)) {\rm dist}^2(\nabla v(x),{\rm SO}(2))\\ & \quad + \chi(x) {\rm dist}^2(\nabla v(x),{\rm SO}(2) F)\,{\rm d}x\\ & = C {\mathcal{E}}_{\rm elast}[\chi, v, B_{mR}] \end{align*}

for some constant $C=C(m, F)>0$. This completes the proof.

We are now ready to give the key rigidity estimate. It is a variant of the two-well rigidity estimate from [28] and shows that we can find a sufficiently large rhombus such that we control the energy and the change of length on all six connecting lines between the corner points of this rhombus both for the transformation and its inverse:

Lemma 2.3 (Rigidity estimate): Let $R>0$, $m\geq 1$, $\delta \in (0, R/{m})$. Then there are constants $\eta =\eta (\delta )>0$ and $C = C(\delta,m,F)>0$ such that the following holds: assume $(\chi, v)\in {\mathcal {A}}_m$ satisfies $v\in C^1(\overline {B_R},\mathbb {R}^2)$,

(2.3)\begin{equation} {\|\chi\|_{L^{1}(B_R)}} \leq \eta R^2\ \text{and}\ \|\nabla \chi\|_{B_R} \leq \eta R. \end{equation}

Then there exist four points ${\mathcal {C}} := \{ a, b, c, d \} \subset B_{{R}/{m}}\subset \mathbb {R}^2$ with $|a-b| \sim R/m$ and $|c-d| \sim \delta R/m$, which form the end-points of a symmetric rhombus $T$ such that for all $x,y\in {\mathcal {C}}$ and with the notation $M = spt\, \chi$ we have the following properties:

1. (i) $\displaystyle [x, y] \cap M = \emptyset$;

2. (ii) $\displaystyle {\mathcal {E}}_{\rm elast}[\chi,v,[x, y]] \leq \ \frac {C}{R} {\mathcal {E}}_{\rm elast}[\chi, v,B_R]$;

3. (iii) $\displaystyle \int _{B_R} e_{\rm {elast}}(\chi, v) \frac {{\rm d}z}{{\rm dist}(z,x)} \leq \frac {C}{R} {\mathcal {E}}_{\rm elast}[\chi, v, B_R]$.

Furthermore, for $\chi _1 :=\chi \circ (v^{-1})$ we have

1. (iv) $\displaystyle [v(x), v(y)] \cap v(M) = \emptyset$;

2. (v) $\displaystyle {\mathcal {E}}_{\rm elast}'[\chi _1,v^{-1},[v(x), v(y)]] \leq \frac {C}{R} {\mathcal {E}}_{\rm elast}'[\chi _1, v^{-1},B_R]$;

3. (vi) there exist $Q\in {\rm SO}(2)$ and $p\in \mathbb {R}^2$ such that

   \[ |v(x)-Qx-p|\leq C({\mathcal{E}}_{\rm elast}[\chi, v, B_R]^{1/2}+\eta^{1/2}). \]

   Finally, we have rigidity on all six segments

4. (vii) $\displaystyle \left | 1 - \frac {|v(x)-v(y)|}{|x-y|} \right | \leq \ \frac {C}{R} {\mathcal {E}}_{\rm elast}[\chi, v, B_R]^{ 1/2}$.

Proof. Without loss of generality, by scaling, we may assume that $R=m$ and $v(0)=0$. We further choose $\theta \in (0,1)$ sufficiently small to be determined below. We argue in several steps based on averaging-type arguments.

Step 1: Identification of a symmetric cross satisfying (i) and (ii). We first construct horizontal and vertical segments forming a ‘cross’ satisfying (i) and (ii). For $\delta \in (0, 1/2)$ and $r \in (-\delta, \delta )$ we define the horizontal line segment by $L_{\rm hor}(r) =[p_{-}(r),p_+(r)] \subset B_1$ where $p_{\pm }(r):=(\pm 1/2,r)$. We first show that if $\eta >0$ is sufficiently small, there exists a subset $E \subset (-\delta,\delta )$ of volume fraction $1-\theta$ such that

\[ L_{\rm hor}(r)\cap M = \emptyset\ \text{and}\ {\mathcal{E}}_{\rm elast}[\chi,v, L_{\rm hor}(r)] \leq C{\mathcal{E}}_{\rm elast}[\chi, v, B_1] \text{ for all } r\in E. \]

Indeed, for some $C=C(\delta, \theta )>0$, we define

\[ E \ := \left\{ r\in (-\delta,\delta): {\|\chi\|_{L^{1}(L_{\rm hor}(r))}} + \|\nabla \chi\|_{L_{\rm hor}(r)} \leq \theta \text{ and } \frac{{\mathcal{E}}_{\rm elast}[\chi,v, L_{\rm hor}(r)]}{{\mathcal{E}}_{\rm elast}[\chi, v, B_1]} \leq C \right\}. \]

By Chebyshev's inequality and in view of (2.3) we have

\[ |(-\delta,\delta)\backslash E|\leq\ \frac{\eta}{\theta} + \frac{1}{C} \leq\ (2\delta) \theta \]

by choosing $\eta = \eta (\delta,\theta )$ sufficiently small and $C = C(\delta,\theta )$ sufficiently large. In particular, $|E| \geq 2\delta (1-\theta )$. Now, since for each $r\in E$, $\nabla \chi |_{L_{\rm hor}(r)}$ is a discrete measure and since $\theta \in (0, 1)$, this implies $\nabla \chi |_{L_{\rm hor}(r)} = 0$ for all $r\in E$. By definition of $E$ we then have $\chi _{|L_{\rm hor}(r)} = 0$ for $r \in E$ (cf. [42, p. 701]). This shows that outside of volume fraction $\theta$, the horizontal segments $L_{\rm hor}(r)$ have properties (i)–(ii).

Next, we repeat this argument along the vertical lines of the form $L_{\rm ver}(s)=[q_{-}(s),q_+(s)]$ with $q_{\pm }(s)=(s,\pm \delta )$ for $s\in [-1/2, 1/2]$. Also for this set, we analogously find a volume fraction $\tilde {E}\subset [-1/2,1/2]$ of size $1-\theta$ such that these vertical line segments satisfy (i)–(ii).

Consider now the sets $\{L_{\rm hor}(r)\}_{r\in E}$ and $\{L_{\rm ver}(s)\}_{s\in \tilde {E}}$ of all horizontal and vertical segments with properties (i)–(ii), respectively (see figure 1). Let $o(s,r) =L_{\rm hor}(r) \cap L_{\rm ver}(s)$ be the intersection point of the corresponding horizontal and vertical line. The point $o(s,r)$ divides both $L_{\rm hor}(r)$ and $L_{\rm ver}(s)$ into two segments denoted by $L_{\rm hor}^+(r)$ and $L_{\rm hor}^-(r)$ (also $L_{\rm ver}^+(s)$ and $L_{\rm ver}^-(s)$). Since $E$ and $\tilde {E}$ are sets of positive (close to one) volume fractions, there exist $r_0\in E$ and $s_0\in \tilde {E}$ such that $|L_{\rm hor}^+(r_0)|\sim |L_{\rm hor}^-(r_0)|$ and $|L_{\rm ver}^+(s_0)|\sim |L_{\rm ver}^-(s_0)|$. Consequently, we choose $L_{\rm hor}'$ and $L_{\rm ver}'$ such that $o=L_{\rm hor}(r_0)\cap L_{\rm ver}(s_0)$ is the midpoint of $L_{\rm hor}'$ as well as the midpoint of $L_{\rm ver}'$. This can be done by (if necessary) cutting exceeding parts of $L_{\rm hor}(r_0)$ and $L_{\rm ver}(s_0)$; we note that such a modification preserves the conditions $|L_{\rm hor}'|\sim 1$ and $|L_{\rm ver}'|\sim \delta$.

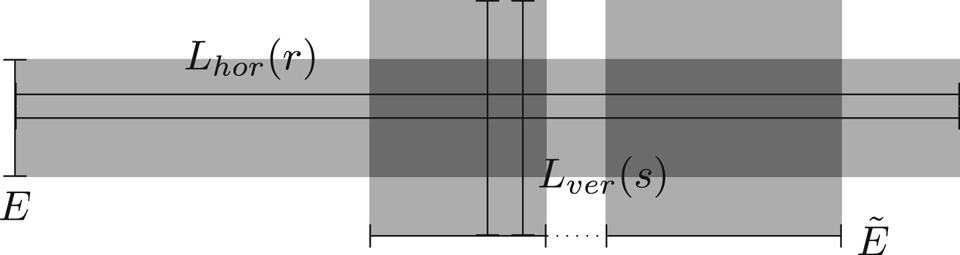
Figure 1. Grey rectangles represent sets of horizontal and vertical segments with properties (i)–(ii).

Step 2: Identification of a ‘good’ rhombus. Let $L_{\rm hor}'$ and $L_{\rm ver}'$ be the segments forming a symmetric cross and satisfying (i)–(ii) as in the previous step. Let $\hat T$ be the symmetric rhombus given by the convex hull of this cross. We denote by $\hat {T}_\rho$ the homothetically shrunken rhombus with the self-similarity factor $\rho \in (0,1]$ and the same centre point. For $\rho \in ({1}/{4},{3}/{4})=:I$, the diagonals (given by the corresponding shortened line segments of the originally constructed cross) of the resulting symmetric rhombi $\hat T_\rho$ also satisfy (i)–(ii) by construction, see figure 2. After using a Fubini argument as in step 1, we obtain a subset $I_1$ of $I$ on which all sides of the rhombus fulfil properties (i)–(ii).

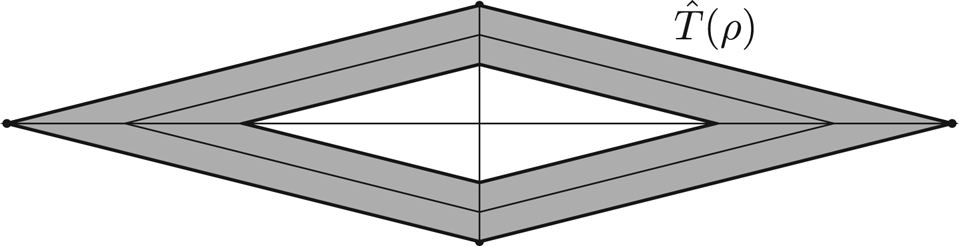
Figure 2. Sketch of a set of rhombi $\hat {T}(\rho )$, $\rho \in ({1}/{4},{3}/{4})$.

Next, we seek to ensure that properties (iii)–(v) are also satisfied on the edges of some of these rhombi. Invoking lemma 2.1 together with another averaging argument, we obtain another set $I_2\subset I$ of positive volume fraction satisfying (iii). In addition to this, since $v$ is bi-Lipschitz and by lemma 2.2(i)–(ii), we can repeat step 1 with the functions $v^{-1}$ and $\chi _1$, the energy ${\mathcal {E}}'_{\rm elast}[\chi _1,v^{-1},B_m]$ and for the line segments $[v(x),v(y)]$, where $x,y$ form the endpoints of the rhombi $\hat T_\rho$ for $\rho \in I$. Thus, noting that by the bi-Lipschitz property of $v$, the length of the lines $[v(x),v(y)]$ is (up to a factor $m, m^{-1}$) comparable to that of $[x,y]$ and after possibly enlarging the constant $C>0$, we obtain a subset $I_3$ of $I$ with properties (iv)–(v). By choosing the intersection of these subsets of $I$, we arrive at a subset of $I$ with positive volume fraction such that all sides of $\hat {T}_{\rho }$ fulfil (i)–(v) for $\rho$ in this subset, provided $\eta >0$ is sufficiently small.

By the Friesecke–James–Müller rigidity theorem [35] and Poincaré's inequality, there exist $Q\in {\rm SO}(2)$ and $p\in \mathbb {R}^2$ such that for constants $C_{\delta }, C_{F}>0$, we have

\begin{align*} \|v(x)-Qx - p \|_{L^2(\hat{T}_\rho)}^{ 2} & \leq\ C_\delta \|\nabla v - Q\|_{L^2(\hat{T}_\rho)}^{ 2} \leq C_\delta \| {\rm dist}(\nabla v, {\rm SO}(2)) \|_{L^2(\hat{T}_\rho)}^{2}\\ & \leq\ C_\delta({\mathcal{E}}_{\rm elast}[\chi, v, B_m] + {\rm dist}({\rm SO}(2)F, {\rm SO}(2)) |\hat{T}_\rho\cap M|) \\ & \leq\ C_\delta({\mathcal{E}}_{\rm elast}[\chi, v, B_m] + C_F\eta). \end{align*}

Again, the use of a Fubini argument implies that there are many values of $\rho$ such that the resulting rhombi $\hat {T}_\rho$ are ‘good’, in the sense that all lines connecting the corner points of the rhombus satisfy properties (i)–(v) and that for some constant $C=C(F,\delta )>0$ we have

\[ \|v(x)-(Qx+p)\|_{L^2(\partial \hat{T}_\rho)}^{ 2}+\|\nabla v-Q\|_{L^2(\partial\hat{T}_\rho)}^{ 2} \ \leq C({\mathcal{E}}_{\rm elast}[\chi, v, B_m]+\eta). \]

Then by Sobolev's embedding theorem, we obtain

(2.4)\begin{equation} \|v(x)-(Qx+p)\|_{L^\infty(\partial \hat{T}_\rho)}^{ 2} \leq\ C({\mathcal{E}}_{\rm elast}[\chi, v, B_m]+\eta). \end{equation}

We choose one such ‘good’ rhombus and denote it by $T$ and define its endpoints as the points ${\mathcal {C}} := \{ a,b,c,d \}$ (see figure 3). Since $v$ is a continuous function, we obtain from inequality (2.4)

\[ |v(x)-(Qx+p)|^{ 2} \leq C({\mathcal{E}}_{\rm elast}[\chi, v, B_m]+\eta) \quad\text{for }x\in {\mathcal{C}}. \]

As a consequence, by construction properties (i)–(vi) are satisfied for these endpoints.

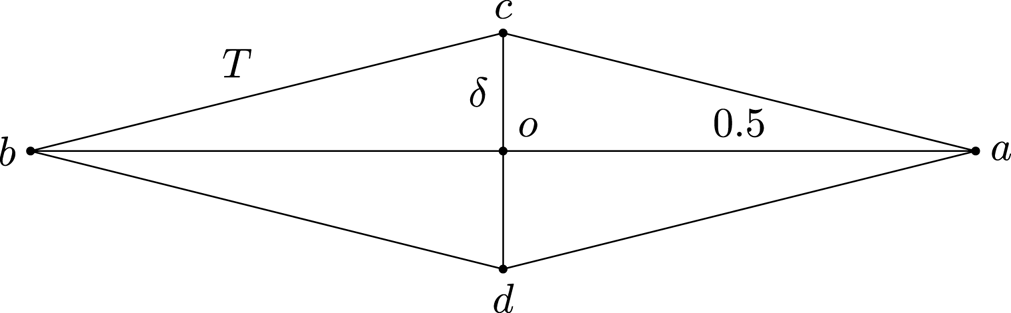
Figure 3. Sketch of the rhombus $T$ constructed in lemma 2.3.

Step 3: Proof of (vii). By the fundamental theorem of calculus, for any $x,y \in {\mathcal {C}}$ we have

(2.5)\begin{align} |v(x)-v(y)| & \leq\ \int_{[x,y]} |\nabla v| \leq\ |x-y| + \int_{[x,y]} {\rm dist}(\nabla v,{\rm SO}(2))\nonumber\\ & \stackrel{(ii)}{ \leq } \ |x-y| + C {\mathcal{E}}_{\rm elast}[\chi,v,B_1]^{1/2}. \end{align}

Now, we apply the same argument to $v^{-1}(v(x))-v^{-1}(v(y))$ with $x,y \in {\mathcal {C}}$. Thus, in view of lemma 2.2, for a constant $C=C(\delta, m, F)>0$ we obtain

(2.6)\begin{align} |x-y| & \leq\ \int_{[v(x),v(y)]} |\nabla v^{{-}1}(z)| \nonumber\\ & \leq\ |v(x)- v(y)| + \int_{[v(x),v(y)]} {\rm dist}(\nabla (v^{{-}1}),{\rm SO}(2)) \nonumber\\ & \stackrel{(iv),(v)}{\leq} |v(x)- v(y)|+C{\mathcal{E}}_{\rm elast}'[\chi_1, v^{{-}1},B_1]^{ 1/2}\nonumber\\ & \leq |v(x)- v(y)|+C{\mathcal{E}}_{\rm elast}[\chi, v,B_m]^{1/2}. \end{align}

Combining inequalities (2.5) and (2.6), we obtain the desired estimate (vii). This completes the proof of the lemma.

3. A lower bound for the elastic energy

In this section, we prove a local lower bound by exploiting the rigidity argument from lemma 2.3 and the ideas from the proof of lemma 2.3 in [28]. This local lower bound provides a geometrically nonlinear variant of the central lower bound from proposition 3.1 in [42]. In § 4.1 we will combine it with a covering argument as in [42] which will imply the lower bound of theorem 1.1.

Proposition 3.1 (Lower bound on elastic energy)

There is $\eta > 0$ such that for any $R > 0$ the following holds: suppose that $(\chi, v)\in {\mathcal {A}}_m$ satisfies

\[ {\|\chi\|_{L^{1}(B_R)}} \leq \eta R^2 \text{ and }\|\nabla \chi\|_{B_R} \leq \eta R. \]

Then there are constants $\alpha = \alpha (m) \in (0,1)$ and $C = C(F,\alpha,m)>0$ such that

(3.1)\begin{equation} {\mathcal{E}}_{\rm elast}[\chi,v,B_R] \geq \frac {C}{R^2} \|\chi\|_{L^1(B_{\alpha R})}^2. \end{equation}

Proof. This result essentially follows from an application of a variant of the two-well rigidity result from [28]. Here there are slight adaptations in steps 1 and 2 in the proof due to the choice of our energies (full gradient control in [28] vs. our phase-indicator energies), while steps 3 and 4 then follow essentially without changes as in [28]. For self-containedness, we repeat the argument for proposition 3.1.

By scaling we can assume $R=m$ and by the approximation results in [30] for bi-Lipschitz functions we can further assume that $v \in C^1(\overline {B_m})$.

Following the argument in [28] in our proof we will construct a rhombus $T$ with $B_\alpha \subset T \subset B_1$ and show that the corresponding estimate (3.1) holds for $T$ replaced by $B_\alpha$ for some $\alpha > 0$. We write $\mu := {\|\chi \|_{L^{1}(B_{\alpha })}}$ and $\epsilon := {\mathcal {E}}_{\rm elast}[\chi,v,B_m]$. Moreover, we note that, without loss of generality, we can assume

(3.2)\begin{equation} \epsilon^{1/2} < \eta. \end{equation}

Indeed, if $\epsilon$ is large e.g. $\epsilon ^{1/2}\geq \eta$, then by assumption we have $\|\chi \|_{L^1(B_1)}\leq \eta \leq \epsilon ^{1/2}$. Then inequality (3.1) follows immediately.

Step 1: Construction of a ‘good’ rhombus. Since $F \neq \operatorname {Id}$ and $\det F = 1$ after a rotation of coordinates, we may assume that $|Fe_1|<1$. Hence, there exists $\delta >0$ such that

\[ |F\xi|<1-2\delta\quad\text{for all }\xi\in\mathbb{R}^2 \quad\text{with }|\xi|=1 \text{ such that }|\xi-e_1|<2\delta. \]

Without loss of generality we can assume that $\delta \in (0, 1)$ so that the conditions of lemma 2.3 with $R = m$ are satisfied. We then consider a rhombus $T$ with corner points ${\mathcal {C}} := \{ a, b, c, d \}$ as obtained in lemma 2.3, see figure 3. Since $|c-d|\sim \delta$ and $|a-b| \sim 1$, in particular,

(3.3)\begin{equation} |F(p-t)| < |p -t|(1 -\delta) \quad \text{ for all } p \in \{ a, b \}, t \in [c,d]. \end{equation}

By lemma 2.3 we further have properties (i)–(vii) for this rhombus.

Step 2: We claim that there exist $Q\in {\rm SO}(2)$ and $p \in \mathbb {R}^2$ such that $v(x)$ is close to $Q x + p$ for any point $x\in {\mathcal {C}}$ up to an error of order $\epsilon ^{1/2}$. Indeed, by lemma 2.3(vii) the six lengths $|x-y|$ for $x,y\in {\mathcal {C}}$ are preserved by $v$ up to errors of order $\varepsilon ^{ 1/2}$. This implies that there are two isometries $x\to Q_j x + p_j$ with $Q_j \in \text {O}(2)$, $p_j\in \mathbb {R}^2$ and $j\in \{1,2\}$ such that for the constant $C=C(\delta,m,F)>0$ from lemma 2.3 we have

\begin{align*} & |v(x)-(Q_1 x+p_1 )| \leq C\epsilon^{ 1/2}\quad\text{for }x\in\{b,c,d\} \text{ and } \\ & |v(x)-(Q_2 x+p_2 )| \leq C\epsilon^{ 1/2}\quad\text{for }x\in\{a,c,d\}. \end{align*}

It remains to argue that $Q_1, Q_2 \in {\rm SO}(2)$ and $p_1, p_2 \in \mathbb {R}^2$ can be chosen to be equal, respectively.

We first argue that $Q_j \in {\rm SO}(2)$. In [28] this follows from the second-gradient control and the pointwise estimates in the endpoints of the rhombus. Lacking the control of the full gradient, we here vary the argument slightly. The use of lemma 2.3(vi) and the triangle inequality implies that for some constant $C = C(F,\delta,m)>0$ and for $Q\in {\rm SO}(2)$, $p\in \mathbb {R}^2$ we have

\[ |Qx+p-(Q_1x+p_1)|\leq C (\epsilon^{1/2}+\eta^{1/2})\text{ for }x\in\{b,c,d\}. \]

For $\eta \in (0,1)$ (depending on $\delta >0$) and $\epsilon >0$ sufficiently small, this yields a contradiction, if $Q_1 \in \text {O}(2)\setminus {\rm SO}(2)$. Similarly, we also obtain that $Q_2 \in {\rm SO}(2)$. Moreover, since the triangles $\Delta _{cbd}$ with vertices $c, b, d$ and $\Delta _{acd}$ with vertices $a, c, d$ share a common line, we have that $Q_1$ can be chosen equal to $Q_2$ and that $p_1 = p_2$. A normalization further allows us to suppose that $p_1=p_2=0$ and $Q_1 = Q_2 = \operatorname {Id}$. As a consequence, we may assume that

(3.4)\begin{equation} |v(x)-x| \leq C\epsilon^{ 1/2}\quad\text{for }x\in\{a,b,c,d\} \text{ and for some constant }C=C(F,\delta,m). \end{equation}

Step 3: Smallness estimate for $N$: As in [28], we claim that

(3.5)\begin{equation} |N\cap T| \leq C\epsilon^{ 1/2} \text{ for some constant } C=C(F,\delta,m), \end{equation}

where the set $N$ denotes the region where the gradient is closer to the well ${\rm SO}(2)F$ than to the parent gradient, i.e.

(3.6)\begin{equation} N := \left\{x\in B_1: {\rm dist}(\nabla v(x),{\rm SO}(2)F)< {\rm dist}(\nabla v(x),{\rm SO}(2)) \right\}. \end{equation}

To this end, we use the upper length bounds on $v(t)$, i.e. the fact that $v$ is essentially not length increasing. Let $t$ be any point of $[c, d]$. By the fundamental theorem of calculus and lemma 2.3(ii) we then get for some constant $C=C(\delta )>0$

\[ |v(c)-v(t)| \leq |c -t|+\int_{[c,t ]}{\rm dist}(\nabla v,{\rm SO}(2)) \leq |c-t| + C\epsilon^{ 1/2}. \]

Combining this with the triangle inequality and bound (3.4) applied to $x=c$, we obtain

(3.7)\begin{equation} |c-v(t)| \ \mathop{\leq}\limits^{(3.4)}|c-t|+C\epsilon^{ 1/2} \text{ for all $t \in [c, d]$} \end{equation}

and for some constant $C=C(F,\delta, m)>0$. We note that in view of (3.2) and for $\eta = \eta (\delta )$ sufficiently small we can assume that

(3.8)\begin{equation} C\epsilon^{ 1/2} < \ \frac 12 |c-d|. \end{equation}

Next, we seek to use this to deduce lower bounds on $|a- v(t)| + |b - v(t)|$ for $t\in [c,d]$ as above. To this end, we observe that in view of (3.8), the minimization problem

\[ \min\left\{ |a-t'| + |b-t'| \ : \ t' \in B_{r_{c,t}}(c) \text{ with } r_{c,t} := |c- v(t)|\right\} \]

is attained on the line $[c,d]$ and is solved by $t^{\ast }:= t-r ({(c-d)}/{(|c-d|)})$ for some $r$ with $0< r< C\epsilon ^{{1}/{2}}$. Here, the error bound for $r$ is a consequence of (3.7). Using $v(t)$ as a competitor and inserting the bound for $r_{c,t}$ implies

\[ |a- v(t)| + |b - v(t)| \ \geq |a- t^{{\ast}}| + |b - t^*| \geq\ |a - t| + |b - t| - C\epsilon^{ 1/2} \]

for all $t \in [c, d]$. Using again (3.4) now for $x=a$ and $x=b$, we infer the following lower bound on the length deformation for points $t\in [c,d]$:

(3.9)\begin{equation} |v(a) - v(t)| + |v(b) - v(t)| \ \geq\ |a - t| + |b - t| - C\epsilon^{ 1/2}. \end{equation}

We complement this with an upper bound on the length deformation along the segments $[a, t]$ and $[t, b]$, obtained by means of the fundamental theorem. In view of (3.3) and using

\[ |\partial_{\xi}v| \leq 1 + (|F\xi|-1)\chi_N + {\rm dist}(\nabla v, K) \quad \text{for}\ \xi \in \left\{ \frac{a-t}{|a-t|}, \frac{b-t}{|b-t|} \right\} \]

and for any $t\in [c,d]$, where $K := {\rm SO}(2) \cup {\rm SO}(2)F$ and $\chi _N$ denotes the characteristic function of the set $N$ (cf. (3.6)) we get

\[ |v(p) - v(t)| \leq |p - t| +\int_{[p,t ]}{\rm dist}(\nabla v, K) - \delta\int_{[p,t ]}\chi_N\ \quad \text{for}\ p \in \{ a, b \}. \]

Subtracting these estimates from (3.9) we arrive at

\[ \int_{[a,t]\cup[t,b]}\chi_N \leq \delta^{{-}1}\int_{[a,t]\cup[t,b]}{\rm dist}(\nabla v, K) + C\delta^{{-}1}\epsilon^{ 1/2} \quad \text{for any}\ t\in [c,d]. \]

We integrate all $t\in [c, d]$ and change variables from $(x_1,t_2)$ to $(x_1,x_2)$ by the transformation $\Psi (x_1,t_2) = (x_1,t_2 (1- {x_1}/{a_1}))$ (where $t=(0,t_2)$, $a=(a_1,0)$) and $\Phi = \Psi ^{-1}$ to obtain an integration over the rhombus $T$. More precisely, denoting by $J_\Phi (x)$ as the Jacobian determinant of the transformation $\Phi$, we infer

\[ \int_T\chi_N J_\Phi \leq C_{\delta}\int_T{\rm dist}(\nabla v, K) J_\Phi + C\epsilon^{ 1/2}. \]

Since $|J_\Phi | \sim$ ${\rm dist}(x, \{a, b\})^{-1}$, and thus, in particular, $J_\Phi \geq 1$, on the left-hand side we can simply drop $J_\Phi$. For the right-hand side we invoke lemma 2.3(iii) which concludes the argument for (3.5).

Step 4: Conclusion. Last but not least, it remains to estimate $|B_{\alpha }\cap M|$. For $\alpha :={\delta }/{4}$ we have $B_\alpha \subset T$. By definition of $N$ and the triangle inequality we then have

(3.10)\begin{align} \int_{B_\alpha}{{\rm dist}}^2(\nabla v, {\rm SO}(2)) & \leq\ 2{\mathcal{E}}_{\rm elast}[\chi,v,B_\alpha] + 2\int_{B_\alpha \cap N} \|\operatorname{Id}-F\|^2\nonumber\\ & \stackrel{(2.1)}{\leq\ } 2\epsilon+2\|\operatorname{Id}-F\|^2|N\cap T| \mathop{\leq}\limits^{(3.5)} \ C\epsilon^{ 1/2}. \end{align}

By [35, theorem 3.1], we have for some $W,Q\in L^{\infty }(B_{\alpha }, {\rm SO}(2))$,

(3.11)\begin{align} \|{{\rm dist}}& (\nabla v, {\rm SO}(2))\|_{L^2(B_\alpha)} \ \gtrsim\ \left(\int_{B_\alpha}\chi\|\nabla v-W\|^2\right)^{1/2}\nonumber\\ & \geq \left(\int_{B_\alpha}\chi\|QF-W\|^2\right)^{1/2}-\left(\int_{B_\alpha}\chi\|\nabla v-QF\|^2\right)^{1/2}\nonumber\\ & \geq {\rm dist}({\rm SO}(2)F,\operatorname{Id})|M\cap B_\alpha|^{1/2}-\left(\int_{B_\alpha}\chi \text{dist}^2(\nabla v, {\rm SO}(2)F)\right)^{1/2}. \end{align}

Here $Q\in L^{\infty }(B_{\alpha },{\rm SO}(2))$ is such that ${\rm dist}(\nabla v, {\rm SO}(2)F)=\|\nabla v-QF\|$ for almost every $x\in B_{\alpha }$. Hence, we obtain

\begin{align*} |M\cap B_\alpha|& \stackrel{(3.11)}{ \ \leq\ } C \int_{B_\alpha}{\rm dist}^2(\nabla v, {\rm SO}(2))+C\int_{B_\alpha}\chi\text{dist}^2(\nabla v, {\rm SO}(2)F)\\ & \stackrel{(3.10)}{ \leq } C\epsilon^{1/2} \end{align*}

for some constant $C=C(F,\delta, m)>0$. This is the assertion of the theorem.

4. Proof of theorem 1.1

We are ready to give the proof of theorem 1.1. We split it into two parts and first discuss the lower bound and then provide a matching upper-bound construction.

4.1 Proof of the lower bound in theorem 1.1

In this section, we provide the proof of the lower bound. To this end, we first observe that in the small volume regime this directly follows from the isoperimetric inequality. It thus suffices to consider the large volume regime $\mu \geq 1$. Although the proof follows the localization argument as in [42], for the convenience of the reader, we briefly recall its proof.

Proof of theorem 1.1, lower bound. Proof of theorem 1.1, lower bound

Step 1: Strategy. We argue by a localization and covering argument, seeking to invoke proposition 3.1. We consider a suitably chosen countable family of balls $\{B_{R_i}(x_i)\}_{i=1}^\infty$ covering $M:= spt\, \chi$ (see step 2 below). By a Vitali covering argument, we may assume that $\{B_{R_i/5}(x_i)\}_{i=1}^\infty$ are pairwise disjoint. Then, we can localize the energy as follows:

\[ {\mathcal{E}}[\chi, v] \ \geq\ \sum_{i=1}^\infty {\mathcal{E}}_{R_i/5}(x_i), \]

where ${\mathcal {E}}_{R_i}(x_i):= {\mathcal {E}}[\chi, v, B_{R_i}(x_i)]$. Now, if we could bound ${\mathcal {E}}_{R_i/5}(x_i)$ from below in terms of $|M\cap B_{R_i}(x_i)|^{2/3}$ we could conclude the argument

\[ {\mathcal{E}}[\chi, v] \ \geq\ \sum_{i=1}^\infty {\mathcal{E}}_{R_i/5}(x_i) \ \gtrsim\ \sum_{i=1}^\infty |M\cap B_{R_i}(x_i)|^{2/3} \ \gtrsim\ \mu^{2/3}. \]

It thus remains to argue that

\[ {\mathcal{E}}_{R_i/5}(x_i) \ \gtrsim\ |M\cap B_{R_i}(x_i)|^{2/3}. \]

We split this into two steps: following [42], we prove that

(4.1)\begin{align} \displaystyle|M\cap B_{\alpha R_i/5}(x_i)| & \gtrsim\ |M\cap B_{ R_i}(x_i)|; \end{align}

(4.2)\begin{align} \displaystyle{\mathcal{E}}_{R_i/5}(x_i) & \gtrsim\ |M\cap B_{\alpha R_i/5}(x_i)|^{2/3}, \end{align}

where $\alpha >0$ is the constant from proposition 3.1 and for suitably chosen balls $B_{R_i}(x_i)$. We note that all the estimates in this proof may depend on the constant $\alpha$.

Step 2: Choice of radii and centre points $x_i$. To this end, without loss of generality, we may assume that all $x \in M$ are points of density one of $M$. Now for any $x\in M$ we set

(4.3)\begin{equation} R(x):=\inf\left\{r:r^{{-}2}|M\cap B_r(x)| \leq \eta_0\min\{1, |M\cap B_r(x)|^{-(1/3)} \}\right\}, \end{equation}

where $\eta _0$ is sufficiently small constant, which will be fixed later on. By continuity in $r$ and by considering the limit $r\rightarrow \infty$, we infer that $R(x)\leq {\mu ^{2/3}}/{\sqrt {\eta _0}}$. Therefore, $R(x)$ is uniformly bounded in terms of $\mu$ and the defining infimum actually is a minimum. Similarly as in [42], we note that $R=R(x)$ satisfies one of the following conditions: either

(4.4)\begin{equation} |M\cap B_R(x)| \leq\ 1 \text{ and }|M\cap B_R(x)|=\eta_0R^2 \end{equation}

or

(4.5)\begin{equation} |M\cap B_R(x)|> 1 \text{ and }|M\cap B_R(x)|=\eta_0|M\cap B_R(x)|^{-(1/3)}R^2. \end{equation}

Obviously, $M$ is covered by $\cup _{x\in M}B_{R(x)}$. Since the radii $R(x)$ are uniformly bounded, by Vitali's covering lemma, there is an at most countable subset of points $x_i\in \mathbb {R}^2$ such that the balls $\{B_{R_i/5}(x_i)\}_{i=1}^\infty$ are pairwise disjoint while $M$ is still covered by the balls $\{B_{R_i} (x_i)\}_{i=1}^\infty$. This yields the balls and radii from step 1.

Step 3: Proof of estimate (4.1). By the definition of $R$, we obtain the following statements: if $|M\cap B_{R_i} (x_i)|\leq 1$ and $|M\cap B_{\alpha R_i/5}(x_i)|\leq 1$, then

\[ \frac{|M\cap B_{\alpha R_i/5}(x_i)|}{(\alpha R_i/5)^2}\stackrel{(4.3)}{ \ \geq\ }\frac{|M\cap B_{R_i} (x_i)|}{R_i^2} \mathop=\limits^{(4.4)}\eta_0. \]

Analogously, if $|M\cap B_{R_i} (x_i)|> 1$ and $|M\cap B_{\alpha R_i/5}(x_i)|> 1$, then

\[ \frac{|M\cap B_{\alpha R_i/5}(x_i)|^{4/3}}{(\alpha R_i/5)^2}\stackrel{(4.3)}{ \ \geq\ }\frac{|M\cap B_{R_i} (x_i)|^{4/3}}{R_i^2}\mathop=\limits^{(4.5)}\eta_0. \]

Finally, if $|M\cap B_{\alpha R_i/5}(x_i)|\le 1< |M\cap B_{R_i} (x_i)|$, then

\[ \frac{|M\cap B_{\alpha R_i/5}(x_i)|}{(\alpha R_i/5)^2}>\eta_0 \mathop=\limits^{(4.5)}\frac{|M\cap B_{R_i} (x_i)|^{4/3}}{R_i^2}>\frac{|M\cap B_{R_i} (x_i)|}{R_i^2}. \]

The last three obtained estimates together yield bound (4.1).

Step 4: Proof of estimate (4.2). Here, we distinguish three cases: firstly, we assume that case (4.4) holds. Since the density of the minority phase is much smaller than one in $B_{R_i/5}(x_i)$, the use of the isoperimetric inequality implies

\[ \int_{B_{R_i/5}(x_i)}|\nabla \chi| \ \gtrsim\ |M\cap B_{R_i/5}(x_i)|^{ 1/2}\stackrel{(4.1)}{ \ \sim\ }|M\cap B_{R_i} (x_i)|^{ 1/2} \stackrel{(4.4)}{ \ \gtrsim\ }|M\cap B_{R_i} (x_i)|^{2/3}. \]

Secondly, we suppose that case (4.5) and

(4.6)\begin{equation} \int_{B_{R_i/5}(x_i)}|\nabla\chi| \ \gtrsim\ R_i \text{ hold}. \end{equation}

Since $R_i \sim |M\cap B_{R_i} (x_i)|^{2/3}$, we derive

\[ {\mathcal{E}}_{R_i/5}(x_i) \ \gtrsim\ \int_{B_{R_i/5}(x_i)}|\nabla\chi| \stackrel{(4.6)}{ \ \gtrsim\ }|M\cap B_{R_i} (x_i)|^{2/3}. \]

Lastly, we assume that case (4.5) and

\[ \int_{B_{R_i/5}(x_i)} |\nabla\chi| \ \ll\ R_i \text{ hold}, \]

where $\ll$ means that this estimate requires a small universal constant.

Here, choosing $\eta _0$ small enough, the assumptions of proposition 3.1 are fulfilled on $B_{R_i/5}(x_i)$. The use of this proposition results in

\[ {\mathcal{E}}_{R_i/5}(x_i) \ \gtrsim\ \frac{|M\cap B_{\alpha R_i/5}(x_i)|^2}{(\alpha R_i/5)^2}\stackrel{(4.1)}{ \ \sim\ }\frac{|M\cap B_{R_i} (x_i)|^2}{R_i^2} \ \sim\ |M\cap B_{R_i} (x_i)|^{2/3}, \]

as $R_i \sim |M\cap B_{R_i} (x_i)|^{2/3}$. Then, inequality (4.2) follows from the above estimates, which concludes a proof of the lower bound in theorem 1.1.

4.2 Proof of the upper bound of theorem 1.1

We next give the proof of the upper bound in theorem 1.1. For this, we give an explicit construction for an optimal configuration. It suffices to consider the case $\mu \geq 1$, since the case $\mu \leq 1$ follows by simply considering $v(x)=x$ and $\chi = \chi _B$ where $B$ is a ball with $|B| = \mu$. The estimate then follows by using the isoperimetric inequality and noting that $0<\mu \leq \mu ^{{1}/{2}}$ if $\mu \leq 1$. We note that similar constructions are well established (e.g. [40]). An upper bound in the setting of geometrically linear elasticity has also been given in [42] for the geometrically linearized theory. We provide an analogous construction for the geometrically nonlinear case and check that the solutions are within our class of admissible functions. We first note that, by a rotation (see lemma A.1 for more details), we can assume that

\[ F = \operatorname{Id}+\nu\otimes e_2 \text{ for some } \nu = \begin{pmatrix} \nu_1\\0 \end{pmatrix} \in \mathbb{R}^2. \]

In particular $e_2$ is one of the twinning directions for stress-free laminates between $Fx$ and $x$.

As in [42] we consider an inclusion which approximately has the shape of a thin disc $Q_{T,R}$ with diameter $R$ and thickness $T$ where $T \ll R$. The disc is oriented such that the two large surfaces are aligned with the $e_2$ twinning direction. To be more precise, let $x^{(1)},x^{(2)} \in \mathbb {R}^2$ such that $x^{(1)}=-x^{(2)}$ on the axis $x_1=0$ with distance $d := |x^{(1)}-x^{(2)}|$. We define $\chi$ by

\[ \chi\ := \ \chi_{Q_{T,R}}, \quad \text{where } Q_{T,R}:=B_\rho(x^{(1)})\cap B_\rho(x^{(2)}), \]

where $Q_{T,R}$ is the lens with thickness of order $T$ and diameter of order $R$ given by the intersection $B_\rho (x^{(1)})\cap B_\rho (x^{(2)})$ for some suitable $\rho = \rho (R,T)>0$. We choose $T$ such that it fulfils the volume constraint (1.2), i.e. $|Q_{T,R}| = \mu$ and in particular, $RT\sim \mu$.

We next define $u_0 :\mathbb {R}^2 \to \mathbb {R}^2$ such that $u_0(x)= (F - \operatorname {Id}) x$ in $Q_{T,R}$. Furthermore, outside $Q_{T,R}$, $u_0$ is constant on all lines which are normal to the surface $\partial Q_{T,R}$. Finally, $u_0 =0$ in the remaining area which is neither in $Q_{T,R}$ nor reached by any of these lines. The function is sketched in figure 4. Furthermore, let $\omega _R\in C^\infty (\mathbb {R},[0,\infty ])$ be a cut-off function with $\omega _R(\xi )= 1$ for $|\xi | \leq R$ and $\omega _R(\xi ) = 0$ for $|\xi | \ \geq \ 2R$ with $|\nabla \omega _R|\leq {C}/{R}$ for fixed $C>0$. We then define $v :\mathbb {R}^2 \to \mathbb {R}^2$ by

\[ v(x) := (\omega_R u_0)(x)+x. \]

Figure 4. Sketch of the construction of $u_0$ and $v=\omega _R u_0+x$.

Estimates: By construction we have

(4.7)\begin{equation} \|\nabla u_0(x)\| \lesssim\ \begin{cases} 1 & \text{ for }x\in Q_{T,R},\\ TR^{{-}1} & \text{ for } x\notin Q_{T,R} \end{cases} \end{equation}

and $\|u_0\|_{L^\infty ({\mathbb {R}^2})} \lesssim T$. Since $\nabla v = F$ in $Q_{T,R}$ and $\nabla v = \operatorname {Id}$ in $B_{2R}^c$ we get

\begin{align*} {\mathcal{E}}_{\rm elast}[\chi,v] & \leq\ \int_{B_{2R}\backslash Q_{T,R}} {\rm dist}^2(\nabla v,{\rm SO}(2)) \ \lesssim\ \int_{B_{2R}\backslash Q_{T,R}}\|\nabla v-\operatorname{Id}\|_{}^2 \\ & \lesssim\ \int_{B_{2R}\backslash Q_{T,R}} \|\nabla \omega_R\otimes u_0\|_{}^2+\int_{B_{2R}\backslash Q_{T,R}}\|\omega_R \nabla u_0\|_{}^2. \end{align*}

By (4.7), since $RT \sim \mu$ and also including the interfacial part of the energy we obtain

\[ {\mathcal{E}}[\chi, v] \lesssim\ \int_{\mathbb{R}^2} |\nabla \chi| + \int_{B_{2R}\backslash Q_{T,R}} \frac {T^2}{R^2} \ \lesssim\ R + T^2 \lesssim\ R + \frac{\mu^2}{R^2}. \]

The asserted upper bound then follows with the choice $R \sim \mu ^{2/3}$.

Admissibility: We need to check that our construction satisfies $(\chi, v) \in {\mathcal {A}}_m$. In fact, it is enough to check this condition for $\mu = \mu (F)$ and correspondingly $R \sim \mu ^{2/3}$ sufficiently large. We first note that $\chi \in BV(\mathbb {R}^2, \{ 0 , 1\})$ and $\|\nabla v\|_{L^\infty } \leq C \|F\|$. We next consider $v$ locally in the different regions defining it. We show that $v$ is locally invertible and that $\|(\nabla v)^{-1}\|_{L^\infty }{} \leq m$. To this end, we recall that

\[ \nabla v = \nabla \omega_R\otimes u_0 + \omega_R \nabla u_0 + \operatorname{Id}. \]

For $x \not \in B_{2R}$ we have $\nabla v = \operatorname {Id}$. Hence, the restriction of $v$ to the exterior of $B_{2R}$ is invertible on its image and $\|(\nabla v)^{-1}\|_{} =\sqrt {2}\leq \|F\|$. By a similar argument, for $x \in Q_{T,R}$ we have $\nabla v = F$ which implies that $v$ is locally invertible and $\|(\nabla v)^{-1}\|_{} \leq \|F^{-1}\|_{}$. It hence remains to estimate $(\nabla v)^{-1}(x)$ for $x \in B_{2R} \backslash {Q}_{T,R}$. Let $(b_1(x),b_2(x))$ for $x \in B_{2R} \backslash {Q}_{T,R}$ be the mathematical positive-oriented basis where $b_2(x)$ is the direction of the lines in $B_{2R} \backslash {Q}_{T,R}$ where $u_0$ is constant and with sign convention $b_2(x) \cdot e_2 > 0$. By construction we then have $|b_i(x) - e_i| \leq {\mathcal {O}}( T/R)$ for $i = 1,2$. Since $\nabla u_0(x) b_2(x) = 0$ we hence get $|\nabla u_0 e_2| \leq {(C \|F\| T)}/{R}$. Since $(F-\operatorname {Id})e_1 = 0$ we also have $|\nabla u_0(x) b_1(x)| \leq {(C \|F\| T)}/{R}$. Together, this yields $\|\nabla u_0\|_{} \leq {(C \|F\| T)}/{R}$. Since $|\omega _R| \leq 1$ and $|\nabla \omega _R| \lesssim 1/R$, this yields

\[ \|\nabla \omega_R\otimes u_0 + \omega_R \nabla u_0\| \leq\ \frac {C \|F\| (1+T)}{R}. \]

In particular,

\[ \|\nabla v - \operatorname{Id}\|_{} \leq \frac {C \|F\| (1+T)}{R}\leq C \|F\|\mu^{-(1/3)} \]

as $R\sim \mu ^{2/3}$, $T\sim \mu ^{1/3}$ and $\mu \geq 1$. As a consequence, a Neumann series argument then implies that the restriction of $v$ to $B_{2R} \setminus Q_{T,R}$ is invertible on its image and

\[ \|(\nabla v)^{{-}1}(x)\|\leq C(1+\|\nabla v(x)- \operatorname{Id}\|) \leq C\|F\| \]

for $R = R(\|F\|)$ sufficiently large.

Last but not least, we argue that with the observations for $\nabla v$ from above, we obtain that $v$ is globally invertible. To this end, it suffices to prove that $v$ is injective. Assuming that for some $x,y\in \mathbb {R}^2$ we have that $v(x)=v(y)$, the fundamental theorem yields that

\[ 0 = \left( \int\nolimits_{0}^1 \nabla v(tx+(1-t)y)\,{\rm d}t \right) (x-y). \]

Since the arguments from above show that $\nabla v$ always is a perturbation of an upper triangular matrix, this can only be the case if $x=y$ which hence implies the desired injectivity.