Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T10:41:58.729Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiplicity and bifurcation of periodic solutions in ordinary differential equations

Published online by Cambridge University Press:  14 November 2011

B. Laloux
B. Laloux
Affiliation:
Université Catholique de Louvain, Louvain-la-Neuve, Belgium
Get access Rights & Permissions [Opens in a new window]

Synopsis

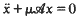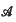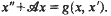One considers the linear differential systems where is a (not necessarily diagonal) matrix and one relates the computation of a general multiplicity defined from this system to the corresponding multiplicity of some eigenvalues of . Then applying these conclusions, one gives simple conditions ensuring the existence of odd or even periodic solutions for systems having the form .

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 82 , Issue 3-4 , 1979 , pp. 225 - 232
Copyright
Copyright © Royal Society of Edinburgh 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Bonic., R. A.Linear Functional Analysis (New York: Gordon and Breach, 1969).Google Scholar
2Berger, M. S.. On periodic solutions of second order Hamiltonian systems, I. J. Math. Anal. Appl. 29 (1970), 512–522.CrossRefGoogle Scholar
3Gaines, R. and Mawhin, J.. Coincidence Degree and Nonlinear Differential Equations (Berlin: Springer, 1977).CrossRefGoogle Scholar
4Laloux., B. Indice de coincidence et bifurcations. In Equations Différentielles et fonctionnelles non linéaires, eds P., Janssens, J., Mawhin and N., Rouche, pp. 109–121. (Paris: Hermann, 1973).Google Scholar
5Laloux, B.Periodic solutions of some autonomous ordinary differential equations. Ann. Soc. Sci. Bruxelles 91 (1977), 62–68.Google Scholar
6Laloux, B. andMawhin, J.. Multiplicity, Leray-Schauder formula and bifurcation. J. Differential Equations 24 (1977), 309–322.CrossRefGoogle Scholar
7Lazer, A. C.. Topological degree and symmetric families of periodic solutions of non-dissipative second-order systems. J. Differential Equations 19 (1975), 62–69.CrossRefGoogle Scholar
8Pliss, V. A.. Families of periodic solutions of dissipationless systems of second order differential equations. Differential'nye Uravneniya 1 (1965), 1428–1448.Google Scholar