Non-existence of radial backward self-similar blow-up solutions with sign change

Abstract

We consider a Cauchy problem for a semilinear heat equation

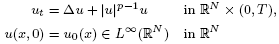
with p > 1. If u(x, t) = (T − t)^−1/(p−1)ϕ((T − t)^−1/2x) for x ∈ ℝ^N and t ∈ [0, T),

where ϕ ∈ L^∞(ℝ^N) is a solution not identically equal to zero of

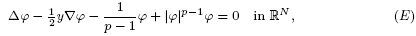
then u is called a backward self-similar solution blowing up at t = T. We show that, for all p > 1, there exists no radial sign-changing solution of (E) which belongs to L^∞(ℝ^N). This implies the non-existence of radial backward self-similar solution with sign change blowing up in finite time.