Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ortega, Rafael
1992.
Critical growth for a superlinear elliptic problem in two dimensions.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 19,
Issue. 8,
p.
731.
Amster, P.
De Nápoli, P.
and
Mariani, M.C.
2005.
An -dimensional pendulum-like equation via topological methods.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 60,
Issue. 2,
p.
389.
Amster, P.
and
Mariani, M.C.
2006.
A system of coupled pendulii.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 64,
Issue. 8,
p.
1647.
Amster, Pablo
and
Maurette, Manuel
2012.
An elliptic singular system with nonlocal boundary conditions.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 75,
Issue. 15,
p.
5815.
Bartolucci, Daniele
and
Jevnikar, Aleks
2022.
On the uniqueness and monotonicity of solutions of free boundary problems.
Journal of Differential Equations,
Vol. 306,
Issue. ,
p.
152.


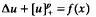 in Ω. The existence of a solution was previously established assuming that
in Ω. The existence of a solution was previously established assuming that 