Article contents
A nonlinear pseudoparabolic equation
Published online by Cambridge University Press: 14 November 2011
Synopsis
The authors prove results on uniqueness and global existence of initial and boundary value problems for the nonlinear pseudoparabolic equation
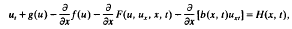
with nonhomogeneous boundary conditions. A salient feature of the paper is that F and its partial derivatives are allowed to be unbounded. In the special case b(x, t)= α2 (a positive constant), it is proved that the corresponding solution uα, under appropriate conditions on the data (which are satisfied, for example, by the Benjamin–Bona–Mahony equation), uα→ u0 the solution corresponding to β = 0, on sufficiently small time interval. A result on the asymptotic behaviour of the solution is given for t → ∞.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 114 , Issue 1-2 , 1990 , pp. 119 - 133
- Copyright
- Copyright © Royal Society of Edinburgh 1990
References
- 3
- Cited by


