On a partial theta function and its spectrum

Extract

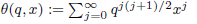The bivariate series defines a partial theta function. For fixed q (∣q∣ < 1), θ(q, ·) is an entire function. For q ∈ (–1, 0) the function θ(q, ·) has infinitely many negative and infinitely many positive real zeros. There exists a sequence 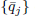of values of q tending to –1⁺ such that 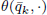has a double real zero 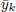(the rest of its real zeros being simple). For k odd (respectively, k even) 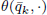has a local minimum (respectively, maximum) at 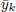, and 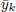is the rightmost of the real negative zeros of 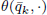(respectively, for k sufficiently large 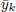is the second from the left of the real negative zeros of 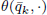). For k sufficiently large one has 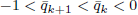. One has 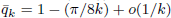and 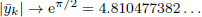.