On a quasilinear elliptic problem involving the 1-Laplacian operator and a discontinuous nonlinearity

Abstract

In this work, we study a quasilinear elliptic problem involving the 1-Laplacian operator, with a discontinuous, superlinear and subcritical nonlinearity involving the Heaviside function $H(\cdot - \beta )$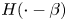. Our approach is based on an analysis of the associated p-Laplacian problem, followed by a thorough analysis of the asymptotic behaviour or such solutions as $p \to 1^+$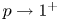. We study also the asymptotic behaviour of the solutions, as $\beta \to 0^+$ 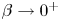and we prove that it converges to a solution of the original problem, without the discontinuity in the nonlinearity.

1. Introduction

In this work we study the following quasilinear elliptic equation

(1.1)\begin{equation} \begin{cases} \displaystyle -\Delta_1 u = H(u - \beta)|u|^{q-2}u & \mbox{in} \quad \Omega \\ \qquad u =0 & \mbox{on} \quad \partial\Omega, \end{cases} \end{equation}

where the 1-Laplacian operator is formally defined as $\Delta _1 u = \mbox {div}(Du/|Du|)$, $\Omega \subset \mathbb {R}^N$ is a bounded domain with a Lipschitz boundary, $N \geq 2$, $1 < q < N/(N-1),$ $\beta >0$ is a real parameter and $H: \mathbb {R}\rightarrow \mathbb {R}$ is the Heaviside function $H(t) = 1$ if $t \geq 0$ and $H(t) = 0$ otherwise.

In recent decades, the study of nonlinear partial differential equations with discontinuous nonlinearities has attracted the attention of several researchers. One of the reasons to study such equations is due to many free boundary problems arising in mathematical physics which can be stated in this form. Among these problems, we have the obstacle problem, the seepage surface problem, and the Elenbaas equation, see [15–17]. For more applications see [4]. Several techniques have been developed or applied to study this kind of problem, such as variational methods for nondifferentiable functionals, lower and upper solutions, dual variational principle, global branching, Palais principle of symmetric criticality for locally Lipschitz functional and the theory of multivalued mappings. See for instance, Alves, Yuan and Huang [1], Alves, Santos and Nemer [2], Ambrosetti and Badiale [3], Ambrosetti, Calahorrano and Dobarro [4], Ambrosetti and Turner [5], Anmin and Chang [11], Arcoya and Calahorrano [13], Cerami [14], Chang [15–17], Clarke [20, 21], Gazzola and Rădulescu [24], Krawcewicz and Marzantowicz [28], Molica Bisci and Repovš [30], Rădulescu [34], dos Santos and Figueiredo [23] and their references.

As far as problems involving the 1-Laplacian operator are concerned, there are at least two approaches one can follow. The first one is based on the study of the energy functional associated to the problem, which is defined in $BV(\Omega )$, whenever one can write it as the difference of a convex and locally Lipschitz functional and a $C^1$ one. Then, one can use the tools of nonsmooth nonlinear analysis (see [17, 21, 33]) to find critical points of such energy functional. Note that, in studying (1.1), this is far from being an option for us, since the energy functional associated to (1.1) would be defined in $BV(\Omega )$, and given by

\[ I_H(u) = \|u\|_{BV(\Omega)} - \mathcal{F}_\beta(u), \]

where $\mathcal {F}_\beta (u)\,{=}\,\int _{\Omega } F_H(u)\,{\rm d}x$, with $f_H(s)\,{=}\,H(s\,{-}\,\beta )|s|^{q-2}s$ and $F_H(t) \,{=}\, \int _0^t f_H(s)\,{\rm d}x$. Hence, since $\mathcal {F}_\beta$ is not a $C^1$ functional defined on $BV(\Omega )$, it would be tricky to show that a critical point of $I_H$ satisfies (1.1) in some sense, since in this case, we could not use variational inequalities to follow the standard approach, which is based on that one proposed by [33].

Fortunately, there is another approach which is based on the study of (1.1), with the 1-Laplacian substituted by the p-Laplacian operator, for $p > 1$. Then, one can use standard arguments to solve the associated problem and then studying the family of such solutions as $p \to 1^+$. To the best of our knowledge, the pioneering works involving this operator were written by F. Andreu, C. Ballesteler, V. Caselles and J.M. Mazón in a series of papers (among them [7–9]), which gave rise to the monograph [10]. Among the very first works on this issue we should also cite the works of Kawohl [27] and Demengel [22].

Before to state our main result, let us define what we mean by a solution of the problem (1.1). Inspired by locally Lipschitz continuous functionals [17, 20, 21, 26] and Anzellotti–Frid–Chen's Pairing Theory [12, 19] (see subsections 2.2 and 2.1 for more details), we say that $u \in BV(\Omega )$ is a bounded variation solution of (1.1), if there exist $\rho \in L^{\frac {q}{q-1}}(\Omega )$ and ${\textbf z} \in X_N(\Omega )$ with $\|{\textbf z}\|_\infty \leq 1$, such that

(1.2)\begin{equation} \left\{ \begin{array}{@{}rcl} - \mbox{div}\, {\textbf z} & = & \rho \quad \mbox{ in }\mathcal{D}'(\Omega),\\ ({\textbf z},Du) & = & |Du| \quad \mbox{in }\mathcal{M}(\Omega),\\ {[{\textbf z},\nu]} & \in & sign({-}u) \quad \mathcal{H}^{N-1}\mbox{-a.e. on}\ \partial \Omega, \end{array}\right. \end{equation}

and it holds that, for almost every $x\in \Omega,$

(1.3)\begin{equation} \rho(x) \in \begin{cases} \{0\}, & \ \mbox{if} \ u(x)<\beta,\\ [0, \beta^{q-1}], & \ \mbox{if} \ u(x)=\beta\\ \{u(x)^{q-1}\}, & \ \mbox{if} \ u(x)>\beta. \end{cases}\end{equation}

It is important to point out here that if the set $\{x\in \Omega : u(x)=\beta \}$ has zero Lebesgue measure, then $\rho (x)=H(u(x)-\beta )|u(x)|^{q-2}u(x)$ for almost every $x\in \Omega$.

Motivated by the works previously mentioned, our first main result is the following.

Theorem 1.1 Suppose that $N \geq 2$ and $1 < q < N/(N-1)$. Then, for each $\beta > 0,$ (1.1) admits at least one nonnegative and nontrivial solution $u_\beta \in BV(\Omega )\cap L^{\infty }(\Omega ),$ in the sense of (1.2).

In the scope of the last theorem, a question which naturally arises is about the behaviour of the solutions $u_\beta$, as $\beta \to 0^+$. In fact, one should expect that $u_\beta$ converges in some sense, as $\beta \to 0^+$, to a solution of the following problem

(1.4)\begin{equation} \begin{cases} \displaystyle -\Delta_1 u = |u|^{q-2}u & \mbox{in} \quad \Omega \\ \qquad u =0 & \mbox{on} \quad \partial\Omega. \end{cases} \end{equation}

In the next theorem, we prove that this in fact occurs.

Theorem 1.2 For each $\beta > 0,$ let $u_\beta$ be the solution given in theorem 1.1. Then there exists a nontrivial and nonnegative solution of (1.4) , $u_0 \in BV(\Omega ),$ such that, as $\beta \to 0^+,$

\[ u_\beta \to u_0 \quad \mbox{in}\ L^r(\Omega),\ \mbox{for all}\ 1 \leq r < N/(N-1)\ \mbox{and also a.e. in}\ \Omega. \]

Moreover, there exist positive constants $\mu$ and $\beta _{0},$ such that

(1.5)\begin{equation} |\{x\in \Omega: u_\beta(x)>\beta\}|\geq \mu, \ \mbox{ for all } \ \beta\in(0, \beta_{0}), \end{equation}

where $|A|$ denotes the measure of a measurable set $A\subset \mathbb {R}^N$.

Note that the last part of the theorem guarantees that the set $\{u_\beta > \beta \}$ does not shrink as $\beta \to 0$, that is, $\|u_\beta \|_{L^\infty (\Omega )}> \beta$, for $\beta$ small enough. Such an information is quite relevante because it ensures that, at least for $\beta$ small, $u_{\beta }$ is in fact a solution of a problem involving a discontinuous nonlinearity.

The existence of positive solution for (1.1) with $\beta =0$ (i.e., (1.4)) was recently studied by Molino-Segura in [32]. Due to the discontinuity in (1.1), caused by the Heaviside function (with $\beta >0$), we cannot use the classical critical point theory for $C^1$ functionals as in [32]. For this reason, motivated by [5, 13, 17, 18, 20, 21], we combine variational methods for nondifferentiable functionals with the approximation argument of [32].

In theorem 1.1, to prove the boundedness of the solutions, we use Moser's iteration method (see [31]) and a careful analysis of some constants to obtain a uniform estimate in the $L^\infty (\Omega )-$norm of the solutions of the approximate problem. These estimates were essential in our arguments to ensure that the solution of problem (1.1) is nontrivial.

This paper is organized as follows. In § 2 we present some definitions and basic results about functions of bounded variation and the nonlinear analysis involving nonsmooth functionals. In § 3 and 4, we present the proofs of theorem 1.1 and 1.2, respectively.

2. Preliminaries

2.1 Main properties of $BV(\Omega )$ space

First of all let us introduce the space of functions of bounded variation, $BV(\Omega )$, where $\Omega \subset \mathbb {R}^N$ is a domain. We say that $u \in BV(\Omega )$, or is a function of bounded variation, if $u \in L^1(\Omega )$, and its distributional derivative $Du$ is a vectorial Radon measure, i.e.,

\[ BV(\Omega) = \left\{u \in L^1(\Omega); \, Du \in \mathcal{M}(\Omega,\mathbb{R}^N)\right\}. \]

It can be proved that $u \in BV(\Omega )$ if and only if $u \in L^1(\Omega )$ and

\[ \int_{\Omega} |Du| := \sup\left\{\int_{\Omega} u \, \mbox{div}\, \phi \,{\rm d}x; \, \, \phi \in C^1_c(\Omega,\mathbb{R}^N), \, \|\phi\|_\infty \leq 1\right\} <{+}\infty. \]

The space $BV(\Omega )$ is a Banach space when endowed with the norm

\[ \|u\|_{BV} := \int_{\Omega} |Du| + \int_{\Omega}|u|\,{\rm d}x, \]

which is continuously embedded into $L^r(\Omega )$ for all $\displaystyle r \in [1,\,1^*]$, where ${1^* = N/(N-1)}$. Since the domain $\Omega$ is bounded, it holds also the compactness of the embeddings of $BV(\Omega )$ into $L^r(\Omega )$ for all $\displaystyle r \in [1,\,1^*)$.

The space $C^\infty (\overline {\Omega })$ is not dense in $BV(\Omega )$ with respect to the strong convergence. However, with respect to the strict convergence, it does. We say that $(u_n) \subset BV(\Omega )$ converges to $u \in BV(\Omega )$ in the sense of the strict convergence, if

\[ u_n \to u, \quad \mbox{in}\ L^1(\Omega) \]

and

\[ \int_{\Omega}|Du_n| \to \int_{\Omega}|Du|, \]

as $n \to \infty$. In [6] one can see also that it is well defined a trace operator $BV(\Omega ) \hookrightarrow L^1(\partial \Omega )$, in such a way that

\[ \|u\| := \int_{\Omega} |Du| + \int_{\partial\Omega}|u|d\mathcal{H}^{N-1}, \]

is a norm equivalent to $\|\cdot \|_{BV}$.

Given $u \in BV(\Omega )$, we can decompose its distributional derivative as

\[ Du = D^au + D^su, \]

where $D^au$ is absolutely continuous with respect to the Lebesgue measure $\mathcal {L}^N$, while $D^su$ is singular with respect to the same measure. Moreover, we denote the total variation of $Du$, as $|Du|$.

In several arguments we use in this work, it is mandatory to have a sort of Green's Formula to expressions like $w \, \mbox {div}({\textbf z})$, where ${\textbf z} \in L^\infty (\Omega,\,\mathbb {R}^N)$, $\mbox {div}({\textbf z}) \in L^N(\Omega )$ and $w \in BV(\Omega )$. For this we have to somehow deal with the product between ${\textbf z}$ and $Dw$, which we denote by $({\textbf z},\,Dw)$. This can be done through the pairings theory, developed by Anzellotti in [12] and independently by Frid and Chen in [19]. Below, we describe the main results of this theory.

Let us denote

\[ X_N(\Omega) = \left \{{\textbf z} \in L^\infty(\Omega,\mathbb{R}^N); \, \mbox{div}({\textbf z}) \in L^N(\Omega) \right \}. \]

For ${\textbf z} \in X_N(\Omega )$ and $w \in BV(\Omega )$, we define the distribution $({\textbf z},\,Dw) \in \mathcal {D}'(\Omega )$ as

\[ \langle ({\textbf z},Dw), \varphi \rangle :={-} \int_\Omega w \varphi \, \mbox{div}({\textbf z})\,{\rm d}x - \int_\Omega w {\textbf z}\cdot \nabla \varphi \,{\rm d}x, \]

for every $\varphi \in \mathcal {D}(\Omega )$. With this definition, it can be proved that $({\textbf z},\,Dw)$ is in fact a Radon measure such that

(2.1)\begin{equation} \left|\int_B ({\textbf z},Dw)\right| \leq \|{\textbf z}\|_\infty \int_B |Dw|,\end{equation}

for every Borel set $B \subset \Omega$.

In order to define an analogue of the Green's Formula, it is also necessary to describe a weak trace theory for ${\textbf z}$. In fact, there exists a trace operator $[ \cdot,\, \nu ]: X_N(\Omega ) \to L^\infty (\partial \Omega )$ such that

(2.2)\begin{equation} \|\left[{\textbf z}, \nu\right]\|_{L^\infty(\partial \Omega)} \leq \|{\textbf z}\|_\infty\end{equation}

and, if ${\textbf z} \in C^1(\overline {\Omega }_\delta,\,\mathbb {R}^N)$,

\[ \left[{\textbf z}, \nu\right](x) = {\textbf z}(x)\cdot \nu(x) \quad \mbox{on }\Omega_\delta, \]

where by $\Omega _\delta$ we denote a $\delta$-neighbourhood of $\partial \Omega$. With these definitions, it can be proved that the following Green's Formula holds for every ${\textbf z} \in X_N(\Omega )$ and $w \in BV(\Omega )$,

(2.3)\begin{equation} \int_\Omega w\, \mbox{div}({\textbf z})\,{\rm d}x + \int_\Omega ({\textbf z},Dw) = \int_{\partial \Omega}[{\textbf z},\nu] w d\mathcal{H}^{N-1}.\end{equation}

2.2 Nonlinear analysis on nondifferentiable functionals

In this subsection, for the reader's convenience, we recall some definitions and basic results on the critical point theory of locally Lipschitz continuous functionals (that is based on the subdifferential theory of Clarke [20, 21]) as developed by Chang [17], Clarke [20, 21] and Grossinho and Tersian [26].

Let $E$ be a real Banach space. A functional $I:E \rightarrow {\mathbb {R}}$ is locally Lipschitz continuous, $I \in Lip_{loc}(E,\, {\mathbb {R}})$ for short, if given $u \in E$ there is an open neighbourhood $V := V_u \subset E$ and some constant $M = M_V > 0$ such that

\[{\mid} I(v_2) - I(v_1) \mid\leq M \| v_2-v_1 \|, \quad v_i\in V, \ i = 1,2. \]

The directional derivative of $I$ at $u$ in the direction of $v \in E$ is defined by

\[ I^0(u;v)=\displaystyle \displaystyle \limsup_{h \to 0,~\sigma \downarrow 0} \frac{I(u+h+ \sigma v)-I(u+h)}{\sigma}. \]

Hence $I^0(u;.)$ is continuous, convex and its subdifferential at $z\in E$ is given by

\[ \partial I^0(u;z):=\big\{\mu\in E^*;I^0(u;v)\geq I^0(u;z)+ \langle\mu,v-z\rangle, \ v\in E\big\}, \]

where $\langle.,\,.\rangle$ is the duality pairing between $E^*$ and $E$. The generalized gradient of $I$ at $u$ is the set

\[ \partial I(u):=\big\{\mu\in E^*; \langle \mu,v\rangle\leq I^0(u;v), \ v\in E\big \}. \]

Since $I^0(u;0) = 0$, $\partial I(u)$ is the subdifferential of $I^0(u;.)$ in $0$.

It is also known that $\partial I(u)\subset E^*$ is convex, nonempty and weak*-compact and it is well defined

(2.4)\begin{equation} \Lambda_I (u): = \min \big\{\!\!\parallel\mu\parallel_{E^*};\mu \in \partial I(u) \big \}. \end{equation}

A critical point of $I$ is an element $u_\beta \in E$ such that $0\in \partial I(u_\beta )$ and a critical value of $I$ is a real number $c$ such that $I(u_\beta )=c$ for some critical point $u_\beta \in E$.

We say that $I\in Lip_{loc}(E,\, \mathbb {R})$ satisfies the nonsmooth Palais–Smale condition at level $c\in \mathbb {R}$ (nonsmooth $(PS)_c$-condition for short), if the following holds: every sequence $(u_n)\subset E$, such that $I(u_n)\rightarrow c$ and $\Lambda _I(u_n)\rightarrow 0$ has a strongly convergent subsequence.

Proposition 2.1 See [20, 21, 26]

Let $I_1,\, I_2: E\rightarrow \mathbb {R}$ be locally Lipschitz functions, then:

1. (i) $I_1+ I_2\in Lip_{loc}(E,\,\mathbb {R})$ and $\partial (I_1+ I_2)(u) \subseteq \partial I_1(u) + \partial I_2(u),$ for all $u\in E.$

2. (ii) $\partial (\lambda I_1)(u) = \lambda \partial I_1(u)$ for each $\lambda \in \mathbb {R},\, u\in E.$

3. (iii) Suppose that for each point $v$ in a neighbourhood of $u,$ $I_1$ admits a Gateaux derivative $I_1'(v)$ and that $I_1' :E\rightarrow E^*$ is continuous, then $\partial I_1(u) = \{I_1'(u)\}.$

Theorem 2.2 See [20, 21, 26]

Let $E$ be a Banach space and let $I\in Lip_{loc}(E,\,\mathbb {R})$ with $I(0) = 0.$ Suppose there are numbers $\alpha,\,r>0$ and $e\in E,$ such that

1. (i) $I(u)\geq \alpha,$ for all $u\in E; \|u\|=r,$

2. (ii) $I(e)<0$ and $\|e\|>r.$

Let

(2.5)\begin{equation} c=\inf_{\gamma\in\Gamma}\max_{t\in[0,1]} I(\gamma(t)) \mbox{ and } \Gamma=\{\gamma\in C([0,1],E): \gamma(0)=0\ \mbox{ and } \gamma(1)=e\}. \end{equation}

Then $c\geq \alpha$ and there is a sequence $(u_{n})\subset E$ satisfying

\[ I(u_{n})\rightarrow c\ \mbox{ and } \ \Lambda_{I}(u_{n})\rightarrow0. \]

If, in addition, $I$ satisfies the nonsmooth $(PS)_c$-condition, then $c$ is a critical value of $I.$

3. Proof of theorem 1.1

In this section, to prove our main result, we will consider a family of auxiliary problems involving the p-Laplacian operator and discontinuous nonlinearity. We will use an approximation technique and variational methods for nondifferentiable functionals inspired by Molino-Segura de León [32], Anzellotti-Frid-Chen [12, 19], Arcoya-Calahorrano [13], Ambrosetti-Turner [5], Clarke [20] and Chang [17].

In order to get such solutions of (1.1), the first step is to consider the problem

(3.1)\begin{equation} \begin{cases} \displaystyle -\mbox{div}\left(|\nabla u|^{p-2}\nabla u\right) = H(u - \beta)|u|^{q-2}{u} & \mbox{in} \quad \Omega, \\ \qquad u =0 & \mbox{on} \quad \partial\Omega. \end{cases} \end{equation}

We say that $u_{p,\beta } \in W^{1,p}_0(\Omega )$ is a weak solution of (3.1), if there exists $\rho _{p,\beta } \in L^{\frac {q}{q-1}}(\Omega )$, such that

(3.2)\begin{equation} \int_\Omega |\nabla u_{p,\beta}|^{p-2}\nabla u_{p,\beta} \nabla \varphi \,{\rm d}x = \int_\Omega \rho_{p,\beta} \varphi \,{\rm d}x, \ \mbox{ for all } \ \varphi \in W^{1,p}_0(\Omega), \end{equation}

and it holds that, for almost every $x\in \Omega,$

(3.3)\begin{equation} \rho_{p,\beta}(x) \in \begin{cases} \{0\}, & \ \mbox{if} \ u_{p,\beta}(x)<\beta,\\ [0, \beta^{q-1}], & \ \mbox{if} \ u_{p,\beta}(x)=\beta, \\ \{u_{p,\beta}(x)^{q-1}\}, & \ \mbox{if} \ u_{p,\beta}(x)>\beta. \end{cases}\end{equation}

Inspired by Arcoya and Calahorrano [13], which proved the existence of solution for a sublinear version of (3.1) (see also Ambrosetti and Turner [5]), we will use the nonsmooth critical point theory to prove that problem (3.1) has at least one solution $u_{p,\beta }\in W_0^{1,p}(\Omega )$, which will be obtained by the nonsmooth version of the Mountain pass theorem (see theorem 2.2). Furthermore, we will prove some properties of this solution that will be useful to prove the existence of a solution to problem (1.1). To achieve this goal, first note that by Chang's results [17, theorem 2.1 and theorem 2.3], the functional $\mathcal {F}_\beta : L^q(\Omega )\rightarrow \mathbb {R}$ given by

\[ \mathcal{F}_\beta(u)=\int_{\Omega} F_\beta(u)\,{\rm d}x, \mbox{ with}\ f_\beta(s) = H(s-\beta)|s|^{q-2}s\ \mbox{and}\ F_\beta(t) = \int_0^t f_\beta(s)\,{\rm d}x, \]

is locally Lipschitz and

(3.4)\begin{equation} \partial \mathcal{F}_\beta(u)=[\underline{f}_\beta(u),\overline{f}_\beta(u)] \ \mbox{ a.e. in } \Omega, \end{equation}

where

\begin{align*} \underline{f}_\beta(t)& = \lim_{r\rightarrow0^+} \mbox{ess inf}\{f_\beta(s): |t-s| < r\} \ \mbox{ and }\\ \overline{f}_\beta(t) & = \lim_{r\rightarrow0^+} \mbox{ess sup}\{f_\beta(s): |t-s| < r\}. \end{align*}

It is clear that

(3.5)\begin{equation} [\underline{f}_\beta(t),\overline{f}_\beta(t)]=\begin{cases} \{0\}, & \ \mbox{if} \ t<\beta,\\ [0, \beta^{q-1}], & \ \mbox{if} \ t=\beta,\\ \{t^{q-1}\}, & \ \mbox{if} \ t>\beta. \end{cases}\end{equation}

The associated functional for (3.1) is $J_{p,\beta }: W_{0}^{1,p}(\Omega )\rightarrow \mathbb {R}$, given by

(3.6)\begin{equation} J_{p,\beta}(u)=Q_p(u)- \mathcal{F}_\beta\bigl|_{W_0^{1,p}}(u), \ \mbox{where} \ Q_p(u)=\frac{1}{p}\int_{\Omega}|\nabla u|^p\,{\rm d}x. \end{equation}

Due to the presence of the Heaviside function $H,$ the functional $J_{p,\beta }$ is not Fréchet differentiable, but is locally Lipschitz on $W_0^{1,p}(\Omega )$. Moreover, by [17, theorem 2.2] we have $\partial (\mathcal {F}_{H}\bigl |_{W_0^{1,p}})(u)=\partial \mathcal {F}_\beta (u),$ for all $u\in W_0^{1,p}(\Omega ).$ Hence, by proposition 2.1,

(3.7)\begin{equation} \partial J_{p,\beta}(u)=\{Q_p'(u)\}-\partial \mathcal{F}_\beta(u) \ \mbox{ for all } u\in W_0^{1,p}(\Omega), \end{equation}

and therefore, by (3.4), (3.5) and (3.7), critical points of $J_{p,\beta },$ in the sense of the nonsmooth critical point theory, will give rise to solutions of (3.1).

Since we want to find a nontrivial solution of (1.1) by using the solutions $u_{p,\beta }$ of (3.1) by passing to the limit as $p\rightarrow 1^+,$ in what follows, we will consider $p\in (1,\,\overline {p})$ for some $\overline {p}\in (1,\,q)$ fixed.

Lemma 3.1 For each $p\in (1,\,\overline {p})$ and $\beta >0,$ the functional $J_{p,\beta }$ satisfies the geometric conditions of the Mountain pass theorem. More precisely,

1. (i) There exist $r,\,\alpha >0,$ which are independent of $\beta,$ such that $J_{p,\beta }(u)\geq \alpha$ for all $u\in W_0^{1,p}(\Omega )$ with $\|u\|_{W_0^{1,p}(\Omega )}=r.$ Moreover, $\alpha$ can be chosen also independent of $p$.

2. (ii) There exists $e = e(\beta )\in C_0^{\infty }(\Omega )$ such that $J_{p,\beta }(e) < 0$ and $\|e\|_{W_0^{1,p}(\Omega )}> r.$

Proof. By Hölder's inequality,

\[ J_{p,\beta}(u) \geq \frac{1}{p}\|\nabla u\|_{L^p(\Omega)}^p - \biggl(\int_{\Omega}|u|^{p^*}\biggl)^{\frac{q}{p^*}}|\Omega|^{\frac{p^*-q}{p^*}}, \mbox{ for all } u\in W_0^{1,p}(\Omega). \]

Since, by [25, proof of theorem 7.10], for each $u\in W_0^{1,p}(\Omega ),$

(3.8)\begin{equation} \|u\|_{L^{p^*}(\Omega)}\leq \frac{\theta}{\sqrt{N}}\|\nabla u\|_{L^{p}(\Omega)}, \mbox{ where } \theta=\frac{p(N-1)}{N-p}, \end{equation}

we have,

\begin{align*} J_{p,\beta}(u) & \geq\frac{1}{p}\|\nabla u\|_{L^{p}(\Omega)}^p - |\Omega|^{\frac{p^*-q}{p^*}}\biggl(\frac{p(N-1)}{\sqrt{N}(N-p)}\biggl)^{q} \|\nabla u\|_{L^{p}(\Omega)}^q\\ & \geq \frac{1}{\overline{p}}\|\nabla u\|_{L^{p}(\Omega)}^p - C\|\nabla u\|_{L^{p}(\Omega)}^q, \mbox{ for all } u\in W_0^{1,p}(\Omega), \end{align*}

where $C=\bigl (\overline {p}(N-1)/\sqrt {N}(N-\overline {p})\bigl )^{q}\max \{1,\,|\Omega |\}.$

Note that

\begin{align*} \frac{r^p}{\overline{p}} - Cr^{q}\geq \frac{r^q}{\overline{p}} \ \text{ if and only if } 0< r\leq\biggl(\frac{1}{\overline{p}C+1}\biggl)^{\frac{1}{q-p}}.\end{align*}

Then, by choosing $r=\biggl (\frac {1}{\overline {p}C+1}\biggl )^{\frac {1}{q-\overline {p}}}$ and $\alpha =r^{q}/\overline {p},$ we conclude that $(i)$ holds.

Now, let $\varphi \in C^{\infty }_0(\Omega )$ be such that $|\{\varphi >\beta \}|>0,$ where $\{\varphi >\beta \}$ denotes the set $\{x\in \Omega : \varphi (x) > \beta \}.$ For each $t\geq 1,$ we get

\begin{align*} J_{p,\beta}(t\varphi) & = \frac{t^p}{p}\| \varphi \|_{W_0^{1,p}(\Omega)}^p- \int_{\Omega}F_\beta(t\varphi)\,{\rm d}x \\ & \leq \frac{t^p}{p}\| \varphi \|_{W_0^{1,p}(\Omega)}^p-\frac{t^q}{q}\int_{\{\varphi>\beta\}}\varphi^q \,{\rm d}x +\frac{\beta^{q}}{q}|\Omega|, \end{align*}

which implies in the existence of $e$ satisfying $(ii).$

Lemma 3.2 For each $p\in (1,\,\overline {p})$ and $\beta >0,$ $J_{p,\beta }$ satisfies the nonsmooth Palais–Smale condition.

Proof. Let $(u_n)\subset W_0^{1,p}(\Omega )$ be a $(PS)_c$ sequence for $J_{p,\beta },$ that is, $J_{p,\beta }(u_n) \to c$ and $\Lambda _{J_{p,\beta }}(u_{n})\rightarrow 0,$ where $\Lambda _{J_{p,\beta }}$ is defined in (2.4). Hence, it follows from (2.4) and (3.7) that there exists $(\mu _{n})\subset \partial J_{p,\beta }(u_{n})$ such that

\[ \|\mu_{n}\|_{*}=\Lambda_{J_{p,\beta}}(u_{n})=o_{n}(1) \mbox{ and } \mu_{n}=Q'_p(u_{n})-\rho_{n}, \]

where $\rho _{n}\in \partial \mathcal {F}_\beta (u_{n}).$ Then,

(3.9)\begin{align} \begin{aligned} c + 1 + \| u_n\|_{W_0^{1,p}(\Omega)} & \geq J_{p,\beta}(u_n) - \frac{1}{q}\left\langle \mu_n, u_n \right\rangle + o_n(1)\\ & = J_{p,\beta}(u_n) - \frac{1}{q}\left\langle Q_p'(u_n)-\rho_n, u_n \right\rangle + o_n(1)\\ & = \left(\frac{1}{p}-\frac{1}{q}\right)\| u_n\|^p_{W_0^{1,p}(\Omega)} +\int_{\Omega}\left(\frac{1}{q}\rho_n u_n - F_\beta(u_n)\right) \,{\rm d}x + o_n(1). \end{aligned} \end{align}

Moreover, note that by (3.3) and (3.4), we have

(3.10)\begin{equation} \int_{\Omega}\left(\frac{1}{q}\rho_n u_n - F_{\beta}(u_n)\right) \,{\rm d}x = \frac{\beta}{q}\int_{\{u_n=\beta\}}\rho_n \,{\rm d}x + \frac{\beta^q}{q}|\{u_n > \beta\}| \geq 0. \end{equation}

Hence,

(3.11)\begin{equation} c + 1 + \| u_n\|_{W_0^{1,p}(\Omega)} \geq \left(\frac{1}{p}-\frac{1}{q}\right)\| u_n\|^p_{W_0^{1,p}(\Omega)} + o_n(1),\end{equation}

which implies that the sequence $(u_n)$ is bounded in $W_0^{1,p}(\Omega )$. Thus, by Sobolev embedding theorems, passing to a subsequence if necessary, we obtain

(3.12)\begin{equation} \begin{cases} u_n \rightharpoonup u \text{ in } W_0^{1,p}(\Omega), \ u_n \rightarrow u \ \mbox{ in } \ L^{s}(\Omega), \\ u_n(x) \rightarrow u(x) \ \ \mbox{a.e in} \ \Omega, \\ |u_n(x)| \leq h(x) \ \mbox{ for some } \ h \in L^{s}(\Omega), s\in [1,p^*:=\frac{Np}{N-p}). \end{cases} \end{equation}

Using a similar argument than [13, pg. 1071], we conclude that $J_{p,\beta }$ satisfies the nonsmooth Palais–Smale condition.

Let us define the functional $I_{p,\beta }: W^{1,p}_0(\Omega ) \to \mathbb {R}$, given by

\[ I_{p,\beta}(u) := J_{p,\beta}(u) + \frac{(p-1)}{p}|\Omega|. \]

Note that, by lemma 3.1, lemma 3.2 and theorem 2.2, $I_{p,\beta }$ has a critical point $u_{p,\beta } \in W_{0}^{1,p}(\Omega )$ at the level

\begin{align*} c_{p,\beta}& =\inf_{\gamma\in\Gamma}\max_{t\in[0,1]} I_{p,\beta}(\gamma(t))\;\mbox{ with }\\ \Gamma& =\{\gamma\in C([0,1],W_0^{1,p}(\Omega)): \gamma(0)=0\;\mbox{and}\;\gamma(1)=e\}, \end{align*}

that is,

(3.13)\begin{equation} 0\in \partial I_{p,\beta}(u_{p,\beta}) \mbox{ and } I_{p,\beta}(u_{p,\beta}) = c_{p,\beta}. \end{equation}

Hence, there exists $\rho _{p,\beta } \in L^{\frac {q}{q-1}}(\Omega )$ such that $u_{p,\beta }$ and $\rho _{p,\beta }$ satisfy (3.2) and (3.3). Moreover, testing (3.2) with $\varphi = u_{p,\beta }^-:=\min \{u_{p,\beta },\,0\}$ and using (3.3) we have $\|u^{-}_{p,\beta }\|^p_{W^{1,p}_0(\Omega )}=0,$ which implies that $u_{p,\beta }(x)\geq 0$ a.e. in $\Omega.$

Lemma 3.3 Let $u_{p,\beta }$ be given in (3.13). Then the family $(u_{p,\beta })_{1 < p < \overline {p}}$ is bounded in $BV(\Omega ).$

Proof. By Young's inequality, we have

\[ \int_{\Omega}|\nabla u|^{p_1}\,{\rm d}x\leq\frac{p_1}{p_2}\int_{\Omega}|\nabla u|^{p_2}\,{\rm d}x+\frac{p_2-p_1}{p_2}|\Omega|, \mbox{ for all } 1< p_1\leq p_2, u\in W_0^{1,p}(\Omega). \]

Hence, $I_{p,\beta }$ is nondecreasing with respect to $p$ and arguing as in [32], we conclude that $(I_{p,\beta }(u_{p,\beta }))_{1< p<\overline {p}}$ is increasing. Hence,

(3.14)\begin{equation} c_{p_1}\leq c_{p_2}\end{equation}

for all $1 < p_1\leq p_2.$ Note also that, by (3.13),

\begin{align*} c_{p,\beta}& =I_{p,\beta}(u_{p,\beta})-\frac{1}{q} \left\langle Q_p'(u_{p,\beta})-\rho_{p,\beta}, u_{p,\beta} \right\rangle \\ & =\left(\frac{1}{p}-\frac{1}{q}\right)\int_{\Omega}| \nabla u_{p,\beta}|^p\,{\rm d}x +\int_{\Omega}\left(\frac{1}{q}\rho_{p,\beta} u_{p,\beta} - F_\beta(u_{p,\beta})\right)\,{\rm d}x . \end{align*}

From (3.10) and (3.14), it follows that

(3.15)\begin{equation} \int_{\Omega}|\nabla u_{p,\beta}|^p \,{\rm d}x\leq C, \mbox{ for all } 1< p<\overline{p},\end{equation}

where $C:=\frac {\overline {p}q}{q-\overline {p}}c_{\overline {p},\,\beta }>0$ is a constant independent of $p\in (1,\,\overline {p}).$

Applying once more Young's inequality, we obtain

\begin{align*} \|u_{p,\beta}\| & \leq \frac{1}{p}\int_\Omega|\nabla u_{p,\beta}|^{p}\,{\rm d}x + \frac{p-1}{p}|\Omega|\\ & \leq \overline{C}+ |\Omega|, \end{align*}

for some constant $\overline {C}>0,$ independent of $p.$

Lemma 3.4 For each $\beta >0,$ the function $u_{p,\beta }$ given in (3.13) satisfies

(3.16)\begin{equation} \|u_{p,\beta}\|_{L^\infty(\Omega)}\leq \overline{C},\end{equation}

for some constant $\overline {C}>0$ independent of $p\in (1,\,\overline {p}).$

Proof. Here to simplify the notation we put $u=u_{p,\beta }$ and $\rho _{p,\beta }=\rho.$ To obtain the $L^\infty$-estimate we will use the Moser's iteration [31] and a careful analysis of some constants. For each $L>0$, we define

\begin{align*} u_L(x)& := \left\{ \begin{array}{@{}rcl} u(x), & \mbox{if} & u(x)\leq L\\ L, & \mbox{if} & u(x)> L, \end{array} \right.\\ z_{L,n}(x)& :=(u_L^{p(\gamma-1)}u)(x)\ \mbox{ and }\ w_L(x):=(uu_L^{\gamma-1})(x), \end{align*}

with $\gamma >1$ to be determined later. Choosing $\varphi =z_{L,n}$ in (3.2), we get

\[ \int_{\Omega}u_L^{p(\gamma-1)}|\nabla u|^{p}\,{\rm d}x\displaystyle={-}p(\gamma-1)\int_{\Omega}u_L^{p\gamma-p-1}u|\nabla u|^{p-2}\nabla u\nabla u_L \,{\rm d}x+\int_{\Omega}\rho u u_L^{p(\gamma-1)}\,{\rm d}x. \]

Since

\[ p(\gamma-1)\int_{\Omega}u_L^{p\gamma-p-1}u|\nabla u|^{p-2}\nabla u\nabla u_L \,{\rm d}x=p(\gamma-1)\int_{\{u\leq L\}}u_L^{p(\gamma-1)}|\nabla u|^p\,{\rm d}x\geq0 \]

and $0\leq \rho (x)\leq |u(x)|^{q-1}$ for almost every $x\in \Omega,$ see (3.3), we obtain

(3.17)\begin{equation} \int_{\Omega}u_L^{p(\gamma-1)}|\nabla u|^{p}\,{\rm d}x\leq \int_{\Omega}u^qu_L^{p(\gamma-1)}\,{\rm d}x. \end{equation}

On the other hand, by (3.8) it follows that

\[ |w_L|_{L^{p^*}(\Omega)}^{p}\leq c_{p,\beta}\int_{\Omega}|\nabla w_L|^{p}\,{\rm d}x =c_{p,\beta}\int_{\Omega} |\nabla(uu_L^{\gamma-1})|^{p}\,{\rm d}x, \]

where $c_{p,\beta }=\bigl (p(N-1)/(N-p)\bigl )^{p}.$ Thus,

\[ |w_L|_{L^{p^*}(\Omega)}^{p}\leq 2^pc_{p,\beta}\int_{\Omega}u_L^{p(\gamma-1)}|\nabla u|^p\,{\rm d}x+2^pc_{p,\beta}(\gamma-1)^{p}\int_{\Omega}u_L^{p(\gamma-2)}u^p|\nabla u_L|^p \,{\rm d}x, \]

hence, we get

(3.18)\begin{equation} |w_L|_{L^{p^*}(\Omega)}^p\leq 2^pc_{p,\beta}\gamma^p\int_{\Omega}u_L^{p(\gamma-1)}|\nabla u|^p\,{\rm d}x. \end{equation}

Combining (3.17) and (3.18), we obtain

\[ |w_L|_{L^{p^*}(\Omega)}^p\leq 2^pc_{p,\beta}\gamma^p\int_{\Omega}u^{q-p}(uu_L^{\gamma-1})^p\,{\rm d}x, \]

and so,

\[ |w_L|_{L^{p^*}(\Omega)}^{p}\leq 2^pc_{p,\beta} \gamma^p\int_{\Omega}u^{q-p}w_L^p\,{\rm d}x. \]

Now we use the Hölder's inequality (with exponents $p^*/(q-p)$ and $p^*/(p^*-(q-p))$ to get that

\[ |w_L|_{L^{p^*}(\Omega)}^p\leq 2^pc_{p,\beta}\gamma^p\Biggl(\int_{\Omega}u^{p^*}\,{\rm d}x\Biggl)^{\frac{q-p}{p^*}}\Biggl(\int_{\Omega}w_L^{\frac{pp^*}{p^*-(q-p)}}\,{\rm d}x\Biggl)^{\frac{p^*-(q-p)}{p^*}}, \]

where $p<\frac {pp^*}{p^*-(q-p)}< p^*.$

The previous inequality, (3.8) and (3.15) imply that

(3.19)\begin{equation} |w_L|_{L^{p^*}(\Omega)}^{p}\leq (2\theta_p)^p\gamma^p\Biggl(\int_{\Omega}w_L^{\alpha^*}\,{\rm d}x\Biggl)^{\frac{p}{\alpha^*}}, \end{equation}

where

(3.20)\begin{equation} \alpha^*:=\frac{pp^*}{p^*-(q-p)}\ \mbox{ and } \ \theta_p:=\biggl(p\frac{(N-1)}{(N-p)}\biggl)^{\frac{q}{p}}C^{\frac{q-p}{p}}, \end{equation}

with the constant $C$ given in (3.15).

Using that $0\leq w_L=(uu_L^{\gamma -1})\leq u^{\gamma }$ on the right-hand side of (3.19) and then letting $L\rightarrow \infty$ on the left-hand side, as a consequence of Fatou's Lemma on the variable $L$, we have

\[ \Biggl(\int_{\Omega}u^{p^*\gamma}\,{\rm d}x\Biggl)^{\frac{p}{p^*}}\leq (2\theta_p)^p\gamma^p\Biggl(\int_{\Omega}u^{\gamma\alpha^*}\,{\rm d}x\Biggl)^{\frac{p}{\alpha^*}}, \]

from which we get that

(3.21)\begin{equation} |u|_{L^{p^*\gamma}(\Omega)}\leq(2\theta_p)^{\frac{1}{\gamma}}\gamma^{\frac{1}{\gamma}}|u|_{L^{\gamma\alpha^*}(\Omega)}. \end{equation}

Let us define $\sigma :=p^*/\alpha ^*.$ When $\gamma =\sigma$ in (3.21), since $\gamma \alpha ^*=p^*$ we have $u\in L^{p^*\sigma }(\Omega )$ and

(3.22)\begin{equation} |u|_{L^{p^*\sigma}(\Omega)}\leq (2\theta_p)^{\frac{1}{\sigma}}\sigma^{\frac{1}{\sigma}} |u|_{L^{p^*}(\Omega)}. \end{equation}

Now, choosing $\gamma =\sigma ^2$ in (3.21), since $\gamma \alpha ^*=p^*\sigma$ and $p^*\gamma =p^*\sigma ^2,$ we obtain

(3.23)\begin{equation} |u|_{L^{p^*\sigma^2}(\Omega)}\leq (2\theta_p)^{\frac{1}{\sigma^2}}\sigma^{\frac{2}{\sigma^2}} |u|_{L^{p^*\sigma}(\Omega)}, \end{equation}

by using (3.22) and (3.23), we have

\[ |u|_{L^{p^*\sigma^2}(\Omega)}\leq(2\theta_p)^{\frac{1}{\sigma^2}+\frac{1}{\sigma}} \sigma^{\frac{2}{\sigma^2}+{\frac{1}{\sigma}}} |u|_{L^{p^*}(\Omega)}. \]

For $n\geq 1,$ we define $\sigma _n$ inductively so that $\sigma _n=\sigma ^n.$ Then, from (3.21), it follows that

(3.24)\begin{equation} |u|_{L^{p^*\sigma^n}(\Omega)}\leq (2\theta_p)^{\frac{1}{\sigma^n}+\cdots+\frac{1}{\sigma^2}+\frac{1}{\sigma}} \sigma^{\frac{n}{\sigma^n}+\cdots+\frac{2}{\sigma^2}+{\frac{1}{\sigma}}} |u|_{L^{p^*}(\Omega)}. \end{equation}

Note that

\[ \displaystyle\sum_{i=1}^{\infty}\frac{1}{\sigma^i}=\frac{1}{\sigma-1} \ \mbox{ and } \displaystyle\sum_{i=1}^{\infty}\frac{i}{\sigma^i}=\frac{\sigma}{(\sigma-1)^2}. \]

Thus, since $\sigma >1,$ passing to the limit as $n\rightarrow \infty$ in (3.24) we conclude that $u\in L^{\infty }(\Omega )$ and

(3.25)\begin{equation} |u|_{L^\infty(\Omega)}\leq (2\theta_p)^{\frac{1}{\sigma-1}}\sigma^{\frac{\sigma}{(\sigma-1)^2}}|u|_{L^{p^*}(\Omega)}. \end{equation}

Finally, since $\sigma =\frac {N}{N-p}-\frac {q}{p}+1$ and $1< p< q<1^*< p^*,$ using once more (3.8), the expression of $\theta _p$ (see (3.20)) and (3.25) we conclude the proof of the lemma.

As a consequence of lemma 3.3 and the compactness of the embedding $BV(\Omega )\hookrightarrow L^r(\Omega )$, for $r\in [1,\,1^*)$ (where $1^* := N/(N-1)$), it follows that there exists $u_\beta \in BV(\Omega )$ such that, as $p \to 1^+,$

(3.26)\begin{equation} u_{p,\beta} \to u_\beta \quad \mbox{ in } L^r(\Omega)\end{equation}

and

(3.27)\begin{equation} u_{p,\beta}(x) \to u_\beta(x) \mbox{ a.e. in } \Omega.\end{equation}

Hence, according to lemma 3.4 we have $u_\beta \in L^\infty (\Omega )$ and $u_\beta (x)\geq 0$ for almost every $x\in \Omega.$

In what follows, we will prove that $u_\beta$ is a solution of (1.1), in the sense of definition (1.2). Furthermore, we will prove that $u_\beta \not \equiv 0.$

We start with the following result:

Lemma 3.5 Let $u_{p,\beta } \in W^{1,p}_0(\Omega ),$ $\rho _{p,\beta } \in L^{\frac {q}{q-1}}(\Omega )$ and $u_\beta \in BV(\Omega )$ satisfying (3.2), (3.3) and (3.26). Then, there exists $\rho _{\beta } \in L^{\frac {q}{q-1}}(\Omega ),$ such that

(3.28)\begin{equation} \rho_{p,\beta} \rightharpoonup \rho_{\beta} \mbox{ in } L^{\frac{q}{q-1}}(\Omega), \mbox{ as p } \to 1^+.\end{equation}

Moreover, $\rho _{\beta }$ satisfies, for almost every $x\in \Omega,$

(3.29)\begin{equation} \rho_{\beta}(x) \in \begin{cases} \{0\}, & \ \mbox{if} \ u_\beta(x)<\beta,\\ [0, \beta^{q-1}], & \ \mbox{if} \ u_\beta(x)=\beta,\\ \{u_\beta(x)^{q-1}\}, & \ \mbox{if} \ u_\beta(x)>\beta. \end{cases}\end{equation}

Proof. By lemma 3.4, it follows that $(\rho _{p,\beta })_{1 < p < \overline {p}}$ is bounded in $L^{\frac {q}{q-1}}(\Omega )$. Hence, there exists $\rho _{\beta } \in L^{\frac {q}{q-1}}(\Omega )$, such that (3.28) holds. Moreover, if $E \subset \Omega$ is a measurable set, then

(3.30)\begin{equation} \int_E \rho_{p,\beta} \,{\rm d}x = \int_\Omega \rho_{p,\beta} . \chi_E \,{\rm d}x \to \int_\Omega \rho_{\beta} . \chi_E \,{\rm d}x= \int_E \rho_{\beta} \,{\rm d}x, \mbox{ as } p \to 1^+. \end{equation}

Now, let us show that $\rho _\beta$ satisfies (3.29). First of all, note that

(3.31)\begin{equation} 0 \leq \rho_\beta(x), \quad \mbox{a.e. in } \Omega. \end{equation}

Indeed, otherwise, a measurable set $E \subset \Omega$ would exist, such that $\rho _\beta (x) < 0$, in $E$. Then,

\[ \int_E \rho_\beta \,{\rm d}x < 0. \]

Hence, from (3.30), we have a contradiction with the fact that $\rho _{p,\beta }(x) \geq 0$, for all $p > 1$.

Now let us show that

(3.32)\begin{equation} \rho_\beta(x) = 0, \quad \mbox{if}\ u_\beta(x) < \beta. \end{equation}

Let $E = [u_\beta < \beta ]$ and note that

(3.33)\begin{align} 0 & \leq \int_E \rho_{p,\beta} \,{\rm d}x \\ & =\int_{E \cap [u_{p,\beta} \geq \beta]}\rho_{p,\beta} \,{\rm d}x\nonumber\\ & \leq \int_{E \cap [u_{p,\beta} \geq \beta]}u_{p,\beta}^{q-1} \,{\rm d}x \nonumber \end{align}

Claim 1: $\displaystyle \int _{E \cap [u_{p,\beta } \geq \beta ]}u_{p,\beta }^{q-1} \,{\rm d}x = o_p(1)$.

Assuming for a while that claim 1 holds true, then from (3.30), (3.31) and (3.33), it follows that (3.32) holds.

Now, let us show that the claim holds. First of all, let us show that

(3.34)\begin{equation} \chi_{[u_{p,\beta} \geq \beta]} \to 0, \quad \mbox{a.e. in}\ E,\ \mbox{as}\ p \to 1^+. \end{equation}

Indeed, let us suppose by contradiction that there exists $E^* \subset E$ with positive measure such that, for every fixed $x \in E^*$, there exists $(p_{n,x})_{n \in \mathbb {N}}$, such that $p_{n,x} \to 1^+$, as $n \to +\infty$ and

\[ \chi_{[u_{p_{n,x},\beta} \geq \beta]}(x) = 1, \quad \mbox{for all}\ n \in \mathbb{N}. \]

This, in turn, is equivalent to

(3.35)\begin{equation} u_{p_{n,x}}(x) \geq \beta, \quad \mbox{for all}\ n \in \mathbb{N}.\end{equation}

By doing $n \to +\infty$ in (3.35), since $p_{n,x} \to 1^+$, we have that

\[ u_\beta(x) \geq \beta, \quad \mbox{for all}\ x \in E^*. \]

But this contradicts the fact that $E^* \subset E$. Hence (3.34) holds.

Therefore, from (3.34) and the Lebesgue Convergence Theorem, it follows that claim 1 holds.

Now let us show that

(3.36)\begin{equation} \rho_\beta(x) = u_\beta^{q-1}(x), \quad \mbox{if}\ u_\beta(x) > \beta. \end{equation}

For this, let us define $E = [u_\beta > \beta ]$. Note that

(3.37)\begin{equation} \int_E \rho_{p,\beta} \,{\rm d}x = \int_{E \cap [u_{p,\beta} = \beta]}\rho_{p,\beta} \,{\rm d}x + \int_{E \cap [u_{p,\beta} > \beta]}u_{p,\beta}^{q-1} \,{\rm d}x. \end{equation}

As in (3.34), we can prove that

(3.38)\begin{equation} \chi_{[u_{p,\beta} = \beta]} \to 0, \quad \mbox{a.e. in}\ E,\ \mbox{as}\ p \to 1^+. \end{equation}

Then, from (3.38) and Lebesgue Convergence Theorem,

(3.39)\begin{equation} \int_{E \cap [u_{p,\beta} = \beta]}\rho_{p,\beta} \,{\rm d}x \leq \beta^{q-1} \int_E \chi_{[u_{p,\beta} = \beta]} \to 0, \quad \mbox{as}\ p \to 1^+. \end{equation}

On the other hand, since

\[ \int_{E \cap [u_{p,\beta} > \beta]}u_{p,\beta}^{q-1} \,{\rm d}x = \int_{E} u_{p,\beta}^{q-1}\chi_{[u_{p,\beta} > \beta]} \,{\rm d}x, \]

we have from (3.26) and the fact that $\chi _{[u_{p,\beta } > \beta ]} \to 1$, a.e. in $E$, as $p \to 1^+$, that

(3.40)\begin{equation} \int_{E \cap [u_{p,\beta} > \beta]}u_{p,\beta}^{q-1} \,{\rm d}x \to \int_{E} u_\beta^{q-1} \,{\rm d}x. \end{equation}

Then, from (3.37), (3.39) and (3.40), it follows that

(3.41)\begin{equation} \int_E \rho_{p,\beta} \,{\rm d}x \to \int_{E} u_\beta^{q-1} \,{\rm d}x, \quad \mbox{as} p \to 1^+. \end{equation}

Hence, from (3.30) and (3.41), we have that

(3.42)\begin{equation} \int_E \rho_\beta \,{\rm d}x = \int_E u_\beta^{q-1} \,{\rm d}x \end{equation}

Claim 2: $\rho _\beta (x) \leq u_\beta ^{q-1}(x)$ in $[u_\beta \geq \beta ]$.

Assuming that claim 2 holds, it follows from (3.42) that

\[ \rho_\beta(x) = u_\beta^{q-1}(x), \quad \mbox{in}\ E \]

and

\[ \rho_\beta(x) \in [0,\beta^{q-1}], \quad \mbox{in}\ [u_\beta = \beta] \]

and we are done.

In order to prove claim 2, let us assume by contradiction that there exists $E_* \subset [u_\beta \geq \beta ]$, with positive measure and such that

\[ \rho_\beta > u_\beta ^{q-1}, \quad \mbox{in}\ E_*. \]

Then,

(3.43)\begin{equation} \int_{E_*} \rho_\beta \,{\rm d}x > \int_{E_*} u_\beta^{q-1} \,{\rm d}x . \end{equation}

Then, from (3.26) and (3.30), there exists $p_n \to 1^+$, as $n \to +\infty$, such that

\[ \int_{E_*} \rho_{p_n,\beta} \,{\rm d}x > \int_{E_*} u_{p_n,\beta}^{q-1} \,{\rm d}x, \]

which contradicts the fact that $\rho _{p,\beta }(x) \leq u_{p,\beta }^{q-1}(x)$, a.e. in $\Omega$.

Then claim 2 holds and this finishes the proof.

Lemma 3.6 For each $\beta >0,$ there exists a vector field $\textbf {z}_{\beta } \in L^\infty (\Omega,\,\mathbb {R}^N)$ such that $\|\textbf {z}_{\beta }\|_\infty \leq 1$ and

(3.44)\begin{equation} {-}\mbox{div}\, \textbf{z}_{\beta}= \rho_{\beta}, \quad \mbox{in}\ \mathcal{D}'(\Omega),\end{equation}

with $\rho _{\beta }$ satisfying (3.29).

Proof. The inequality (3.15) implies that (see [8, proposition 3] or [29, theorem 3.3]) there exists $\textbf {z}_{\beta } \in L^\infty (\Omega,\,\mathbb {R}^N)$, such that $\|\textbf {z}_{\beta }\|_\infty \leq 1$ and

(3.45)\begin{equation} |\nabla u_{p,\beta}|^{p-2}\nabla u_{p,\beta} \rightharpoonup \textbf{z}_{\beta} \mbox{ weakly in } L^r(\Omega,\mathbb{R}^N), \mbox{ as } p \to 1^+,\end{equation}

for all $1 \leq r < \infty$. In particular, as $p \to 1^+$,

(3.46)\begin{equation} |\nabla u_{p,\beta}|^{p-2}\nabla u_{p,\beta} \to \mbox{div}\, \textbf{z}_{\beta} \quad \mbox{in}\ \mathcal{D}'(\Omega).\end{equation}

Therefore, by using (3.2), (3.28) and (3.46) and the Lebesgue dominated convergence theorem, we conclude that

\[ -\mbox{div}\, \textbf{z}_{\beta} = \rho_{\beta}, \quad \mbox{in}\ \mathcal{D}'(\Omega), \]

which proves the lemma.

Lemma 3.7 The function $u_\beta$ and the vector field $\textbf {z}_{\beta }$ satisfy the following equality in the sense of measures in $\Omega,$

\[ (\textbf{z}_{\beta},D u_\beta) = |D u_\beta|. \]

Proof. First of all, since $\|\textbf {z}_{\beta }\|_\infty \leq 1$, it follows that, $(\textbf {z}_{\beta },\,Du_\beta ) \leq |Du_\beta |$ in $\mathcal {M}(\Omega )$. In fact, for any Borel set $B$, by (2.1),

\begin{align*} \int_B (\textbf{z}_{\beta},Du_\beta) & \leq \left| \int_B (\textbf{z}_{\beta},Du_\beta) \right|\\ & \leq \|\textbf{z}_{\beta}\|_\infty \int_B |Du_\beta|\\ & \leq \int_B |Du_\beta|. \end{align*}

Hence, it is enough to show the opposite inequality, i.e., that for all $\varphi \in C^1_0(\Omega )$, $\varphi \geq 0$,

(3.47)\begin{equation} \langle (\textbf{z}_{\beta}, Du_\beta), \varphi \rangle \geq \int_\Omega \varphi |Du_\beta|.\end{equation}

In order to do so, let us consider $u_{p,\beta } \varphi \in W^{1,p}(\Omega )$ as a test function in (3.1). Thus we obtain,

(3.48)\begin{equation} \int_\Omega \varphi |\nabla u_{p,\beta}|^p \,{\rm d}x + \int_\Omega u_{p,\beta}|\nabla u_{p,\beta}|^{p-2}\nabla u_{p,\beta} \cdot \nabla \varphi \,{\rm d}x = \int_\Omega \rho_{p,\beta} \varphi \,{\rm d}x.\end{equation}

Now we shall calculate the lower limit as $p \to 1^+$ in both sides of (3.48). Before it, note that, Young's inequality and the lower semicontinuity of the map $v \mapsto \displaystyle \int _\Omega \varphi |Dv|$ with respect to the $L^r(\Omega )$ convergence, imply that

\begin{align*} \int_\Omega \varphi |Du_\beta| & \leq \liminf_{p \to 1^+} \int_\Omega \varphi |\nabla u_{p,\beta}| \,{\rm d}x\\ & \leq \liminf_{p \to 1^+}\left( \frac{1}{p} \int_\Omega \varphi |\nabla u_{p,\beta}|^p \,{\rm d}x + \frac{p-1}{p}\int_\Omega \varphi \,{\rm d}x \right)\\ & = \liminf_{p \to 1^+} \int_\Omega \varphi |\nabla u_{p,\beta}|^p \,{\rm d}x. \end{align*}

Moreover, by (3.46), it follows that

(3.49)\begin{equation} \lim_{p \to1^+}\int_\Omega u_{p,\beta}|\nabla u_{p,\beta}|^{p-2}\nabla u_{p,\beta} \nabla \varphi \,{\rm d}x = \int_\Omega u_\beta \textbf{z}_{\beta}\cdot \nabla \varphi \,{\rm d}x.\end{equation}

Finally, Lebesgue's dominated convergence theorem and (3.26) imply that

(3.50)\begin{equation} \lim_{p \to 1^+}\int_\Omega \rho_{p,\beta} \varphi \,{\rm d}x = \int_\Omega \rho_{\beta} \varphi \,{\rm d}x.\end{equation}

Then, from (3.44), (3.48), (3.49) and (3.50), it follows that

\begin{align*} \langle (\textbf{z}_{\beta}, Du_\beta), \varphi\rangle & ={-}\int_\Omega \varphi u_\beta \mbox{div}\textbf{z}_{\beta} - \int_\Omega u_\beta \textbf{z}_{\beta}\cdot\nabla \varphi \,{\rm d}x\\ & = \int_\Omega \rho_{\beta} u_\beta \varphi \,{\rm d}x - \int_\Omega u_\beta \textbf{z}_{\beta}\cdot\nabla \varphi \,{\rm d}x\\ & = \lim_{p \to 1^+}\left(\int_\Omega \rho_{p,\beta} u_{p,\beta} \varphi \,{\rm d}x - \int_\Omega u_{p,\beta}|\nabla u_{p,\beta}|^{p-2}\nabla u_{p,\beta} \cdot\nabla \varphi \,{\rm d}x\right)\\ & = \liminf_{p \to 1^+}\int_\Omega \varphi|\nabla u_{p,\beta}|^p \,{\rm d}x\\ & \geq \int_\Omega \varphi |Du_\beta|. \end{align*}

Then, (3.47) holds and this finishes the proof.

Lemma 3.8 The function $u_\beta$ satisfies $[\textbf {z}_{\beta },\,\nu ] \in \mbox {sign}(-u_\beta )$ on $\partial \Omega$.

Proof. To check that $[\textbf {z}_{\beta },\,\nu ]\in sign(-u_\beta )$ it is enough to show that

(3.51)\begin{equation} \int_\Omega (| u_\beta | + u_\beta[\textbf{z}_{\beta},\nu])d\mathcal{H}^{N-1} = 0.\end{equation}

Indeed, since

\begin{align*} -u_\beta[\textbf{z}_{\beta},\nu] & \leq \| \textbf{z}_{\beta} \|_{L^{\infty}(\Omega)}| u_\beta | \\ & \leq | u_\beta |, \end{align*}

the integrand in (4.18) is nonnegative. Then, (4.18) holds if and only if $[\textbf {z}_{\beta },\,\nu ](-u_\beta ) = |u_\beta |$ $\mathcal {H}^{N-1}$a.e. on $\partial \Omega$.

In order to verify (4.18), let us consider $(u_{p,\beta } - \varphi ) \in W^{1,p}_{0}(\Omega )$ as test function in (3.1) with $\varphi \in C^1_{0}(\Omega )$. Then we get

(3.52)\begin{equation} \int_\Omega |\nabla u_{p,\beta}|^p \,{\rm d}x = \int_\Omega |\nabla u_{p,\beta}|^{p-2}\nabla u_{p,\beta} \nabla \varphi \,{\rm d}x + \int_\Omega \rho_{p,\beta} (u_{p,\beta} - \varphi)\,{\rm d}x.\end{equation}

From Young's inequality, Green's Formula, (3.44), (3.46), lemma 3.7 and (3.52), we have that, as $p \to 1^+$,

(3.53)\begin{align} p \int_\Omega |\nabla u_{p,\beta}| \,{\rm d}x & \leq \int_\Omega |\nabla u_{p,\beta}|^p \,{\rm d}x + (p-1)|\Omega|\nonumber\\ & =\int_\Omega |\nabla u_{p,\beta}|^{p-2}\nabla u_{p,\beta} \nabla \varphi \,{\rm d}x + \int_\Omega \rho_{p,\beta}(u_{p,\beta} - \varphi)\,{\rm d}x + (p-1)|\Omega|\nonumber\\ & =\int_\Omega \textbf{z}_{\beta}\cdot \nabla \varphi \,{\rm d}x + \int_\Omega \rho_{\beta}(u_\beta - \varphi)\,{\rm d}x + o_p(1)\nonumber\\ & ={-}\int_\Omega \varphi \mbox{div}\textbf{z}_{\beta} -\int_\Omega \rho_{\beta} \varphi \,{\rm d}x + \int_\Omega \rho_{\beta} u_\beta \,{\rm d}x + o_p(1)\nonumber\\ & = \int_\Omega \rho_{\beta} u_\beta \,{\rm d}x + o_p(1)\nonumber\\ & ={-}\int_\Omega u_\beta \mbox{div}\textbf{z}_{\beta} + o_p(1)\nonumber\\ & =\int_\Omega (\textbf{z}_{\beta}, Du_\beta) - \int_{\partial \Omega} \left[\textbf{z}_{\beta},\nu \right] u_\beta d\mathcal{H}^{N-1} + o_p(1)\nonumber\\ & =\int_\Omega |Du_\beta| - \int_{\partial \Omega} \left[\textbf{z}_{\beta},\nu \right] u_\beta d\mathcal{H}^{N-1} + o_p(1). \end{align}

Hence, from (3.53) and the lower semicontinuity of the norm in $BV(\Omega )$, it follows that

(3.54)\begin{equation} \int_{\partial B}\left(|u_\beta| + \left[\textbf{z}_{\beta},\nu \right] u_\beta \right) d\mathcal{H}^{N-1} \leq 0.\end{equation}

But the last inequality implies in (4.18) and we are done.

Now, let us prove that the function $u_\beta \in BV(\Omega )\cap L^\infty (\Omega )$ is a nonnegative and nontrivial solution of (1.1), in the sense of the definition (1.2).

First of all, note that by lemmas 3.6, 3.7 and 3.8, $u_\beta \in BV(\Omega ),$ $\rho _{\beta }\in L^{\frac {q}{q-1}}(\Omega )$ and $\textbf {z}_{\beta }\in L^{\infty }(\Omega,\,\mathbb {R}^N)$ satisfy (1.2) and (1.3). Moreover, since $u_{p,\beta }(x)\geq 0$ for almost every $x\in \Omega,$ according to (3.27) and lemma 3.4, it follows that $u_\beta \in L^{\infty }(\Omega )$ and $u_\beta (x)\geq 0$ for almost every $x\in \Omega.$

Now let us show that $u_\beta \not \equiv 0.$ Invoking lemma 3.1 and (3.13), we have

(3.55)\begin{align} \alpha + o_p(1) \leq c_{p,\beta}=I_{H,p}(u_{p,\beta})\leq \frac{1}{p}\int_{\Omega}|\nabla u_{p,\beta}|^p \,{\rm d}x + o_p(1). \end{align}

Hence, since $\alpha$ is independent of $p$ (see lemma 3.1), (3.2), (3.26), (3.28), and Lebesgue's dominated convergence theorem, imply that

(3.56)\begin{equation} \alpha\leq\lim_{p\rightarrow1^+}\frac{1}{p}\int_{\Omega}|\nabla u_{p,\beta}|^p \,{\rm d}x=\lim_{p\rightarrow1^+}\frac{1}{p}\int_{\Omega}\rho_{p,\beta}u_{p,\beta} \,{\rm d}x=\int_{\Omega}\rho_{\beta}u_\beta \,{\rm d}x. \end{equation}

Thus, combining (3.44), Green's Formula (see (2.3)), lemma 3.7, lemma 3.8 and (3.56), we deduce that

\begin{align*} 0& < \alpha \\ & \leq \int_{\Omega}(\textbf{z}_{\beta},Du_\beta) - \int_{\partial\Omega}[\textbf{z}_\beta,\nu]u_\beta\;d\mathcal{H}^{N-1}\\ & =\int_{\Omega}|Du_\beta| - \int_{\partial\Omega}[ \textbf{z}_\beta,\nu]u_\beta\;d\mathcal{H}^{N-1}\\ & = \int_{\Omega}|Du_\beta| + \int_{\partial\Omega}|u_\beta|\;d\mathcal{H}^{N-1}\\ & = \|u_\beta\|, \end{align*}

thus $u_\beta \not \equiv 0$. Then theorem 1.1 is proved.

4. Proof of theorem 1.2

Now, let us perform a deep analysis of the behaviour of $u_{p,\beta }$, as $\beta \to 0^+$.

For each $\beta > 0$, let us define the functional $I_\beta : BV(\Omega ) \to \mathbb {R}$, given by

\[ I_\beta (u) = \int_{\Omega}|Du| + \int_{\partial \Omega}|u| d\mathcal{H}^{N-1} - \int_\Omega F_\beta(u) \,{\rm d}x. \]

Note that, since ${\bf z}_{\beta }$ and $u_\beta$ satisfy

(4.1)\begin{equation} \left\{ \begin{array}{@{}rcl} - \mbox{div}\, {\textbf z}_{\beta} & = & \rho_{\beta} \quad \mbox{in}\ \mathcal{D}'(\Omega),\\ ({\textbf z}_{\beta},Du_\beta) & = & |Du_\beta| \quad \mbox{in}\ \mathcal{M}(\Omega),\\ {[{\textbf{z}_{\beta}},\nu]} & \in & sign({-}u_\beta) \quad \mathcal{H}^{N-1}-\mbox{a.e. on}\ \partial \Omega, \end{array} \right. \end{equation}

by taking $u_\beta$ as test function in (4.1) and using Green's Formula, (3.1) and (3.28), it follows that

(4.2)\begin{align} \|u_\beta\| & = \int_\Omega |Du_\beta| + \int_{\partial \Omega}|u_\beta| d\mathcal{H}^{N-1}\nonumber\\ & ={-}\int_\Omega u_\beta\mbox{div}\, {\textbf{z}_{\beta}}\nonumber\\ & = \int_\Omega u_\beta\rho_{\beta} \,{\rm d}x\\ & =\int_\Omega u_{p,\beta}\rho_{p,\beta} \,{\rm d}x + o_p(1)\nonumber\\ & =\int_\Omega |\nabla u_{p,\beta}|^p \,{\rm d}x + o_p(1). \nonumber \end{align}

Moreover, from (3.26) and (3.27), it follows that

(4.3)\begin{equation} \int_\Omega F_\beta(u_\beta) \,{\rm d}x = \int_\Omega F_\beta(u_{p,\beta}) \,{\rm d}x + o_p(1). \end{equation}

Hence, from (4.2) and (4.3), we have that

(4.4)\begin{equation} I_{\beta}(u_\beta) = I_{p,\beta}(u_{p,\beta}) + o_p(1). \end{equation}

Since we are interested in the behaviour of $u_\beta$, as $\beta \to 0^+$, let us assume from now on that $0 < \beta < \beta _0$.

Lemma 4.1 The family $(u_\beta )_{0 < \beta < \beta _0}$ is bounded in $BV(\Omega )$.

Proof. First of all, let us prove that, if $0 < \beta _1 < \beta _2 < \beta _0$, then

(4.5)\begin{equation} I_{\beta_1}(u_{\beta_1}) \leq I_{\beta_2}(u_{\beta_2}). \end{equation}

In order to do so, let us prove that, for $p > 1$ fixed,

(4.6)\begin{equation} I_{p,\beta_1}(u_{p,\beta_1}) < I_{p,\beta_2}(u_{p,\beta_2}). \end{equation}

Note that, for $u \in W^{1,p}_0(\Omega )$, since $F_{\beta _1}(u) \geq F_{\beta _2}(u)$ a.e. in $\Omega$, it follows that

(4.7)\begin{equation} I_{p,\beta_1}(u) \leq I_{p,\beta_2}(u). \end{equation}

Moreover, let us assume that the function $e$ in lemma 3.1, is $e(\beta _0)$, i.e., that satisfies $I_{p,\beta _0}(e) < p/(p-1)$. Hence, from (4.7), we have that

\[ I_{p,\beta}(e) \leq I_{p,\beta_0}(e) < \frac{p}{p-1}, \]

for all $0 < \beta < \beta _0$. Hence, in the definition of $c_{p,\beta }$, for $0 < \beta < \beta _0$, we can assume without loss of generality that $e = e(\beta _0)$ and then the class of paths $\Gamma$ does not depend on $\beta$. Then, from (4.7), it follows that

\begin{align*} I_{p,\beta_1}(u_{p,\beta_1}) & = c_{p,\beta_1}\\ & =\inf_{\gamma \in \Gamma}\sup_{t \in [0,1]} I_{p,\beta_1}(\gamma(t))\\ & \leq \inf_{\gamma \in \Gamma}\sup_{t \in [0,1]} I_{p,\beta_2}(\gamma(t))\\ & = c_{p,\beta_2}\\ & = I_{p,\beta_2}(u_{p,\beta_2}). \end{align*}

This, in turn, proves (4.6).

Hence, from (4.4), passing the limit as $p \to 1^+$ in (4.6), we have that (4.5) holds.

Then, for all $0 < \beta < \beta _0$,

\[ I_\beta(u_\beta) \leq I_{\beta_0}(u_{\beta_0}) =: C. \]

Note that, by using $u_\beta$ as test function in (4.1), from Green's Formula, we have that

(4.8)\begin{align} \|u_\beta\| & = \int_\Omega |Du_\beta| + \int_{\partial \Omega}|u_\beta| d\mathcal{H}^{N-1}\nonumber\\ & =\int_\Omega ({\bf z}_\beta,Du_\beta) + \int_{\partial \Omega}[{\bf z}_\beta,\nu]u_\beta d\mathcal{H}^{N-1}\nonumber\\ & ={-}\int_\Omega u_\beta \mbox{div}\, {\bf z}_\beta \,{\rm d}x\\ & = \int_\Omega u_\beta \rho_\beta \,{\rm d}x. \nonumber \end{align}

Then, from (3.29), (4.8) and the definition of $F_\beta$, we have that

\begin{align*} I_\beta(u_\beta) & = I_\beta(u_\beta) - \frac{1}{q}\left(\|u_\beta\| - \int_\Omega u_\beta \rho_\beta \,{\rm d}x\right)\\ & =\left(1 - \frac{1}{q}\right)\|u_\beta\| + \int_\Omega \left(\frac{1}{q} u_\beta \rho_\beta - F_\beta(u_\beta)\right) \,{\rm d}x\\ & \geq\left(1 - \frac{1}{q}\right)\|u_\beta\| + \frac{\beta^q}{q}|\{u_\beta > \beta\}|\\ & \geq \left(1 - \frac{1}{q}\right)\|u_\beta\|. \end{align*}

Hence, since $(I_\beta (u_{\beta }))_{0 < \beta < \beta _0}$ is bounded, it follows from the last inequality that $(u_\beta )_{0 < \beta < \beta _0}$ is also bounded.

From the last result, there exists $u_0 \in BV(\Omega )$ such that, for all $r \in [1,\,1^*)$,

(4.9)\begin{equation} u_{\beta} \to u_0 \quad \mbox{ in } L^r(\Omega)\end{equation}

and

(4.10)\begin{equation} u_{\beta}(x) \to u_0(x) \mbox{ a.e. in } \Omega.\end{equation}

Moreover, note that the boundedness on $(u_\beta )_{0 < \beta < \beta _0}$ and (3.29) implies also that $(\rho _\beta )_{0 < \beta < \beta _0}$ is bounded in $L^\frac {q}{q-1}(\Omega )$. Then, as in lemma 3.5, it is possible to show that there exists $\rho _0 \in L^\frac {q}{q-1}(\Omega )$, such that

(4.11)\begin{align} & \rho_{\beta} \rightharpoonup \rho_0 \mbox{ in } L^{\frac{q}{q-1}}(\Omega), \mbox{ as } \beta \to 0^+ , \end{align}

(4.12)\begin{align} & \rho_{\beta}(x) \to \rho_0(x) \mbox{ a.e. in } \Omega, \mbox{ as}\ \beta \to 0^+ \end{align}

and

(4.13)\begin{equation} 0 \leq \rho_0(x) \leq |u_0(x)|^{q-1} \mbox{ a.e. in } \Omega.\end{equation}

Now, let us deal with the family of vector fields $({\bf z}_\beta )_{0 < \beta < \beta _0}$. Note that, since $\|{\bf z}_\beta \|_\infty \leq 1$ for all $\beta \in (0,\,\beta _0)$, then there exists ${\bf z}_0 \in L^\infty (\Omega,\,\mathbb {R}^N)$, such that

(4.14)\begin{equation} {\bf z}_\beta \overset{\ast}{\rightharpoonup} {\bf z}_0 \quad \mbox{in}\ L^\infty(\Omega,\,\mathbb{R}^N).\end{equation}

This, on the other hand, implies that ${\bf z}_\beta \rightharpoonup {\bf z}_0$ in $L^1(\Omega,\,\mathbb {R}^N)$, i.e., for all $\psi \in L^\infty (\Omega,\,\mathbb {R}^N)$,

(4.15)\begin{equation} \int_\Omega {\bf z}_\beta \cdot \psi \,{\rm d}x \to \int_\Omega {\bf z}_0 \cdot \psi \,{\rm d}x, \quad \mbox{as}\ \beta \to 0^+.\end{equation}

For every $\varphi \in C^\infty _c(\Omega )$, since $\nabla \varphi \in L^\infty (\Omega,\,\mathbb {R}^N)$, by (4.15), we have that

\[ \int_\Omega {\bf z}_\beta\cdot \nabla\phi \,{\rm d}x \to \int_\Omega {\bf z}_0 \cdot \nabla \phi \,{\rm d}x, \quad \mbox{as}\ \beta \to 0^+, \]

from where it follows that

(4.16)\begin{equation} \mbox{div}\, {\bf z}_\beta \to \mbox{div}\, {\bf z}_0, \quad \mbox{in}\ \mathcal{D}'(\Omega).\end{equation}

Hence, from (4.11) and (4.16), we have that

(4.17)\begin{equation} -\mbox{div} \, {\bf z}_0 = \rho_0 \quad \mbox{in}\ \mathcal{D}'(\Omega). \end{equation}

Lemma 4.2 The function $u_0$ and the vector field ${\bf z}_0\!$ satisfy the following equality,

\[ ({\bf z}_0,D u_0) = |D u_0| \quad \mbox{in}\ \mathcal{M}(\Omega). \]

Proof. First of all, note that, from (2.1),

\[ ({\bf z}_0,Du_0) \leq |Du_0| \quad \mbox{in}\ \mathcal{M}(\Omega). \]

For the inverse inequality, let $\varphi \in \mathcal {D}(\Omega )$, $\varphi \geq 0$. In (4.1), let us take $\varphi u_\beta$ as test function in (4.1). Then,

\[ \int_\Omega \varphi ({\bf z}_\beta,Du_\beta) = \int_\Omega \varphi u_\beta \rho_\beta \,{\rm d}x - \int_\Omega u_\beta {\bf z}_\beta\cdot \nabla \varphi \,{\rm d}x. \]

Taking into account that $({\bf z}_\beta,\,Du_\beta ) = |Du_\beta |$ in $\mathcal {M}(\Omega )$,

\[ \int_\Omega \varphi |Du_\beta| = \int_\Omega \varphi u_\beta \rho_\beta \,{\rm d}x - \int_\Omega u_\beta {\bf z}_\beta\cdot \nabla \varphi \,{\rm d}x. \]

Taking the $\liminf$ as $\beta \to 0^+$, from the lower semicontinuity of the norm in $BV(\Omega )$ with respect to the $L^r$ convergence, (4.9), (4.11) and (4.16), it follows that

\begin{align*} \int_\Omega \varphi |Du_0| & \leq \liminf_{\beta \to 0^+} \left(-\int_\Omega \varphi u_\beta \mbox{div}\, {\bf z}_\beta \,{\rm d}x - \int_\Omega u_\beta {\bf z}_\beta\cdot \nabla \varphi \,{\rm d}x\right)\\ & ={-}\int_\Omega \varphi u_0 \mbox{div}\, {\bf z}_0 \,{\rm d}x - \int_\Omega u_0 {\bf z}_0\cdot \nabla \varphi \,{\rm d}x\\ & = \int_\Omega \varphi ({\bf z}_0, Du_0). \end{align*}

This, in turn, proves that $|Du_0| \leq ({\bf z}_0,\,Du_0)$ and this finishes the proof.

Lemma 4.3 The function $u_0$ satisfies $[\textbf {z}_0,\,\nu ] \in \mbox {sign}(-u_0)$ on $\partial \Omega$.

Proof. As in lemma 3.8, it is enough to show that

(4.18)\begin{equation} \int_\Omega (| u_0 | + u_0[\textbf{z}_0,\nu])d\mathcal{H}^{N-1} = 0.\end{equation}

In order to verify (4.18), let us consider $(u_\beta - \varphi ) \in BV(\Omega )\cap L^\infty (\Omega )$ as test function in (4.1), where $\varphi \in \mathcal {D}(\Omega )$. Then, from (2.3) and (4.1), we get

(4.19)\begin{align} \int_\Omega |Du_\beta| + \int_{\partial \Omega} |u_\beta| d\mathcal{H}^{N-1} & = \int_\Omega ({\bf z}_\beta,Du_\beta) - \int_{\partial \Omega} u_\beta [{\bf z}_\beta,\nu] d\mathcal{H}^{N-1}\nonumber\\ & ={-}\int_\Omega u_\beta \mbox{div}\, {\bf z}_\beta\\ & =\int_\Omega \varphi \mbox{div}\, {\bf z}_\beta + \int_\Omega u_\beta \rho_\beta \,{\rm d}x - \int_\Omega \varphi \rho_\beta\nonumber\\ & =\int_\Omega u_\beta \rho_\beta \,{\rm d}x. \nonumber \end{align}

Then, calculating the $\liminf$ in (4.19), from the lower semicontinuity of the norm in $BV(\Omega )$, (4.17) and lemma 4.2, we have that

\begin{align*} \int_\Omega |Du_0| \int_{\partial \Omega}|u_0| d\mathcal{H}^{N-1} & \leq \int_\Omega u_0 \rho_0 \,{\rm d}x\\ & ={-}\int_\Omega u_0 \mbox{div}\, {\bf z}_0 \\ & =\int_\Omega ({\bf z}_0,Du_0) - \int_{\partial \Omega} u_0 [{\bf z}_0,\nu] \mathcal{H}^{N-1} \\ & =\int_\Omega |Du_0| - \int_{\partial \Omega} u_0 [{\bf z}_0,\nu] \mathcal{H}^{N-1}. \end{align*}

From the last inequality, it follows that

\[ | u_0 | + u_0[\textbf{z}_0,\nu] \leq 0 \quad \mathcal{H}^{N-1}-\mbox{a.e. on }\partial \Omega. \]

Since the inverse inequality is trivial, it follows that (4.18) holds.

Then, from (4.17) and lemmas 4.2 and 4.3, it follows that $u_0$ is a solution of (1.4).

Now, in order to end up the proof of theorem 1.2, let us show that there exist constants $\mu,\, \beta _{0} > 0$, such that

(4.20)\begin{equation} |\{x\in \Omega: u_\beta(x)>\beta\}|\geq \mu, \ \mbox{ for all } \ \beta\in(0, \beta_{0}), \end{equation}

From (3.55) it follows that

\[ 0 < \alpha + o_p(1) \leq c_{p,\beta} \leq \frac{1}{p}\int_{\Omega}\rho_{p,\beta} u_{p,\beta} \,{\rm d}x + o_p(1), \]

where $\alpha$ is independent of $\beta$ and $p\in (1,\, \overline {p})$. Since $\rho _{p,\beta }$ verifies (3.3),

(4.21)\begin{equation} \alpha\leq \frac{\beta^{q}}{p}|\Omega|+\frac{1}{p}\int_{\{u_{p,\beta}>\beta\}}u_{p,\beta}^{q} \,{\rm d}x + o_p(1), \end{equation}

for all $\beta >0$ and $p\in (1,\, \overline {p})$. To conclude the proof, it is enough to prove that

(4.22)\begin{equation} \limsup\limits_{p\to 1^+}\int_{\{u_{p,\beta}>\beta\}}u_{p,\beta}^{q} \,{\rm d}x\leq \int_{\{u_\beta\geq \beta\}}u_\beta^{q} \,{\rm d}x. \end{equation}

In fact, if (4.22) holds true, then from (3.26), passing to the upper limit as $p\to 1^+$ in (4.21), we get

(4.23)\begin{equation} \alpha\leq \beta^{q}|\Omega|+\int_{\{u_\beta\geq \beta\}}u_\beta^{q} \,{\rm d}x\leq 2\beta^{q}|\Omega|+\int_{\{u_\beta> \beta\}}u_\beta^{q} \,{\rm d}x, \end{equation}

for all $\beta >0$. Now, suppose by contradiction that there exists a subsequence $\beta _{n}\to 0$ such that

(4.24)\begin{equation} |\{u_\beta>\beta_{n}\}|\to 0, \ \mbox{as} \ \beta_{n}\to 0. \end{equation}

Since, by (4.23), we have

\[ \alpha\leq 2\beta_{n}^{q}|\Omega|+\int_{\Omega}u_\beta^{q}\chi_{\{u_\beta>\beta_{n}\}} \,{\rm d}x, \]

it follows from Hölder's inequality that

(4.25)\begin{equation} \alpha\leq 2\beta_{n}^{q}|\Omega|+\left(\int_{\Omega}u_\beta^{r}\,{\rm d}x\right)^{\frac{q}{r}}|\{u_\beta>\beta_{n}\}|^{\frac{r-q}{r}}, \end{equation}

for some $q< r< N/(N-1)$. Then, (4.24) and (4.25) would lead us to a contradiction.

Hence, to conclude the proof, it remains us to show (4.22). For this purpose, observe that

(4.26)\begin{align} \int_{\{u_{p,\beta}>\beta\}}u_{p,\beta}^{q} \,{\rm d}x & = \int_{\Omega}u_{p,\beta}^{q} \chi_{\{u_{p,\beta}>\beta\}}\,{\rm d}x\nonumber\\ & \leq \int_{\Omega}u_{p,\beta}^{q} \chi_{\{u_{p,\beta}>\beta\}\cap \{u_\beta<\beta\}}\,{\rm d}x+\int_{\Omega}u_{p,\beta}^{q} \chi_{\{u_\beta\geq \beta\}}\,{\rm d}x. \end{align}

Moreover, since

(4.27)\begin{equation} \chi_{\{u_{p,\beta}>\beta\}\cap \{u_\beta<\beta\}}(x)\to 0 \ \mbox{a.e. in}\ \Omega, \ as \ p\to 1^+, \end{equation}

it follows from (3.26), (4.26), (4.27) and Lebesgue's dominated convergence theorem, that (4.22) holds true.

To conclude that $u_0$ is nontrivial, note that by (4.23), $u_0\geq 0$ and Lebesgue's dominated convergence theorem,

\[ 0<\alpha\leq \int_{\Omega}u_0^{q}, \]

then, $u_0\not \equiv 0.$ Finally, since $\rho _\beta (x)\in [\underline {f}_\beta (u_\beta (x)),\,\overline {f}_\beta (u_\beta (x))],$ by (3.5), (4.9) and (4.12), we conclude that $\rho _0(x)=u_0(x)^{q-1}$ a.e. in $\Omega$ and therefore $u_0$ is solution of the continuous problem (1.4).