Published online by Cambridge University Press: 26 May 2009
Let a, c ≥ 0 and let B be a compact set of scalars. We show that if X is a Banach space such that the canonical projection π from X*** onto X* satisfies the inequality
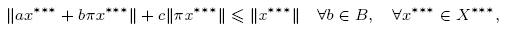
and 1 ≤ λ < max |B| + c, then every λ-commuting bounded compact approximation of the identity of X is shrinking. This generalizes a theorem by Godefroy and Saphar from 1988. As an application, we show that under the conditions described above both X and X* have the metric compact approximation property (MCAP). Relying on the Willis construction, we show that the commuting MCAP does not imply the approximation property.