Published online by Cambridge University Press: 18 January 2019
In this paper, we study negative classical solutions and stable solutions of the following k-Hessian equation
with radial structure, where n ⩾ 3, 1 < k < n/2 and p > 1. This equation is related to the extremal functions of the Hessian Sobolev inequality on the whole space. Several critical exponents including the Serrin type, the Sobolev type, and the Joseph-Lundgren type, play key roles in studying existence and decay rates. We believe that these critical exponents still come into play to research k-Hessian equations without radial structure.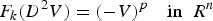 $$F_k(D^2V) = (-V)^p\quad {\rm in}\;\; R^n$$
$$F_k(D^2V) = (-V)^p\quad {\rm in}\;\; R^n$$