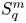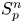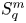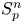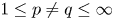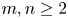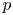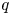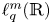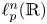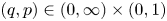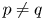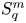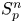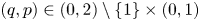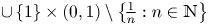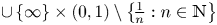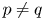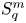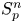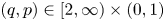1. Introduction and main results
In a recent article [Reference Chattopadhyay, Hong, Pal, Pradhan and Ray6], the authors have studied isometric embeddability of $S_q^m$![]() into $S_p^n$
into $S_p^n$![]() for $1\leq p\neq q\leq \infty$
for $1\leq p\neq q\leq \infty$![]() and $m,n\geq 2.$
and $m,n\geq 2.$![]() This partially established non-commutative analogues of the results appearing in [Reference Lyubich26–Reference Lyubich and Vaserstein30]. The motivation behind this study was two-fold. Firstly, the study of isometric embeddability for commutative $L_p$
This partially established non-commutative analogues of the results appearing in [Reference Lyubich26–Reference Lyubich and Vaserstein30]. The motivation behind this study was two-fold. Firstly, the study of isometric embeddability for commutative $L_p$![]() -spaces is an exciting topic of research. This began from the seminal paper of Banach [Reference Banach3] and continued by several authors. We refer to [Reference Delbaen, Jarchow and Pełczyński7–Reference Fleming and Jamison9] and references therein for a comprehensive study. We also point out [Reference Herz12, Reference Koldobsky and König22, Reference Lev́y25, Reference Rosenthal41, Reference Schoenberg42] for exciting connections with various other fields of mathematics, for example, probability theory and combinatorics. Motivated by quantum mechanics, non-commutative analysis has made great advancements in the past few decades. The theory of non-commutative $L_p$
-spaces is an exciting topic of research. This began from the seminal paper of Banach [Reference Banach3] and continued by several authors. We refer to [Reference Delbaen, Jarchow and Pełczyński7–Reference Fleming and Jamison9] and references therein for a comprehensive study. We also point out [Reference Herz12, Reference Koldobsky and König22, Reference Lev́y25, Reference Rosenthal41, Reference Schoenberg42] for exciting connections with various other fields of mathematics, for example, probability theory and combinatorics. Motivated by quantum mechanics, non-commutative analysis has made great advancements in the past few decades. The theory of non-commutative $L_p$![]() -spaces is an outgrowth of this direction of research. In [Reference Arazy1, Reference Junge, Ruan and Sherman19, Reference Yeadon46], the authors have studied isometries on non-commutative $L_p$
-spaces is an outgrowth of this direction of research. In [Reference Arazy1, Reference Junge, Ruan and Sherman19, Reference Yeadon46], the authors have studied isometries on non-commutative $L_p$![]() -spaces and established non-commutative analogues of results of Banach [Reference Banach3] and Lamperti [Reference Lamperti24]. A remarkable progress took place after the successful development of operator space theory and non-commutative probability theory. We refer to [Reference Junge13, Reference Junge14, Reference Junge and Parcet18, Reference Pisier32, Reference Xu45]. We also refer to [Reference Haagerup, Rosenthal and Sukochev11, Reference Junge, Nielsen, Ruan and Xu15–Reference Junge, Sukochev and Zanin20, Reference Raynaud and Xu38, Reference Sukochev and Xu44] and references therein for more information in this direction of research. Therefore, in view of the results appearing in [Reference Lyubich26–Reference Lyubich and Vaserstein30], it is natural to study non-commutative analogues of them in the context of non-commutative isometric or isomorphic embedding theory. The second motivation behind [Reference Chattopadhyay, Hong, Pal, Pradhan and Ray6] was again operator space theory and its connections to boundary normal dilation, where such non-commutative isometric embeddability was crucial. This was also motivated from a guess of Pisier and Misra. We refer to [Reference Ray37] for more on this (see also [Reference Gupta and Reza10]).
-spaces and established non-commutative analogues of results of Banach [Reference Banach3] and Lamperti [Reference Lamperti24]. A remarkable progress took place after the successful development of operator space theory and non-commutative probability theory. We refer to [Reference Junge13, Reference Junge14, Reference Junge and Parcet18, Reference Pisier32, Reference Xu45]. We also refer to [Reference Haagerup, Rosenthal and Sukochev11, Reference Junge, Nielsen, Ruan and Xu15–Reference Junge, Sukochev and Zanin20, Reference Raynaud and Xu38, Reference Sukochev and Xu44] and references therein for more information in this direction of research. Therefore, in view of the results appearing in [Reference Lyubich26–Reference Lyubich and Vaserstein30], it is natural to study non-commutative analogues of them in the context of non-commutative isometric or isomorphic embedding theory. The second motivation behind [Reference Chattopadhyay, Hong, Pal, Pradhan and Ray6] was again operator space theory and its connections to boundary normal dilation, where such non-commutative isometric embeddability was crucial. This was also motivated from a guess of Pisier and Misra. We refer to [Reference Ray37] for more on this (see also [Reference Gupta and Reza10]).
Beyond the range of $(p,q)\in [1,\infty ]\times [1,\infty ],$![]() some results are also known. By [Reference Junge13] for all $0< p< q<2,$
some results are also known. By [Reference Junge13] for all $0< p< q<2,$![]() $L_q(\mathcal {R}\overline {\otimes }B(\ell _2))$
$L_q(\mathcal {R}\overline {\otimes }B(\ell _2))$![]() and hence $L_q(\mathcal {R})$
and hence $L_q(\mathcal {R})$![]() embeds isometrically into $L_p(\mathcal {R})$
embeds isometrically into $L_p(\mathcal {R})$![]() where $\mathcal {R}$
where $\mathcal {R}$![]() is a hyperfinite type $\text {II}_1$
is a hyperfinite type $\text {II}_1$![]() factor. This generalized remarkable results due to [Reference Bretagnolle, Dacunha-Castelle and Krivine5] in the non-commutative setting. In [Reference Sukochev and Xu44], Sukochev and Xu studied when $L_p(\mathcal {N})$
factor. This generalized remarkable results due to [Reference Bretagnolle, Dacunha-Castelle and Krivine5] in the non-commutative setting. In [Reference Sukochev and Xu44], Sukochev and Xu studied when $L_p(\mathcal {N})$![]() embeds into $L_p(\mathcal {M})$
embeds into $L_p(\mathcal {M})$![]() for $0< p<1,$
for $0< p<1,$![]() where $\mathcal {M}$
where $\mathcal {M}$![]() and $\mathcal {N}$
and $\mathcal {N}$![]() are semifinite von Neumann algebras. We also refer [Reference Randrianantoanina36, Reference Raynaud and Xu38] for related work. Despite these remarkable developments, the case when $S_q^m$
are semifinite von Neumann algebras. We also refer [Reference Randrianantoanina36, Reference Raynaud and Xu38] for related work. Despite these remarkable developments, the case when $S_q^m$![]() embeds isometrically into $S_p^n$
embeds isometrically into $S_p^n$![]() is not well studied for $0< p\neq q\leq \infty$
is not well studied for $0< p\neq q\leq \infty$![]() . The question when $S_q^m$
. The question when $S_q^m$![]() embeds isometrically into $S_p^n$
embeds isometrically into $S_p^n$![]() for $0< p\neq q\leq \infty$
for $0< p\neq q\leq \infty$![]() was asked by Xu to the authors.
was asked by Xu to the authors.
Question 1.1 Let $0< p\neq q\leq \infty$![]() and $m,n\geq 2.$
and $m,n\geq 2.$![]() When does $S_q^m$
When does $S_q^m$![]() embeds isometrically into $S_p^n$
embeds isometrically into $S_p^n$![]() ?
?
Note that [Reference Chattopadhyay, Hong, Pal, Pradhan and Ray6, Reference Ray37] give partial answers to question 1.1 when $1\leq p\neq q\leq \infty.$![]() The main novelty of our work in this article is to study isometric embeddability of $S_q^m$
The main novelty of our work in this article is to study isometric embeddability of $S_q^m$![]() into $S_p^n$
into $S_p^n$![]() where $0< p\neq q\leq \infty$
where $0< p\neq q\leq \infty$![]() as non-commutative quasi-Banach spaces which goes beyond the foregoing range of $p$
as non-commutative quasi-Banach spaces which goes beyond the foregoing range of $p$![]() and $q$
and $q$![]() . We also study the classical case, i.e. when $\ell _q^m$
. We also study the classical case, i.e. when $\ell _q^m$![]() embeds isometrically into $\ell _p^n$
embeds isometrically into $\ell _p^n$![]() for $m,n\geq 2$
for $m,n\geq 2$![]() and $0< p\neq q\leq \infty.$
and $0< p\neq q\leq \infty.$![]() Note that the case when $1\leq p\neq q\leq \infty$
Note that the case when $1\leq p\neq q\leq \infty$![]() has been extensively studied in [Reference Lyubich26–Reference Lyubich and Vaserstein30]. However, the authors did not consider the cases when $p$
has been extensively studied in [Reference Lyubich26–Reference Lyubich and Vaserstein30]. However, the authors did not consider the cases when $p$![]() and $q$
and $q$![]() are allowed to be strictly less than $1$
are allowed to be strictly less than $1$![]() and to our surprise there is no more study in the literature on this. Thus, our study is new even in the commutative case. Our first theorem is the following.
and to our surprise there is no more study in the literature on this. Thus, our study is new even in the commutative case. Our first theorem is the following.
Theorem 1.2 (Isometric embeddability between commutative quasi-Banach spaces $\ell _p^n(\mathbb {K})$ )
)
Let $(q,p)\in (0,\infty )\times (0,1)$![]() , and $2\leq m\leq n<\infty$
, and $2\leq m\leq n<\infty$![]() and $p\neq q$
and $p\neq q$![]() . Then, there is no isometric embedding of $\ell _q^m(\mathbb {K})$
. Then, there is no isometric embedding of $\ell _q^m(\mathbb {K})$![]() into $\ell _p^n(\mathbb {K})$
into $\ell _p^n(\mathbb {K})$![]() for each of the following cases$:$
for each of the following cases$:$![]()
(1) $\mathbb {K}=\mathbb {C}$
 and $q\in (0,\infty )\setminus 2\mathbb {N}$
and $q\in (0,\infty )\setminus 2\mathbb {N}$ .
.(2) $\mathbb {K}=\mathbb {R}$
 .
.
In the above theorem, the results for real and complex cases are different. The technical reason behind this is that if we consider the complex field instead of $\mathbb {R}$![]() , that is $\ell _q^m(\mathbb {C})$
, that is $\ell _q^m(\mathbb {C})$![]() , then in the proof of theorem 1.2, it may happen that $\left.\frac {{\rm d}^2}{{\rm d}t^2}\right |_{t=0}{\lVert }{\boldsymbol {a}\!+\!t\boldsymbol {b}}{\rVert }_p^p\!=\!0$
, then in the proof of theorem 1.2, it may happen that $\left.\frac {{\rm d}^2}{{\rm d}t^2}\right |_{t=0}{\lVert }{\boldsymbol {a}\!+\!t\boldsymbol {b}}{\rVert }_p^p\!=\!0$![]() , where $\|\boldsymbol {a}\|_p=\|\boldsymbol {b}\|_p=1$
, where $\|\boldsymbol {a}\|_p=\|\boldsymbol {b}\|_p=1$![]() and in that case we can't conclude anything. Please see remark 3.1 for more details on this. These kinds of facts are one of the many subtleties in our work.
and in that case we can't conclude anything. Please see remark 3.1 for more details on this. These kinds of facts are one of the many subtleties in our work.
Theorem 1.3 (Isometric embeddability between non-commutative quasi-Banach spaces $S_p^n$ )
)
Let $p\in (0,1)$![]() , and $2\leq m\leq n$
, and $2\leq m\leq n$![]() .
.
(1) There is no isometric embedding of $S_q^m$
 into $S_p^n$
into $S_p^n$ for $q\in (0,2)\setminus \{1\}$
for $q\in (0,2)\setminus \{1\}$ and $p\neq q$
and $p\neq q$ .
.(2) Let $2\leq q< \infty.$
 Then, there is no isometric embedding $T:S_q^m\to S_p^n$
Then, there is no isometric embedding $T:S_q^m\to S_p^n$ with
with$T(\text {diag}(1,0,\ldots,0))=A,$
 and $T(\text {diag}(0,1,\ldots,0))=B$
and $T(\text {diag}(0,1,\ldots,0))=B$ such that
such that
• $A,B\in M_n^{sa},$

• either $A\geq 0$
 or $A\leq 0$
or $A\leq 0$ .
.
(3) There is no isometric embedding of $S_1^m$
 into $S_p^n$
into $S_p^n$ for $p\in (0,1)\setminus \{\frac {1}{k}:k\in \mathbb {N}\}$
for $p\in (0,1)\setminus \{\frac {1}{k}:k\in \mathbb {N}\}$ .
.(4) There is no isometric embedding of $S_\infty ^m$
 into $S_p^n$
into $S_p^n$ for $p\in (0,1)\setminus \{\frac {1}{k}:k\in \mathbb {N}\}$
for $p\in (0,1)\setminus \{\frac {1}{k}:k\in \mathbb {N}\}$ .
.
We refer to § 2 for unexplained notations in the above theorems. Note that theorem 1.3 together with results from [Reference Chattopadhyay, Hong, Pal, Pradhan and Ray6, Reference Ray37] give an answer to question 1.1 for a wide range of $p$![]() and $q.$
and $q.$![]() It is interesting to observe that in view of [Reference Junge13], theorem 1.3 indicates sharp contrast between finite dimensional and infinite dimensional cases and shows that isometric embeddability problem between non-commutative Lp-spaces also depends on the type of the underlying von Neumann algebras. Each part of theorem 1.3 has been proven using different methods and each of them requires specific techniques developed before that. For these reasons, we have proved them separately in theorems 4.8, 4.9, 4.10, 4.11 and 4.13.
It is interesting to observe that in view of [Reference Junge13], theorem 1.3 indicates sharp contrast between finite dimensional and infinite dimensional cases and shows that isometric embeddability problem between non-commutative Lp-spaces also depends on the type of the underlying von Neumann algebras. Each part of theorem 1.3 has been proven using different methods and each of them requires specific techniques developed before that. For these reasons, we have proved them separately in theorems 4.8, 4.9, 4.10, 4.11 and 4.13.
The paper is organized as the following. In § 2, we recall necessary background and prove some useful results. In § 3, we study the isometric embeddability of $\ell _q^m$![]() into $\ell _p^n$
into $\ell _p^n$![]() as commutative quasi-Banach spaces. In § 4, we recall and prove many facts about operator derivatives and study the isometric embeddability of $S_q^m$
as commutative quasi-Banach spaces. In § 4, we recall and prove many facts about operator derivatives and study the isometric embeddability of $S_q^m$![]() into $S_p^n$
into $S_p^n$![]() as non-commutative quasi-Banach spaces.
as non-commutative quasi-Banach spaces.
2. Preliminaries
We let $\mathbb {K}$![]() denote the scalar field. That is $\mathbb {K}=\mathbb {R}$
denote the scalar field. That is $\mathbb {K}=\mathbb {R}$![]() or $\mathbb {C}$
or $\mathbb {C}$![]() . For $0< p<\infty$
. For $0< p<\infty$![]() , we denote by $\ell _p^n(\mathbb {K})$
, we denote by $\ell _p^n(\mathbb {K})$![]() the $\mathbb {K}$
the $\mathbb {K}$![]() -linear space $\mathbb {K}^n$
-linear space $\mathbb {K}^n$![]() equipped with the $\ell _p$
equipped with the $\ell _p$![]() semi-norm
semi-norm

For simplicity, we write $\ell _p^n(\mathbb {C})=\ell _p^n$![]() . Let $\mathcal {M}$
. Let $\mathcal {M}$![]() be a von Neumann algebra with a normal semifinite faithful trace $\tau$
be a von Neumann algebra with a normal semifinite faithful trace $\tau$![]() . Let $\mathcal {S}(\mathcal {M})$
. Let $\mathcal {S}(\mathcal {M})$![]() be the linear span of positive elements with finite support. Let $0< p<\infty.$
be the linear span of positive elements with finite support. Let $0< p<\infty.$![]() For $x\in \mathcal {S}(\mathcal {M}),$
For $x\in \mathcal {S}(\mathcal {M}),$![]() define $\|x\|_p:=(\tau (|x|^p))^{\frac {1}{p}}$
define $\|x\|_p:=(\tau (|x|^p))^{\frac {1}{p}}$![]() . For $p\geq 1,$
. For $p\geq 1,$![]() $\mathcal {S}(\mathcal {M})$
$\mathcal {S}(\mathcal {M})$![]() is a normed space and for $0< p<1,$
is a normed space and for $0< p<1,$![]() it is a quasi-normed space. Then, $L_p(\mathcal {M})$
it is a quasi-normed space. Then, $L_p(\mathcal {M})$![]() is defined to be $\overline {(\mathcal {S}(\mathcal {M}),\|.\|_p)}$
is defined to be $\overline {(\mathcal {S}(\mathcal {M}),\|.\|_p)}$![]() with respect to the metric $d_p(x,y):=\|x-y\|_p^p$
with respect to the metric $d_p(x,y):=\|x-y\|_p^p$![]() . One denotes $L_\infty (\mathcal {M})=\mathcal {M}$
. One denotes $L_\infty (\mathcal {M})=\mathcal {M}$![]() . Thus, for $1\leq p\leq \infty,$
. Thus, for $1\leq p\leq \infty,$![]() $L_p(\mathcal {M})$
$L_p(\mathcal {M})$![]() is a Banach space and for $0< p<1,$
is a Banach space and for $0< p<1,$![]() it becomes a quasi-Banach space. When $\mathcal {M}=\mathcal {B}(\ell _2^n)$
it becomes a quasi-Banach space. When $\mathcal {M}=\mathcal {B}(\ell _2^n)$![]() with the usual trace $Tr,$
with the usual trace $Tr,$![]() the corresponding non-commutative $L_p$
the corresponding non-commutative $L_p$![]() -space is called the Schatten $p$
-space is called the Schatten $p$![]() -class and denoted by $S_p^n$
-class and denoted by $S_p^n$![]() . The set of all $n\times n$
. The set of all $n\times n$![]() complex matrices is denoted by $M_n$
complex matrices is denoted by $M_n$![]() . We denote $M_n^{sa}$
. We denote $M_n^{sa}$![]() to be the set of all $n\times n$
to be the set of all $n\times n$![]() self-adjoint matrices. For $0< p<1$
self-adjoint matrices. For $0< p<1$![]() , it is well known that $\|.\|_{L_p(\mathcal {M})}$
, it is well known that $\|.\|_{L_p(\mathcal {M})}$![]() satisfies
satisfies
(1) $\|A+B\|_p\leq 2^{\frac {1}{p}-1} (\|A\|_p+\|B\|_p ),\quad \forall \, A,\,B\in L_p(\mathcal {M}),$

(2) $\|UAV\|_p=\|A\|_p$
 for all unitary operators $U, V$
for all unitary operators $U, V$ in $\mathcal {M}$
in $\mathcal {M}$ , and $A\in L_p(\mathcal {M})$
, and $A\in L_p(\mathcal {M})$ , that is $\|\cdot \|_p$
, that is $\|\cdot \|_p$ is a unitary invariant quasi-norm.
is a unitary invariant quasi-norm.
It is natural to ask that which class of operators in $S_p^n$![]() satisfies the triangular inequality (i.e. $\|A+B\|_p\leq \|A\|_p+\|B\|_p$
satisfies the triangular inequality (i.e. $\|A+B\|_p\leq \|A\|_p+\|B\|_p$![]() ). The problem of the isometric embeddability of $S_q^m$
). The problem of the isometric embeddability of $S_q^m$![]() into $S_p^n$
into $S_p^n$![]() for $1\leq q\leq \infty$
for $1\leq q\leq \infty$![]() can possibly shed some light on this question. We now recall a few useful tools.
can possibly shed some light on this question. We now recall a few useful tools.
2.1. Non-commutative Clarkson's inequality for Schatten class operators
A new tool in our work is the non-commutative Clarkson's inequality. This helps us to obtain the crucial lemma 2.2. However, we want to emphasize that non-commutative Clarkson's inequality alone cannot solve our problem as we know that non-commutative Clarkson's inequality is also true for general non-commutative $L_p$![]() -spaces but the existence of isometric embeddability between non-commutative $L_p$
-spaces but the existence of isometric embeddability between non-commutative $L_p$![]() -spaces are completely different if the underlying von Neumann algebras are of different type as we have pointed out before. We refer [Reference McCarthy31] for the following inequality.
-spaces are completely different if the underlying von Neumann algebras are of different type as we have pointed out before. We refer [Reference McCarthy31] for the following inequality.
Theorem 2.1 Let $A,B\in S_p^n$![]() . Then, for $0\leq p\leq 2$
. Then, for $0\leq p\leq 2$![]() , $A, B$
, $A, B$![]() satisfies
satisfies
and for $2\leq p<\infty$![]() ,
,
Observe that, for $0< q<\infty$![]() , $0< p< \infty$
, $0< p< \infty$![]() , $2\leq m\leq n<\infty$
, $2\leq m\leq n<\infty$![]() , isometric embeddability of $S_q^m$
, isometric embeddability of $S_q^m$![]() into $S_p^n$
into $S_p^n$![]() implies existence of a linear isometry $T:\ell _q^2(\mathbb {C})\to S_p^n$
implies existence of a linear isometry $T:\ell _q^2(\mathbb {C})\to S_p^n$![]() , which further implies the following equality
, which further implies the following equality
Now if we assume that for $0< q<\infty,~ 0< p\leq 2$![]() , $S_q^m$
, $S_q^m$![]() isometrically embeds into $S_p^n$
isometrically embeds into $S_p^n$![]() , then non-commutative Clarkson's inequality (2.1) and the above identity (2.3) together imply
, then non-commutative Clarkson's inequality (2.1) and the above identity (2.3) together imply
In (2.4), the last inequality implies that $p\leq q$![]() . On the other hand if we assume that for $0< q<\infty, 2< p< \infty$
. On the other hand if we assume that for $0< q<\infty, 2< p< \infty$![]() , $S_q^m$
, $S_q^m$![]() isometrically embeds into $S_p^n$
isometrically embeds into $S_p^n$![]() , then non-commutative Clarkson's inequality (2.1) and the above identity (2.3) together implies
, then non-commutative Clarkson's inequality (2.1) and the above identity (2.3) together implies
Therefore, in this case, $p\geq q$![]() is necessary for isometric embeddability of $S_q^m$
is necessary for isometric embeddability of $S_q^m$![]() into $S_p^n$
into $S_p^n$![]() . But, in both cases, non-commutative Clarkson's inequality does not give anything more to these embedding problems. In the following lemma, we summarize the above discussions.
. But, in both cases, non-commutative Clarkson's inequality does not give anything more to these embedding problems. In the following lemma, we summarize the above discussions.
Lemma 2.2 Let $2\leq m\leq n<\infty,\, 0< p\neq q<\infty$![]() . Suppose $S_q^m$
. Suppose $S_q^m$![]() isometrically embeds into $S_p^n$
isometrically embeds into $S_p^n$![]() .
.
(1) If $0< q<\infty$
 , $0< p\leq 2$
, $0< p\leq 2$ , then $p< q$
, then $p< q$ .
.(2) If $0< q<\infty$
 , $2\leq p<\infty$
, $2\leq p<\infty$ , then $p>q$
, then $p>q$ .
.
Remark 2.3 Let $\mathcal {M}$![]() be the hyperfinite type $II_1$
be the hyperfinite type $II_1$![]() factor. Note that as in lemma 2.2, one can easily see that if $0< q<\infty$
factor. Note that as in lemma 2.2, one can easily see that if $0< q<\infty$![]() and $0< p\leq 2$
and $0< p\leq 2$![]() , then $L_q(\mathcal {M})$
, then $L_q(\mathcal {M})$![]() cannot embed isometrically into $L_p(\mathcal {M})$
cannot embed isometrically into $L_p(\mathcal {M})$![]() whenever $p>q.$
whenever $p>q.$![]() Also for $0< q<\infty$
Also for $0< q<\infty$![]() and $2\leq p<\infty,$
and $2\leq p<\infty,$![]() $L_q(\mathcal {M})$
$L_q(\mathcal {M})$![]() cannot embed isometrically into $L_p(\mathcal {M})$
cannot embed isometrically into $L_p(\mathcal {M})$![]() if $p< q.$
if $p< q.$![]()
To continue the study of the isometric embedding problem, here we need to introduce two more novel ingredients, which were also crucial in our previous study [Reference Chattopadhyay, Hong, Pal, Pradhan and Ray6], namely the Kato–Rellich theorem and multiple operator integrals in perturbation theory.
2.2. A simple version of Kato–Rellich theorem
Theorem 2.4 $($![]() see [Reference Rellich39, page 31, chapter I], [Reference Baumgärtel4, P. 21, theorem 1]$)$
see [Reference Rellich39, page 31, chapter I], [Reference Baumgärtel4, P. 21, theorem 1]$)$![]() Let $A,B\in M_n^{sa}.$
Let $A,B\in M_n^{sa}.$![]() Then, for all $t_0\in \mathbb {R}$
Then, for all $t_0\in \mathbb {R}$![]() , there exists $\epsilon (t_0)>0$
, there exists $\epsilon (t_0)>0$![]() and real-analytic functions $\lambda _k:(t_0-\epsilon (t_0),t_0+\epsilon (t_0)) \to \mathbb {R},$
and real-analytic functions $\lambda _k:(t_0-\epsilon (t_0),t_0+\epsilon (t_0)) \to \mathbb {R},$![]() where $1\leq k\leq n$
where $1\leq k\leq n$![]() and real-analytic functions $u_{ij}:(t_0-\epsilon (t_0),t_0+\epsilon (t_0)) \to \mathbb {R},$
and real-analytic functions $u_{ij}:(t_0-\epsilon (t_0),t_0+\epsilon (t_0)) \to \mathbb {R},$![]() where $1\leq i,j\leq n$
where $1\leq i,j\leq n$![]() such that
such that
(i) for all $t\in (t_0-\epsilon (t_0),t_0+\epsilon (t_0))$
 , $\{\lambda _1(t),\dots,\lambda _n(t)\}$
, $\{\lambda _1(t),\dots,\lambda _n(t)\}$ is the complete set of eigenvalues of $A+tB$
is the complete set of eigenvalues of $A+tB$ counting multiplicity;
counting multiplicity;(ii) for all $t\in (t_0-\epsilon (t_0),t_0+\epsilon (t_0))$
 , $U(t):=(u_{ij}(t))_{i,j=1}^n$
, $U(t):=(u_{ij}(t))_{i,j=1}^n$ is a unitary matrix;
is a unitary matrix;(iii) for all $t\in (t_0-\epsilon (t_0),t_0+\epsilon (t_0))$
 , $U(t)^*(A+tB)U(t)=\text {diag}(\lambda _1(t),\dots,\lambda _n(t)).$
, $U(t)^*(A+tB)U(t)=\text {diag}(\lambda _1(t),\dots,\lambda _n(t)).$
The above theorem has been studied extensively. We refer [Reference Baumgärtel4, Reference Kato21, Reference Rellich39] for more on related results on this topic.
2.3. Some differentiability criterion
We state and prove the following lemma which will be used later. For any $x\in \mathbb {R},$![]() denote $[x]$
denote $[x]$![]() to be the greatest integer such that $[x]\leq x<[x]+1.$
to be the greatest integer such that $[x]\leq x<[x]+1.$![]() In the following lemma, we say a function is zero time differentiable if and only if it is not differentiable at all.
In the following lemma, we say a function is zero time differentiable if and only if it is not differentiable at all.
Lemma 2.5 Let $p,q$![]() be two positive real numbers and let $f(t)=(1+|t|^q)^p,\, t\in \mathbb {R}$
be two positive real numbers and let $f(t)=(1+|t|^q)^p,\, t\in \mathbb {R}$![]() . Then, at $0$
. Then, at $0$![]() , $f$
, $f$![]() is infinitely many times differentiable if $q\in 2\mathbb {N}$
is infinitely many times differentiable if $q\in 2\mathbb {N}$![]() , $q -1$
, $q -1$![]() times differentiable if $q\in 2\mathbb {N}-1$
times differentiable if $q\in 2\mathbb {N}-1$![]() , and $[\,q\,]$
, and $[\,q\,]$![]() times differentiable if $q\in (0,\infty )\setminus \mathbb {N}$
times differentiable if $q\in (0,\infty )\setminus \mathbb {N}$![]() . Moreover, for any two distinct real numbers $q_1,q_2\in (0,1]$
. Moreover, for any two distinct real numbers $q_1,q_2\in (0,1]$![]() , $(1+|t|^{q_1})^p-a|t|^{q_2}$
, $(1+|t|^{q_1})^p-a|t|^{q_2}$![]() is not differentiable at $0$
is not differentiable at $0$![]() , where $a$
, where $a$![]() is any real constant.
is any real constant.
Proof. The proof of the first part may be safely left to the reader. For the second part, the binomial series expansion of $(1+|t|^{q_1})^p$![]() in a small neighbourhood $\Omega$
in a small neighbourhood $\Omega$![]() of $0$
of $0$![]() is given by
is given by

Let $\boldsymbol {m}$![]() be the least positive integer such that $\boldsymbol mq_1> 1$
be the least positive integer such that $\boldsymbol mq_1> 1$![]() . Since the series in (2.6) is absolutely convergent in $\Omega$
. Since the series in (2.6) is absolutely convergent in $\Omega$![]() , we may write
, we may write

Therefore,

Note that $\left \{\sum \limits _{k=0}^{\boldsymbol {m}-1} (\begin {matrix} p\\ k \end {matrix})|t|^{kq_1}-a|t|^{q_2}\right \}$![]() is not differentiable at $0$
is not differentiable at $0$![]() but $\mathcal {O}(|t|^{\boldsymbol mq_1})$
but $\mathcal {O}(|t|^{\boldsymbol mq_1})$![]() is differentiable at $0$
is differentiable at $0$![]() . Hence, from (2.7), we conclude that $(1+|t|^{q_1})^p-a|t|^{q_2}$
. Hence, from (2.7), we conclude that $(1+|t|^{q_1})^p-a|t|^{q_2}$![]() is not differentiable. This completes the proof of the lemma.
is not differentiable. This completes the proof of the lemma.
3. Isometric embeddability $\ell _q^m(\mathbb {K})\to \ell _p^n(\mathbb {K})$ as commutative quasi-Banach space
as commutative quasi-Banach space
In this section, we study when $\ell _q^m(\mathbb {K})$![]() embeds isometrically into $\ell _p^n(\mathbb {K})$
embeds isometrically into $\ell _p^n(\mathbb {K})$![]() as quasi-Banach spaces.
as quasi-Banach spaces.
Proof of theorem 1.2. On the contrary, suppose there exists an isometric embedding of $\ell _q^m(\mathbb {K})$![]() into $\ell _p^n(\mathbb {K})$
into $\ell _p^n(\mathbb {K})$![]() . Note that as $\ell _q^2(\mathbb {K})$
. Note that as $\ell _q^2(\mathbb {K})$![]() is isometrically embedded into $\ell _q^m(\mathbb {K})$
is isometrically embedded into $\ell _q^m(\mathbb {K})$![]() , $\ell _q^2(\mathbb {K})$
, $\ell _q^2(\mathbb {K})$![]() is also isometrically embedded into $\ell _p^n(\mathbb {K})$
is also isometrically embedded into $\ell _p^n(\mathbb {K})$![]() . Let $T:\ell _q^2(\mathbb {K})\to \ell _p^n(\mathbb {K})$
. Let $T:\ell _q^2(\mathbb {K})\to \ell _p^n(\mathbb {K})$![]() be the linear map that embeds $\ell _q^2(\mathbb {K})$
be the linear map that embeds $\ell _q^2(\mathbb {K})$![]() into $\ell _p^n(\mathbb {K})$
into $\ell _p^n(\mathbb {K})$![]() isometrically. Let $T(1,0)=\boldsymbol {a}:=(a_1,a_2,\ldots,a_n)$
isometrically. Let $T(1,0)=\boldsymbol {a}:=(a_1,a_2,\ldots,a_n)$![]() and $T(0,1)=\boldsymbol {b}:=(b_1,b_2,\dots,b_n)$
and $T(0,1)=\boldsymbol {b}:=(b_1,b_2,\dots,b_n)$![]() . Since $T$
. Since $T$![]() is an isometry, we have
is an isometry, we have


Let $\boldsymbol {m}$![]() be the least positive integer such that ${\boldsymbol m}q> 1$
be the least positive integer such that ${\boldsymbol m}q> 1$![]() . If all $a_k, 1\leq k\leq n$
. If all $a_k, 1\leq k\leq n$![]() are non-zero, then the right-hand side of (3.2) is real-analytic in a small neighbourhood $\Omega \subset \mathbb {R}$
are non-zero, then the right-hand side of (3.2) is real-analytic in a small neighbourhood $\Omega \subset \mathbb {R}$![]() of $0$
of $0$![]() , so the left-hand side of (3.2) is also real-analytic in $\Omega$
, so the left-hand side of (3.2) is also real-analytic in $\Omega$![]() . Therefore, by lemma 2.5, from (3.2) we conclude $q\in 2\mathbb {N}$
. Therefore, by lemma 2.5, from (3.2) we conclude $q\in 2\mathbb {N}$![]() . So when $q\in (0,\infty )\setminus 2\mathbb {N}$
. So when $q\in (0,\infty )\setminus 2\mathbb {N}$![]() , then this situation never exists. Hence, assume $q\in 2 \mathbb {N}$
, then this situation never exists. Hence, assume $q\in 2 \mathbb {N}$![]() and let $\mathbb {K}=\mathbb {R}$
and let $\mathbb {K}=\mathbb {R}$![]() . Then, from (3.1) and (3.2), we have
. Then, from (3.1) and (3.2), we have

Consequently,
Since $1=\|\boldsymbol {a}\|_p^p\leq \|\boldsymbol {a}+t\boldsymbol {b}\|_p^p$![]() , the function $t\mapsto \|\boldsymbol {a}+t\boldsymbol {b}\|_p^p$
, the function $t\mapsto \|\boldsymbol {a}+t\boldsymbol {b}\|_p^p$![]() attains its minimum value at $t=0$
attains its minimum value at $t=0$![]() . Hence, we must have $\dfrac {{\rm d}}{{\rm d}t}\Big |_{t=0}\|\boldsymbol {a}+t\boldsymbol {b}\|_p^p=0$
. Hence, we must have $\dfrac {{\rm d}}{{\rm d}t}\Big |_{t=0}\|\boldsymbol {a}+t\boldsymbol {b}\|_p^p=0$![]() . Therefore, from (3.4), we have
. Therefore, from (3.4), we have
Taking limit $t\to 0$![]() on both sides of (3.5) we have
on both sides of (3.5) we have

which is not possible as $\frac {p}{q}>0$![]() . By similar argument, from (3.3), one can conclude that not all $b_k, 1\leq k\leq n$
. By similar argument, from (3.3), one can conclude that not all $b_k, 1\leq k\leq n$![]() are zero. Therefore, for the scalar field $\mathbb {K}=\mathbb {R}$
are zero. Therefore, for the scalar field $\mathbb {K}=\mathbb {R}$![]() and $q\in (0,\infty )$
and $q\in (0,\infty )$![]() or $\mathbb {K}=\mathbb {C}$
or $\mathbb {K}=\mathbb {C}$![]() and $q\in (0,\infty )\setminus 2\mathbb {N}$
and $q\in (0,\infty )\setminus 2\mathbb {N}$![]() , without loss of generality, we may assume that $a_1=\cdots =a_l=0$
, without loss of generality, we may assume that $a_1=\cdots =a_l=0$![]() for some $l\in \{1,2,\ldots, n-1\}$
for some $l\in \{1,2,\ldots, n-1\}$![]() and $a_k\neq 0$
and $a_k\neq 0$![]() for $l+1\leq k\leq n.$
for $l+1\leq k\leq n.$![]() Now if $b_k=0$
Now if $b_k=0$![]() for all $k\in \{1,2,\ldots,l\}$
for all $k\in \{1,2,\ldots,l\}$![]() , then we can replace $\boldsymbol {a}$
, then we can replace $\boldsymbol {a}$![]() and $\boldsymbol {b}$
and $\boldsymbol {b}$![]() by $(a_{l+1},a_{l+2},\ldots, a_{n})$
by $(a_{l+1},a_{l+2},\ldots, a_{n})$![]() and $(b_{l+1},b_{l+2},\ldots,b_{n})$
and $(b_{l+1},b_{l+2},\ldots,b_{n})$![]() , respectively, in (3.1),(3.2) and (3.3), and by the same analysis as above we can ensure that this case never exists. Note that if $b_k=0$
, respectively, in (3.1),(3.2) and (3.3), and by the same analysis as above we can ensure that this case never exists. Note that if $b_k=0$![]() for $l+1\leq k\leq n$
for $l+1\leq k\leq n$![]() , then for each real number $t$
, then for each real number $t$![]() , from (3.2), we have $(1+|t|^q)^{p/q}=1+|t|^p$
, from (3.2), we have $(1+|t|^q)^{p/q}=1+|t|^p$![]() , which is obviously not true. Therefore, for some $k$
, which is obviously not true. Therefore, for some $k$![]() with $1\leq k\leq l,$
with $1\leq k\leq l,$![]() $b_k$
$b_k$![]() is non-zero and for some $s$
is non-zero and for some $s$![]() with $l+1\leq s\leq n,$
with $l+1\leq s\leq n,$![]() $b_s$
$b_s$![]() is also non-zero. Thus, for the scalar field $\mathbb {K}=\mathbb {R}$
is also non-zero. Thus, for the scalar field $\mathbb {K}=\mathbb {R}$![]() and $q\in (0,\infty )$
and $q\in (0,\infty )$![]() or $\mathbb {K}=\mathbb {C}$
or $\mathbb {K}=\mathbb {C}$![]() and $q\in (0,\infty )\setminus 2\mathbb {N}$
and $q\in (0,\infty )\setminus 2\mathbb {N}$![]() , from (3.2), we get
, from (3.2), we get

Note that the right-hand side of (3.7) is real-analytic in a small neighbourhood of $0$![]() , but by lemma 2.5, the left-hand side is not differentiable at $0$
, but by lemma 2.5, the left-hand side is not differentiable at $0$![]() , which leads to a contradiction. This completes the proof of the theorem.
, which leads to a contradiction. This completes the proof of the theorem.
Remark 3.1 If we consider $\boldsymbol {a},\boldsymbol {b}\in \ell _p^n(\mathbb {C})$![]() with $a_k\neq 0, 1\leq k \leq n$
with $a_k\neq 0, 1\leq k \leq n$![]() , such that (3.1) holds. Then, it may happen that $\left.\frac {{\rm d}^2}{{\rm d}t^2}\right |_{t=0}{\lVert }{\boldsymbol {a}+t\boldsymbol {b}}{\rVert }_p^p=0$
, such that (3.1) holds. Then, it may happen that $\left.\frac {{\rm d}^2}{{\rm d}t^2}\right |_{t=0}{\lVert }{\boldsymbol {a}+t\boldsymbol {b}}{\rVert }_p^p=0$![]() . Indeed, let $\boldsymbol a=n^{-\frac {1}{p}}(1,1,\ldots,1)$
. Indeed, let $\boldsymbol a=n^{-\frac {1}{p}}(1,1,\ldots,1)$![]() , $\boldsymbol b=\frac {n^{-\frac {1}{p}}}{\sqrt {2-p}}(1+i\sqrt {1-p}, \ldots, 1+i\sqrt {1-p})$
, $\boldsymbol b=\frac {n^{-\frac {1}{p}}}{\sqrt {2-p}}(1+i\sqrt {1-p}, \ldots, 1+i\sqrt {1-p})$![]() . Then, note that $\|\boldsymbol a\|_p=\|\boldsymbol b\|_p=1$
. Then, note that $\|\boldsymbol a\|_p=\|\boldsymbol b\|_p=1$![]() , and
, and

So in this case from (3.5), we can't conclude anything about isometric embeddability of $\ell _q^m(\mathbb {C})$![]() into $\ell _p^n(\mathbb {C})$
into $\ell _p^n(\mathbb {C})$![]() as the above proof breaks down at 3.6.
as the above proof breaks down at 3.6.
4. Isometric embeddability $S_q^m\to S_p^n$ as non-commutative quasi-Banach spaces
as non-commutative quasi-Banach spaces
In this section, we study when $S_q^m$![]() embeds isometrically into $S_p^n$
embeds isometrically into $S_p^n$![]() as quasi-Banach spaces. We also give applications of our result to non-commutative $L_p$
as quasi-Banach spaces. We also give applications of our result to non-commutative $L_p$![]() -spaces. We begin recalling the concepts of operator derivatives and multiple operator integrals which were used in [Reference Chattopadhyay, Hong, Pal, Pradhan and Ray6].
-spaces. We begin recalling the concepts of operator derivatives and multiple operator integrals which were used in [Reference Chattopadhyay, Hong, Pal, Pradhan and Ray6].
4.1. Operator derivatives in $\ell _2^m$ in terms of multiple operator integrals
in terms of multiple operator integrals
Definition 4.1 Let $M_0,M_1,\ldots,M_n$![]() be self-adjoint operators on $\ell _2^m$
be self-adjoint operators on $\ell _2^m$![]() , let $\mathfrak {e}^{(j)}=\{\mathfrak {e}_i^{(j)}\}_{i=1}^{m}$
, let $\mathfrak {e}^{(j)}=\{\mathfrak {e}_i^{(j)}\}_{i=1}^{m}$![]() be an orthonormal basis of eigenvectors of $M_j$
be an orthonormal basis of eigenvectors of $M_j$![]() , and let $\boldsymbol {\lambda }^{(j)}=(\lambda _i^{(j)})_{i=1}^{m}$
, and let $\boldsymbol {\lambda }^{(j)}=(\lambda _i^{(j)})_{i=1}^{m}$![]() be the corresponding $m$
be the corresponding $m$![]() -tuple of eigenvalues for $j=0,1,\ldots,n$
-tuple of eigenvalues for $j=0,1,\ldots,n$![]() . Let $\Phi :\mathbb {R}^{n+1}\to \mathbb {C}$
. Let $\Phi :\mathbb {R}^{n+1}\to \mathbb {C}$![]() . We define
. We define
by

for any $n$![]() -tuple $(N_1,N_2,\ldots,N_n)$
-tuple $(N_1,N_2,\ldots,N_n)$![]() in $\mathcal {B}(\ell _2^m)$
in $\mathcal {B}(\ell _2^m)$![]() , where $P_{\mathfrak {e}_{i_k}^{(k)}}$
, where $P_{\mathfrak {e}_{i_k}^{(k)}}$![]() is the orthogonal projection of $\ell _2^m$
is the orthogonal projection of $\ell _2^m$![]() onto the subspace spanned by the vectors $\{\mathfrak {e}_{i_k}^{(k)}\}$
onto the subspace spanned by the vectors $\{\mathfrak {e}_{i_k}^{(k)}\}$![]() . The operator $T^{M_0,M_1,\ldots,M_n}_\Phi$
. The operator $T^{M_0,M_1,\ldots,M_n}_\Phi$![]() is a discrete version of a multiple operator integral and the function $\Phi$
is a discrete version of a multiple operator integral and the function $\Phi$![]() is called the symbol of the operator $T^{M_0,M_1,\ldots,M_n}_\Phi$
is called the symbol of the operator $T^{M_0,M_1,\ldots,M_n}_\Phi$![]() .
.
For additional information on discrete multiple operator integral and related topics, we refer [Reference Skripka and Tomskova43, chapter 4].
Throughout this paper, we denote by $C^k(\mathbb {R})$![]() to be the space of all $k$
to be the space of all $k$![]() -times differentiable functions which also has continuous $k$
-times differentiable functions which also has continuous $k$![]() -th derivative, where $k\in \mathbb {N}\cup \{0\}$
-th derivative, where $k\in \mathbb {N}\cup \{0\}$![]() . Recall that the divided difference of order $r$
. Recall that the divided difference of order $r$![]() is an operation on a function $f\in C^k(\mathbb {R})$
is an operation on a function $f\in C^k(\mathbb {R})$![]() defined recursively as follows:
defined recursively as follows:

We recall the formulae for operator derivatives in terms of multiple operator integrals.
Theorem 4.2 [Reference Skripka and Tomskova43, theorem 5.3.2] Let $M,N\in M_n^{sa}$![]() and $f\in C^r(\mathbb {R}), r\in \mathbb {N}$
and $f\in C^r(\mathbb {R}), r\in \mathbb {N}$![]() . Then, the function $\mathbb {R} \ni t\mapsto f(M+tN)$
. Then, the function $\mathbb {R} \ni t\mapsto f(M+tN)$![]() is $r$
is $r$![]() -times differentiable in the operator norm and the $r$
-times differentiable in the operator norm and the $r$![]() -th order derivative is given by the formula
-th order derivative is given by the formula

and hence

By applying theorem 4.2, one can get the following first-order derivative formula; however, we refer to this formula here because this formula can also be proved by a simple application of the Kato–Rellich theorem.
Proposition 4.3 Let $A,B\in M_n^{sa}$![]() with $A$
with $A$![]() is invertible and $0< p\leq 1$
is invertible and $0< p\leq 1$![]() , then
, then
Proof. The result follows from the same lines of proof of [Reference Chattopadhyay, Hong, Pal, Pradhan and Ray6, proposition 2.6].
4.2. Reduction to self-adjoint case
We now state the following lemma, which reduces our problem to the self-adjoint case. The following result is a straightforward generalization of [Reference Chattopadhyay, Hong, Pal, Pradhan and Ray6, lemma 2.7]. Hence we omit the proof of the following lemma.
Lemma 4.4 Let $0< q \leq \infty$![]() , $0< p<1$
, $0< p<1$![]() . Let $T:\ell _q^2\to S_p(\ell _2^n)$
. Let $T:\ell _q^2\to S_p(\ell _2^n)$![]() with $T(e_1)=A,$
with $T(e_1)=A,$![]() $T(e_2)=B$
$T(e_2)=B$![]() be an isometry. Then,
be an isometry. Then,
is again an isometry, where
Definition 4.5 Let $0< q \leq \infty$![]() , $0< p\leq \infty$
, $0< p\leq \infty$![]() , and $p\neq q$
, and $p\neq q$![]() . Let $A,B\in \mathcal {B}(\ell _2^n).$
. Let $A,B\in \mathcal {B}(\ell _2^n).$![]() We say $(A,B)$
We say $(A,B)$![]() has $(\mathbf {I}_{q,p})$
has $(\mathbf {I}_{q,p})$![]() if
if
• with respect to the standard basis, $A$
 is a diagonal matrix with all entries real and $B$
is a diagonal matrix with all entries real and $B$ is self-adjoint,
is self-adjoint,• ${\lVert }{A}{\rVert }_p={\lVert }{B}{\rVert }_p=1$
 ,
,• ${\lVert }{A+tB}{\rVert }_p=\|(1,t)\|_q$
 , for all $t\in \mathbb {R}$
, for all $t\in \mathbb {R}$ .
.
We prove the following lemma.
Lemma 4.6 Let $0< q \leq \infty$![]() , $0< p<1$
, $0< p<1$![]() , $p\neq q$
, $p\neq q$![]() . Assume that $A, B\in L_p(\mathcal {M})$
. Assume that $A, B\in L_p(\mathcal {M})$![]() are self-adjoint elements with $\|A\|_p=\|B\|_p=1$
are self-adjoint elements with $\|A\|_p=\|B\|_p=1$![]() and ${\lVert }{A+tB}{\rVert }_p=\|(1,t)\|_q$
and ${\lVert }{A+tB}{\rVert }_p=\|(1,t)\|_q$![]() , for all $t\in \mathbb {R}$
, for all $t\in \mathbb {R}$![]() . Then, we must have $AB\neq 0.$
. Then, we must have $AB\neq 0.$![]()
Proof. Suppose $AB=0$![]() . Then, $A$
. Then, $A$![]() and $B$
and $B$![]() have disjoint supports. It follows that $\|A+tB\|_p^p=\|A\|_p^p+|t|^p\|B\|_p^p$
have disjoint supports. It follows that $\|A+tB\|_p^p=\|A\|_p^p+|t|^p\|B\|_p^p$![]() . Note that $\|A\|_p=\|B\|_p=1$
. Note that $\|A\|_p=\|B\|_p=1$![]() . Thus $\|A+tB\|_p^p=1+|t|^p.$
. Thus $\|A+tB\|_p^p=1+|t|^p.$![]() But for each $t\in \mathbb {R}$
But for each $t\in \mathbb {R}$![]() , the identity $(1+|t|^q)^{1/q}=(1+|t|^p)^{1/p}$
, the identity $(1+|t|^q)^{1/q}=(1+|t|^p)^{1/p}$![]() is not true, which leads to a contradiction.
is not true, which leads to a contradiction.
Due to the above, we have the following necessary condition for existence of an isometric embedding of $S_q^m$![]() into $S_p^n$
into $S_p^n$![]() for $0< q \leq \infty$
for $0< q \leq \infty$![]() , $0< p<1$
, $0< p<1$![]() , $p\neq q$
, $p\neq q$![]() .
.
Corollary 4.7 Let $0< q \leq \infty$![]() , $0< p<1$
, $0< p<1$![]() , $p\neq q$
, $p\neq q$![]() and $(A,B)$
and $(A,B)$![]() has $(\mathbf {I}_{q,p})$
has $(\mathbf {I}_{q,p})$![]() . Then, we must have that $AB\neq 0$
. Then, we must have that $AB\neq 0$![]() .
.
The following theorem is one of the main result of this section. One of the main difficulties we face to prove the non-existence of isometric embedding is the nature of differentiability of the map $t\mapsto \|A+tB\|_p^p$![]() at $t=0,1$
at $t=0,1$![]() , which is keenly related to the multiplicity of zeros of the real-analytic eigenvalues of $A+tB$
, which is keenly related to the multiplicity of zeros of the real-analytic eigenvalues of $A+tB$![]() at $t=0$
at $t=0$![]() and $t=1$
and $t=1$![]() , where $(A,B)$
, where $(A,B)$![]() has $(\mathbf {I}_{q,p})$
has $(\mathbf {I}_{q,p})$![]() . We closely examine the multiplicity of zeros and compute the derivatives using the Kato-Rellich theorem and multiple operator integrals. This helps us to analyse the power-series of various analytic functions and compare them carefully. We need to use repeatedly the Kato–Rellich theorem and compare the coefficients arising in the series expansion. This also leads to various intricate computations which are combinatorial in nature.
. We closely examine the multiplicity of zeros and compute the derivatives using the Kato-Rellich theorem and multiple operator integrals. This helps us to analyse the power-series of various analytic functions and compare them carefully. We need to use repeatedly the Kato–Rellich theorem and compare the coefficients arising in the series expansion. This also leads to various intricate computations which are combinatorial in nature.
Theorem 4.8 Let $0< p\neq q<1$![]() and $2\leq m\leq n<\infty$
and $2\leq m\leq n<\infty$![]() . Then, there is no isometric embedding of $S_q^m$
. Then, there is no isometric embedding of $S_q^m$![]() into $S_p^n$
into $S_p^n$![]() .
.
Proof. On the contrary, suppose that there exists an isometric embedding $S_q^m$![]() into $S_p^n$
into $S_p^n$![]() . Then, by lemma 2.2, we have $p< q$
. Then, by lemma 2.2, we have $p< q$![]() . Therefore, by lemma 4.4, we may assume that there exists a diagonal self-adjoint matrix $A$
. Therefore, by lemma 4.4, we may assume that there exists a diagonal self-adjoint matrix $A$![]() and a self-adjoint matrix $B$
and a self-adjoint matrix $B$![]() in $S_p^n$
in $S_p^n$![]() such that $(A, B)$
such that $(A, B)$![]() has $(\mathbf {I}_{q,p})$
has $(\mathbf {I}_{q,p})$![]() . In particular, for any real number $t$
. In particular, for any real number $t$![]() , we have the identity
, we have the identity
In a small neighbourhood $\Omega$![]() of zero, by Kato–Rellich theorem 2.4, there exist $n$
of zero, by Kato–Rellich theorem 2.4, there exist $n$![]() real-analytic functions $\lambda _1(\cdot ), \lambda _2(\cdot ),\ldots, \lambda _n(\cdot )$
real-analytic functions $\lambda _1(\cdot ), \lambda _2(\cdot ),\ldots, \lambda _n(\cdot )$![]() on $\Omega$
on $\Omega$![]() such that they are complete set of eigenvalues of $A+tB$
such that they are complete set of eigenvalues of $A+tB$![]() for $t\in \Omega$
for $t\in \Omega$![]() . So for $t\in \Omega$
. So for $t\in \Omega$![]() , from (4.4), we have
, from (4.4), we have

If $\lambda _k(0)\neq 0$![]() for all $1\leq k\leq n$
for all $1\leq k\leq n$![]() , that is if $A$
, that is if $A$![]() is invertible, then the right-hand side of (4.5) is a real-analytic function in $\Omega$
is invertible, then the right-hand side of (4.5) is a real-analytic function in $\Omega$![]() but the left-hand side of (4.5) is not analytic in $\Omega$
but the left-hand side of (4.5) is not analytic in $\Omega$![]() . So $A$
. So $A$![]() must be a singular matrix. Again from (4.5), it is clear that not all $\lambda _k(0)$
must be a singular matrix. Again from (4.5), it is clear that not all $\lambda _k(0)$![]() are zero. So there is a non-empty proper subset $O\subset \{1,2,\ldots,n\}$
are zero. So there is a non-empty proper subset $O\subset \{1,2,\ldots,n\}$![]() such that $\lambda _k(0)=0$
such that $\lambda _k(0)=0$![]() for $k\in O$
for $k\in O$![]() , and $\lambda _k(0)\neq 0$
, and $\lambda _k(0)\neq 0$![]() for $k\in \{1,2,\ldots,n\}\setminus O$
for $k\in \{1,2,\ldots,n\}\setminus O$![]() . Since the quasi-norm $\|\cdot \|_p$
. Since the quasi-norm $\|\cdot \|_p$![]() is unitary invariant, we may assume that there exists an $l\in \{1,2,\ldots,n-1\}$
is unitary invariant, we may assume that there exists an $l\in \{1,2,\ldots,n-1\}$![]() such that $\lambda _k(0)=0$
such that $\lambda _k(0)=0$![]() for $1\leq k\leq l$
for $1\leq k\leq l$![]() , and $\lambda _k(0)\neq 0$
, and $\lambda _k(0)\neq 0$![]() for $l+1\leq k\leq n$
for $l+1\leq k\leq n$![]() . Note that if some $\lambda _i(t)$
. Note that if some $\lambda _i(t)$![]() are identically zero, we can neglect those as they have no contribution in $\|A+tB\|_p$
are identically zero, we can neglect those as they have no contribution in $\|A+tB\|_p$![]() . Therefore, we may also assume that all $\lambda _k(t)$
. Therefore, we may also assume that all $\lambda _k(t)$![]() are non-zero analytic functions in $\Omega$
are non-zero analytic functions in $\Omega$![]() . Let $m_k$
. Let $m_k$![]() be the multiplicity of zero at $0$
be the multiplicity of zero at $0$![]() of the function $\lambda _k(t)$
of the function $\lambda _k(t)$![]() for $1\leq k\leq l$
for $1\leq k\leq l$![]() . Then,
. Then,
where $\mu _k(\cdot )$![]() are analytic in $\Omega$
are analytic in $\Omega$![]() . For further progression, let us define
. For further progression, let us define

It is clear that $\Psi (\cdot )$![]() is analytic in $\Omega$
is analytic in $\Omega$![]() and $\Psi (0)=0$
and $\Psi (0)=0$![]() . Then, $\Psi (t)=t\Psi _{1}(t)$
. Then, $\Psi (t)=t\Psi _{1}(t)$![]() , where $\Psi _{1}(\cdot )$
, where $\Psi _{1}(\cdot )$![]() is a analytic function in $\Omega$
is a analytic function in $\Omega$![]() . Applying (4.6) and (4.7) in (4.5), we have
. Applying (4.6) and (4.7) in (4.5), we have

Now we will reach our goal through case-by-case analysis.
Case I: Let $m_kp>1$![]() for $1\leq k\leq l$
for $1\leq k\leq l$![]() . Then, the right-hand side of (4.8) is differentiable at $0$
. Then, the right-hand side of (4.8) is differentiable at $0$![]() but the left-hand side of (4.8) is not differentiable at $0$
but the left-hand side of (4.8) is not differentiable at $0$![]() . So this case is not possible.
. So this case is not possible.
Case II: Suppose at least one of $m_kp=1$![]() for $1\leq k\leq l$
for $1\leq k\leq l$![]() . Without loss of generality, we assume that $m_1p=1.$
. Without loss of generality, we assume that $m_1p=1.$![]() Note that as $\mu _k(0)\neq 0$
Note that as $\mu _k(0)\neq 0$![]() , $|\mu _k(t)|^p$
, $|\mu _k(t)|^p$![]() are analytic in $\Omega$
are analytic in $\Omega$![]() for $1\leq k\leq l$
for $1\leq k\leq l$![]() . So we can express $|\mu _k(t)|^p$
. So we can express $|\mu _k(t)|^p$![]() as
as
where $\xi _k(\cdot )$![]() are some analytic function in the small neighbourhood $\Omega$
are some analytic function in the small neighbourhood $\Omega$![]() of $0$
of $0$![]() . Let $\boldsymbol {m}$
. Let $\boldsymbol {m}$![]() be the least positive integer such that $\boldsymbol mq> 1$
be the least positive integer such that $\boldsymbol mq> 1$![]() .
.
Sub-case I: Suppose $l\geq 3$![]() , $m_1p=m_2p=\cdots =m_jp=1$
, $m_1p=m_2p=\cdots =m_jp=1$![]() , $m_{j+1}p, \ldots, m_ip<1$
, $m_{j+1}p, \ldots, m_ip<1$![]() and $m_{i+1}p,\ldots,m_lp>1$
and $m_{i+1}p,\ldots,m_lp>1$![]() for some $j\in \{1,2,\ldots, l-2\}$
for some $j\in \{1,2,\ldots, l-2\}$![]() , and $i\in \{j+1\ldots, l-1\}$
, and $i\in \{j+1\ldots, l-1\}$![]() . Combining (4.8) and (4.9), we have
. Combining (4.8) and (4.9), we have

where $\alpha _k$![]() is the coefficient of $|t|^{kq}$
is the coefficient of $|t|^{kq}$![]() in the binomial expansion of $(1+|t|^q)^{p/q}$
in the binomial expansion of $(1+|t|^q)^{p/q}$![]() for $|t|<1$
for $|t|<1$![]() . That is, $\alpha _k=(\begin {matrix} p/q\\ k \end {matrix})=\frac {p/q(p/q-1)\cdots (p/q-k+1)}{k!}$
. That is, $\alpha _k=(\begin {matrix} p/q\\ k \end {matrix})=\frac {p/q(p/q-1)\cdots (p/q-k+1)}{k!}$![]() , $k\in \mathbb {N}$
, $k\in \mathbb {N}$![]() .
.
From (4.10), we have

In this case, the right-hand side of the above equation (4.11) is differentiable at $0$![]() . Since $p< q$
. Since $p< q$![]() , so $\alpha _{2}<0$
, so $\alpha _{2}<0$![]() . Therefore, by the similar lines of argument as given in the proof of lemma 2.5, the left-hand side of (4.11) is not differentiable at $0$
. Therefore, by the similar lines of argument as given in the proof of lemma 2.5, the left-hand side of (4.11) is not differentiable at $0$![]() . Hence, this case does not exist.
. Hence, this case does not exist.
Sub-case II: Suppose $l\geq 2$![]() , $m_1p=\cdots =m_jp=1$
, $m_1p=\cdots =m_jp=1$![]() and $m_{j+1}p,\ldots,m_lp<1$
and $m_{j+1}p,\ldots,m_lp<1$![]() for some $j\in \{1,\ldots,l-1\}$
for some $j\in \{1,\ldots,l-1\}$![]() . Then, for $t\in \Omega$
. Then, for $t\in \Omega$![]() , from (4.10), we get
, from (4.10), we get

It is clear that the left side of equation (4.12) is not differentiable at $0$![]() , but the other side is differentiable at $0$
, but the other side is differentiable at $0$![]() . So equation (4.12) never exists in $\Omega$
. So equation (4.12) never exists in $\Omega$![]() .
.
Sub-case III: Suppose $l\geq 2$![]() , $m_1p=\cdots =m_jp=1$
, $m_1p=\cdots =m_jp=1$![]() , $m_{j+1}p,\ldots,m_lp>1$
, $m_{j+1}p,\ldots,m_lp>1$![]() for some $j\in \{1,\ldots,l-1\}$
for some $j\in \{1,\ldots,l-1\}$![]() . Again from (4.10), we have
. Again from (4.10), we have

By a similar argument as given for the non-existence of equation (4.12), we conclude the non-existence of equation (4.13).
Sub-case IV: Let $m_1p=\cdots =m_lp=1$![]() . By similar argument as given in the above sub-case, we conclude that this situation never exists.
. By similar argument as given in the above sub-case, we conclude that this situation never exists.
Case III: Let $m_kp<1$![]() for $1\leq k\leq l$
for $1\leq k\leq l$![]() . From (4.10), we have
. From (4.10), we have

Note that the right-hand side of (4.14) is differentiable at $0$![]() . Therefore, the existence of equation (4.14) implies that the left-hand side of (4.14) is also differentiable at $0$
. Therefore, the existence of equation (4.14) implies that the left-hand side of (4.14) is also differentiable at $0$![]() .
.
Sub-case I: Let $2q\leq 1$![]() . The necessary condition for differentiability of the left-hand side of (4.14) is that there exists a non-empty proper subset $I\subset \{1,2,\ldots,l\}$
. The necessary condition for differentiability of the left-hand side of (4.14) is that there exists a non-empty proper subset $I\subset \{1,2,\ldots,l\}$![]() such that
such that
(a) $m_kp=2q,\ k\in I,$
 and $\alpha _2=\sum \limits _{k\in I}|\mu _k(0)|^p.$
and $\alpha _2=\sum \limits _{k\in I}|\mu _k(0)|^p.$
By lemma 2.2, we obtain $\frac {p}{q}<1$![]() . Hence, $\alpha _2=\frac {1}{2!}\frac {p}{q}(\frac {p}{q}-1)<0$
. Hence, $\alpha _2=\frac {1}{2!}\frac {p}{q}(\frac {p}{q}-1)<0$![]() , but $\sum \limits _{k\in I}|\mu _k(0)|^p>0$
, but $\sum \limits _{k\in I}|\mu _k(0)|^p>0$![]() . So the above identity (A) is not true. Hence, equation (4.14) never exists in the small neighbourhood $\Omega$
. So the above identity (A) is not true. Hence, equation (4.14) never exists in the small neighbourhood $\Omega$![]() , which is a contradiction.
, which is a contradiction.
Sub-case II: Let $2q> 1$![]() . In this case, the necessary condition for differentiability of the left-hand side of (4.14) is that
. In this case, the necessary condition for differentiability of the left-hand side of (4.14) is that
(a) $m_kp=q,\ k\in \{1,2,\ldots,l\}, \text {and}\ \alpha _1=\sum \limits _{k=1}^{l}|\mu _k(0)|^p$
 .
.
Suppose the above necessary condition (a) holds, then from (4.14), we have,

Taking limit $t\to 0$![]() on both sides of (4.15), we have $\Psi _{1}(0)=0$
on both sides of (4.15), we have $\Psi _{1}(0)=0$![]() which implies $\Psi _{1}(t)=t\Psi _{2}(t)$
which implies $\Psi _{1}(t)=t\Psi _{2}(t)$![]() for some analytic function $\Psi _{2}(t)$
for some analytic function $\Psi _{2}(t)$![]() in $\Omega$
in $\Omega$![]() of $0$
of $0$![]() . Let $\xi _k(t)=\xi _k(0)+t\,\eta _k(t), 1\leq k\leq l$
. Let $\xi _k(t)=\xi _k(0)+t\,\eta _k(t), 1\leq k\leq l$![]() and $\eta _k$
and $\eta _k$![]() are some analytic functions in $\Omega$
are some analytic functions in $\Omega$![]() . Then, from (4.15), we have
. Then, from (4.15), we have

Observe that the right-hand side of (4.16) is bounded around $0$![]() but the left-hand side is unbounded around $0$
but the left-hand side is unbounded around $0$![]() , which leads to a contradiction.
, which leads to a contradiction.
Hence, case III does not exist.
Case IV: Suppose $l\geq 2$![]() and there are some $m_kp$
and there are some $m_kp$![]() which are strictly less than $1$
which are strictly less than $1$![]() and rest are strictly greater than $1$
and rest are strictly greater than $1$![]() . We may assume $m_1p,\ldots,m_ip<1$
. We may assume $m_1p,\ldots,m_ip<1$![]() and $m_{i+1}p,\ldots,m_lp>1$
and $m_{i+1}p,\ldots,m_lp>1$![]() for some $i\in \,\{1,2,\ldots,l-1\}$
for some $i\in \,\{1,2,\ldots,l-1\}$![]() . From (4.10), we obtain
. From (4.10), we obtain

Then, we again consider the following two sub-cases:
Sub-case I: Let $2q\leq 1$![]() . By the similar lines of argument as given in sub-case I of sase III of this proof, we conclude that this situation never exists.
. By the similar lines of argument as given in sub-case I of sase III of this proof, we conclude that this situation never exists.
Sub-case II: Let $2q> 1$![]() . In this case, the necessary condition for differentiability of the left-hand side of (4.14) is that
. In this case, the necessary condition for differentiability of the left-hand side of (4.14) is that
(1) $m_kp=q,~~ k\in \{1,2,\ldots,i\}, \text { and } \alpha _1=\sum \limits _{k=1}^{i}|\mu _k(0)|^p$
 .
.
Suppose the above necessary condition (1) holds, then from (4.17), we have,

Since $2q>1$![]() and $m_kp>1$
and $m_kp>1$![]() for all $i+1\leq k\leq l$
for all $i+1\leq k\leq l$![]() , then taking limit $t\to 0$
, then taking limit $t\to 0$![]() on both sides of (4.18), we have $\Psi _1(0)=0$
on both sides of (4.18), we have $\Psi _1(0)=0$![]() . Let $\Psi _{1}(t)=t\Psi _{2}(t)$
. Let $\Psi _{1}(t)=t\Psi _{2}(t)$![]() . Let $\xi _k(t)=\xi _k(0)+t\,\eta _k(t), 1\leq k\leq l$
. Let $\xi _k(t)=\xi _k(0)+t\,\eta _k(t), 1\leq k\leq l$![]() and $\eta _k$
and $\eta _k$![]() are some analytic functions in $\Omega$
are some analytic functions in $\Omega$![]() . Then, from (4.18), we get
. Then, from (4.18), we get

Note that as $\alpha _{2}<0$![]() , the left-hand side of (4.19) is unbounded near $0$
, the left-hand side of (4.19) is unbounded near $0$![]() but the right-hand side of (4.19) is bounded near $0$
but the right-hand side of (4.19) is bounded near $0$![]() and tends to $\Psi _2(0)$
and tends to $\Psi _2(0)$![]() as $t\to 0$
as $t\to 0$![]() , which implies that this case never exists.
, which implies that this case never exists.
Therefore, from all the above cases, we conclude that there does not exist any isometric embedding of $S_q^m$![]() into $S_p^n$
into $S_p^n$![]() for $0< q\neq p<1$
for $0< q\neq p<1$![]() . This completes the proof of the theorem.
. This completes the proof of the theorem.
Theorem 4.9 Let $(q,p)\in (1,2)\times (0,1)$![]() and $2\leq m\leq n<\infty$
and $2\leq m\leq n<\infty$![]() . Then, there does not exist any isometric embedding of $S_q^m$
. Then, there does not exist any isometric embedding of $S_q^m$![]() into $S_p^n$
into $S_p^n$![]() with $p\neq q$
with $p\neq q$![]() .
.
Proof. Suppose that there is an isometric embedding of $S_q^m$![]() into $S_p^n$
into $S_p^n$![]() . Then, there exist $A,B\in S_p^n$
. Then, there exist $A,B\in S_p^n$![]() such that $(A,B)$
such that $(A,B)$![]() has $(\mathbf {I}_{q,p})$
has $(\mathbf {I}_{q,p})$![]() . Here, we use the same notations used in the proof of theorem 4.8. So the existence of isometric embedding implies that identity (4.5) is true in a small neighbourhood $\Omega$
. Here, we use the same notations used in the proof of theorem 4.8. So the existence of isometric embedding implies that identity (4.5) is true in a small neighbourhood $\Omega$![]() of $0$
of $0$![]() . Note that if $A$
. Note that if $A$![]() is invertible, then the right-hand side of (4.5) is real-analytic but the left-hand side of (4.5) is not real-analytic in $\Omega$
is invertible, then the right-hand side of (4.5) is real-analytic but the left-hand side of (4.5) is not real-analytic in $\Omega$![]() . So the matrix $A$
. So the matrix $A$![]() is not invertible. Therefore, by the similar argument as given in the proof of theorem (4.8), we can deduce (4.8) from identity (4.5). In other words, we have the following.
is not invertible. Therefore, by the similar argument as given in the proof of theorem (4.8), we can deduce (4.8) from identity (4.5). In other words, we have the following.

Note that the left-hand side of (4.20) is one time differentiable at $0$![]() , and one time differentiability of (4.20) implies that some of $m_kp$
, and one time differentiability of (4.20) implies that some of $m_kp$![]() are in $(1,2)$
are in $(1,2)$![]() and rest belong to $[2,\infty )$
and rest belong to $[2,\infty )$![]() . Since $\|\cdot \|_p$
. Since $\|\cdot \|_p$![]() is unitary invariant, we may assume that there exists $i\in \{1,2,\ldots,l-1\}$
is unitary invariant, we may assume that there exists $i\in \{1,2,\ldots,l-1\}$![]() such that
such that
A simple calculation shows that $\Psi _{1}(0)=0$![]() . Let $|\mu _k(t)|^p=|\mu _k(0)|^p+ t\xi _k(t)$
. Let $|\mu _k(t)|^p=|\mu _k(0)|^p+ t\xi _k(t)$![]() , $1\leq k\leq l$
, $1\leq k\leq l$![]() , and $\Psi _{1}(t)=t\Psi _{2}(t)$
, and $\Psi _{1}(t)=t\Psi _{2}(t)$![]() , where $\xi _k(\cdot )$
, where $\xi _k(\cdot )$![]() and $\Psi _{2}(\cdot )$
and $\Psi _{2}(\cdot )$![]() are some analytic functions in $\Omega$
are some analytic functions in $\Omega$![]() . Then, from (4.20), we have
. Then, from (4.20), we have

Observe that if $m_kp\neq q$![]() for some $k\in \{1,\ldots,i\}$
for some $k\in \{1,\ldots,i\}$![]() , then the left-hand side of above equation (4.21) becomes unbounded near $0$
, then the left-hand side of above equation (4.21) becomes unbounded near $0$![]() but the right-hand side of (4.21) is bounded and going to $\Psi _2(0)$
but the right-hand side of (4.21) is bounded and going to $\Psi _2(0)$![]() as $t\to \infty$
as $t\to \infty$![]() . So $m_kp=q$
. So $m_kp=q$![]() for all $k\in \{1,\ldots,i\}$
for all $k\in \{1,\ldots,i\}$![]() . Again by the same reason, we have $\alpha _1=\sum \limits _{k=1}^{i}|\mu _k(0)|^p$
. Again by the same reason, we have $\alpha _1=\sum \limits _{k=1}^{i}|\mu _k(0)|^p$![]() . Therefore, from (4.21), we have
. Therefore, from (4.21), we have

Now if there is a non-empty set $I\subseteq \{i+1,\ldots,l\}$![]() such that $m_kp=2$
such that $m_kp=2$![]() for $k\in I$
for $k\in I$![]() , then we can rewrite (4.22) as
, then we can rewrite (4.22) as

where $\tilde {\Psi }_{2}(t)=\Psi _{2}(t)+\sum _{k\in I} |\mu _k(t)|^p,\, t\in \Omega$![]() . Clearly, $\tilde {\Psi }_2(\cdot )$
. Clearly, $\tilde {\Psi }_2(\cdot )$![]() is analytic in $\Omega$
is analytic in $\Omega$![]() . Therefore, in (4.22), without loss of generality, we may assume that $m_kp>2$
. Therefore, in (4.22), without loss of generality, we may assume that $m_kp>2$![]() for all $i+1\leq k\leq l$
for all $i+1\leq k\leq l$![]() as $\Psi _2$
as $\Psi _2$![]() can be replaced by $\tilde {\Psi }_2$
can be replaced by $\tilde {\Psi }_2$![]() and other term can be modified accordingly. Taking limit $t\to 0$
and other term can be modified accordingly. Taking limit $t\to 0$![]() on both sides of (4.22), we conclude that $\Psi _{2}(0)=0$
on both sides of (4.22), we conclude that $\Psi _{2}(0)=0$![]() . Let $\xi _k(t)=\xi _k(0)+t\eta _k(t), 1\leq k\leq l$
. Let $\xi _k(t)=\xi _k(0)+t\eta _k(t), 1\leq k\leq l$![]() , and $\Psi _{2}(t)=t\Psi _{3}(t)$
, and $\Psi _{2}(t)=t\Psi _{3}(t)$![]() , where $\eta _k(\cdot )$
, where $\eta _k(\cdot )$![]() , and $\Psi _{3}(\cdot )$
, and $\Psi _{3}(\cdot )$![]() are some analytic functions in $\Omega$
are some analytic functions in $\Omega$![]() . Then, from (4.22), we have
. Then, from (4.22), we have

Case I: Let $1< q\leq \frac {3}{2}$![]() , then $2q-2\leq 1$
, then $2q-2\leq 1$![]() . Therefore, $|t|^{2q-1}$
. Therefore, $|t|^{2q-1}$![]() is not differentiable at $0$
is not differentiable at $0$![]() . Now if $m_kp>3$
. Now if $m_kp>3$![]() for all $k\in \{i+1,\ldots,l\}$
for all $k\in \{i+1,\ldots,l\}$![]() , then the right-hand side of (4.23) is differentiable at $0$
, then the right-hand side of (4.23) is differentiable at $0$![]() but the left-hand side of (4.23) is not differentiable at $0$
but the left-hand side of (4.23) is not differentiable at $0$![]() . So without loss of any generality, we may assume that there exists $j\in \{i+1,\ldots,l-1\}$
. So without loss of any generality, we may assume that there exists $j\in \{i+1,\ldots,l-1\}$![]() such that $m_kp\leq 3$
such that $m_kp\leq 3$![]() for $i+1\leq k\leq j$
for $i+1\leq k\leq j$![]() and $m_kp>3$
and $m_kp>3$![]() for $j+1\leq k\leq l$
for $j+1\leq k\leq l$![]() . Then, from (4.23), we have
. Then, from (4.23), we have

Note that the right-hand side of (4.24) is differentiable at $0,$![]() which forces us to conclude that there exists a non-empty subset $J\subseteq \{i+1,\ldots,j\}$
which forces us to conclude that there exists a non-empty subset $J\subseteq \{i+1,\ldots,j\}$![]() such that $m_kp=2q$
such that $m_kp=2q$![]() for $k\in J$
for $k\in J$![]() and $\alpha _{2}=\sum \limits _{k\in J} |\mu _k(0)|^p$
and $\alpha _{2}=\sum \limits _{k\in J} |\mu _k(0)|^p$![]() . But $\alpha _{2}<0$
. But $\alpha _{2}<0$![]() and $\sum \limits _{k\in J} |\mu _k(0)|^p>0$
and $\sum \limits _{k\in J} |\mu _k(0)|^p>0$![]() , which leads to a contradiction.
, which leads to a contradiction.
Case II: Let $\frac {3}{2}< q<2$![]() . Then, from (4.23), we have
. Then, from (4.23), we have

Let $A=\sum \limits _{k=1}^{i} \xi _k(0)$![]() , and $\eta _k(t)=\eta _k(0)+t\,\gamma _k(t),\, 1\leq k\leq l$
, and $\eta _k(t)=\eta _k(0)+t\,\gamma _k(t),\, 1\leq k\leq l$![]() , for some analytic function $\gamma _k(\cdot )$
, for some analytic function $\gamma _k(\cdot )$![]() in $\Omega$
in $\Omega$![]() . Now we rewrite the above equation (4.25) as
. Now we rewrite the above equation (4.25) as

If $m_kp\geq 4$![]() for $i+1\leq k\leq l$
for $i+1\leq k\leq l$![]() , then the right-hand side of (4.26) is differentiable but the left-hand side of (4.26) is not differentiable at $0$
, then the right-hand side of (4.26) is differentiable but the left-hand side of (4.26) is not differentiable at $0$![]() . So we may assume that there exist some $j\in \{i+1,\ldots,l-1\}$
. So we may assume that there exist some $j\in \{i+1,\ldots,l-1\}$![]() such that $2\leq m_kp<4$
such that $2\leq m_kp<4$![]() for $i+1\leq k\leq j,$
for $i+1\leq k\leq j,$![]() and $4\leq m_kp<\infty$
and $4\leq m_kp<\infty$![]() for $j+1\leq k\leq l.$
for $j+1\leq k\leq l.$![]() Then, from (4.26), we have
Then, from (4.26), we have

Here again observe that the right-hand side of (4.27) is differentiable at $0$![]() , which implies the differentiability of the left-hand side of (4.27), and consequently there exists a non-empty set $J\subseteq \{i+1,\ldots,j\}$
, which implies the differentiability of the left-hand side of (4.27), and consequently there exists a non-empty set $J\subseteq \{i+1,\ldots,j\}$![]() such that $m_kp=2q$
such that $m_kp=2q$![]() for all $k\in J$
for all $k\in J$![]() and $\alpha _{2}=\sum \limits _{k\in J}|\mu _k(0)|^p$
and $\alpha _{2}=\sum \limits _{k\in J}|\mu _k(0)|^p$![]() . But $\alpha _{2}<0,$
. But $\alpha _{2}<0,$![]() and $\sum \limits _{k\in J}|\mu _k(0)|^p\geq 0$
and $\sum \limits _{k\in J}|\mu _k(0)|^p\geq 0$![]() , which is a contradiction.
, which is a contradiction.
Hence, after analysing all the above cases, we conclude that there is no isometric embedding of $S_q^m$![]() into $S_p^n$
into $S_p^n$![]() . This completes the proof.
. This completes the proof.
Theorem 4.10 Let $p\in (0,1)\setminus \{\frac {1}{k}:k\in \mathbb {N}\}$![]() and $2\leq m\leq n<\infty$
and $2\leq m\leq n<\infty$![]() . Then, there is no isometric embedding of $S_1^m$
. Then, there is no isometric embedding of $S_1^m$![]() into $S_p^n$
into $S_p^n$![]() .
.
Proof. We will prove this result by contradiction. Suppose that there is an isometric embedding of $S_1^m$![]() into $S_p^n$
into $S_p^n$![]() . Here, in the proof, we use the same notation that is used in the proof of theorem 4.8. Therefore, we have identity (4.4) and consequently identity (4.5), that is we have
. Here, in the proof, we use the same notation that is used in the proof of theorem 4.8. Therefore, we have identity (4.4) and consequently identity (4.5), that is we have

It is easy to observe that not all $\lambda _k(0)$![]() vanish. The non-differentiability of the left-hand side of (4.28) at $0$
vanish. The non-differentiability of the left-hand side of (4.28) at $0$![]() forces that not all $\lambda _k(0)$
forces that not all $\lambda _k(0)$![]() are non-zero. Therefore, we may assume that there is some $l\in \{1,\ldots,n-1\}$
are non-zero. Therefore, we may assume that there is some $l\in \{1,\ldots,n-1\}$![]() such that $\lambda _k(0)=0$
such that $\lambda _k(0)=0$![]() for $1\leq k\leq l$
for $1\leq k\leq l$![]() and $\lambda _k(0)\neq 0$
and $\lambda _k(0)\neq 0$![]() for $l+1\leq k\leq n$
for $l+1\leq k\leq n$![]() . Hence, we have identity (4.8). That is
. Hence, we have identity (4.8). That is

Note that $m_kp\neq 1,\forall k\in \{1,\ldots,l\}$![]() as $p\in (0,1)\setminus \{\frac {1}{k}:k\in \mathbb {N}\}$
as $p\in (0,1)\setminus \{\frac {1}{k}:k\in \mathbb {N}\}$![]() . It is clear from the right-hand side of (4.29) that not all $m_kp>1$
. It is clear from the right-hand side of (4.29) that not all $m_kp>1$![]() , otherwise the right-hand side of (4.29) is differentiable at $0$
, otherwise the right-hand side of (4.29) is differentiable at $0$![]() but the left-hand side is not differentiable at $0$
but the left-hand side is not differentiable at $0$![]() . So there exists a non-empty subset $J\subseteq \{1,\ldots,l\}$
. So there exists a non-empty subset $J\subseteq \{1,\ldots,l\}$![]() such that $m_kp<1$
such that $m_kp<1$![]() for $k\in J$
for $k\in J$![]() and $m_kp>1$
and $m_kp>1$![]() for $k\in \{1,\ldots,l\}\setminus J$
for $k\in \{1,\ldots,l\}\setminus J$![]() . Therefore, from (4.29), we have
. Therefore, from (4.29), we have

Note that the left-hand side of (4.30) is not differentiable at $0$![]() but the right-hand side of (4.30) is differentiable at $0$
but the right-hand side of (4.30) is differentiable at $0$![]() , which contradicts our assumption. This completes the proof.
, which contradicts our assumption. This completes the proof.
Theorem 4.11 Let $p\in (0,1)\setminus \{\frac {1}{k}:k\in \mathbb {N}\}$![]() and $2\leq m\leq n<\infty$
and $2\leq m\leq n<\infty$![]() . Then, there is no isometric embedding of $S_\infty ^m$
. Then, there is no isometric embedding of $S_\infty ^m$![]() into $S_p^n$
into $S_p^n$![]() .
.
Proof. Suppose that there exists an isometric embedding $S_\infty ^m$![]() into $S_p^n$
into $S_p^n$![]() . Then, there exist $A$
. Then, there exist $A$![]() and $B$
and $B$![]() in $S_p^n$
in $S_p^n$![]() such that $A, B$
such that $A, B$![]() have $(\mathbf {I}_{\infty,p})$
have $(\mathbf {I}_{\infty,p})$![]() . Therefore, we have the following identity
. Therefore, we have the following identity
By the Kato–Rellich theorem 2.4, there exist $n$![]() real-analytic functions $\lambda _1(\cdot ), \lambda _2(\cdot ),\ldots, \lambda _n(\cdot )$
real-analytic functions $\lambda _1(\cdot ), \lambda _2(\cdot ),\ldots, \lambda _n(\cdot )$![]() in a small neighbourhood $U$
in a small neighbourhood $U$![]() of $1$
of $1$![]() such that they are complete set of eigenvalues of $A+tB$
such that they are complete set of eigenvalues of $A+tB$![]() for $t\in U$
for $t\in U$![]() . So for $t\in U$
. So for $t\in U$![]() , from (4.31), we have
, from (4.31), we have

If $\lambda _k(1)\neq 0$![]() for all $1\leq k\leq n$
for all $1\leq k\leq n$![]() , that is if $A+B$
, that is if $A+B$![]() is invertible, then the right-hand side of (4.32) is a real-analytic function in $U$
is invertible, then the right-hand side of (4.32) is a real-analytic function in $U$![]() but the left hand side of (4.32) is not analytic in $U$
but the left hand side of (4.32) is not analytic in $U$![]() . So $A+B$
. So $A+B$![]() is a singular matrix. In (4.32), note that not all $\lambda _k(1)$
is a singular matrix. In (4.32), note that not all $\lambda _k(1)$![]() are zero as $1=\sum _{k=1}^{n}|\lambda _k(1)|^p$
are zero as $1=\sum _{k=1}^{n}|\lambda _k(1)|^p$![]() . So without loss of generality, we may assume that there is a natural number $l\in \{1,2,\ldots,n\}$
. So without loss of generality, we may assume that there is a natural number $l\in \{1,2,\ldots,n\}$![]() such that $\lambda _k(1)=0$
such that $\lambda _k(1)=0$![]() for $1\leq k\leq l$
for $1\leq k\leq l$![]() and $\lambda _k(1)\neq 0$
and $\lambda _k(1)\neq 0$![]() for $l+1\leq k\leq n$
for $l+1\leq k\leq n$![]() . Note that if some $\lambda _i(t)$
. Note that if some $\lambda _i(t)$![]() is identically zero in $U$
is identically zero in $U$![]() , we can neglect that one as it has no contribution in $\|A+tB\|_p$
, we can neglect that one as it has no contribution in $\|A+tB\|_p$![]() . Therefore, we may also assume that all $\lambda _i(t)$
. Therefore, we may also assume that all $\lambda _i(t)$![]() are non-zero analytic functions in $U$
are non-zero analytic functions in $U$![]() . Let $m_k$
. Let $m_k$![]() be the multiplicity of zero at $1$
be the multiplicity of zero at $1$![]() of the function $\lambda _k(t)$
of the function $\lambda _k(t)$![]() for $1\leq k\leq l$
for $1\leq k\leq l$![]() . Let $\lambda _k(t)=(t-1)^{m_k}\mu _k(t), \mu _k(1)\neq 0,1\leq k\leq l$
. Let $\lambda _k(t)=(t-1)^{m_k}\mu _k(t), \mu _k(1)\neq 0,1\leq k\leq l$![]() , for some analytic function $\mu _k(\cdot )$
, for some analytic function $\mu _k(\cdot )$![]() in $U$
in $U$![]() . Then, from (4.32), we have,
. Then, from (4.32), we have,

Since the left-hand side of (4.33) is not differentiable at $1$![]() , not all $m_kp$
, not all $m_kp$![]() in (4.33) are greater than $1$
in (4.33) are greater than $1$![]() . So we may assume that there is a non-empty set $J\subseteq \{1,\ldots, l\}$
. So we may assume that there is a non-empty set $J\subseteq \{1,\ldots, l\}$![]() such that $m_kp<1$
such that $m_kp<1$![]() for $k\in J$
for $k\in J$![]() and $m_kp>1$
and $m_kp>1$![]() for $k\in \{1,\ldots, l\}\setminus J$
for $k\in \{1,\ldots, l\}\setminus J$![]() . Let $|\mu _k(t)|^p=|\mu _k(1)|^p+(t-1)\xi _k(t), k\in J$
. Let $|\mu _k(t)|^p=|\mu _k(1)|^p+(t-1)\xi _k(t), k\in J$![]() , where $\xi _k(\cdot )$
, where $\xi _k(\cdot )$![]() are some analytic function in $U$
are some analytic function in $U$![]() . Then, from (4.33), we have
. Then, from (4.33), we have

It is clear that the right-hand side of (4.34) is differentiable at $1$![]() but the left-hand side is not differentiable at $1$
but the left-hand side is not differentiable at $1$![]() , which leads to a contradiction. Therefore, there is no isometric embedding of $S_\infty ^m$
, which leads to a contradiction. Therefore, there is no isometric embedding of $S_\infty ^m$![]() into $S_p^n$
into $S_p^n$![]() . This completes the proof of the theorem.
. This completes the proof of the theorem.
The following Lemma is needed to prove our main result in this section.
Lemma 4.12 Let $0< q<\infty$![]() , $0< p<1$
, $0< p<1$![]() , and $p\neq q$
, and $p\neq q$![]() . Let $A$
. Let $A$![]() and $B$
and $B$![]() be two operators on $\ell _2^n$
be two operators on $\ell _2^n$![]() such that $(A,B)$
such that $(A,B)$![]() has $(\mathbf {I}_{q,p})$
has $(\mathbf {I}_{q,p})$![]() . If $A<0$
. If $A<0$![]() or $A> 0$
or $A> 0$![]() then
then
Proof of lemma 4.12. Let $\{d_1,d_2,\ldots,d_n\}$![]() be the complete set of eigenvalues of $A$
be the complete set of eigenvalues of $A$![]() . Note that all $d_k, 1\leq k\leq n$
. Note that all $d_k, 1\leq k\leq n$![]() are non-zero and have the same sign. Since $A$
are non-zero and have the same sign. Since $A$![]() is invertible, there exists a real number $\epsilon >0$
is invertible, there exists a real number $\epsilon >0$![]() such that $\sigma (A+tB)\cap [-\epsilon,\epsilon ]=\emptyset$
such that $\sigma (A+tB)\cap [-\epsilon,\epsilon ]=\emptyset$![]() for $t$
for $t$![]() in a small neighbourhood of $0$
in a small neighbourhood of $0$![]() . Now we define the compactly supported smooth function $f_p:\mathbb {R}\rightarrow \mathbb {C}$
. Now we define the compactly supported smooth function $f_p:\mathbb {R}\rightarrow \mathbb {C}$![]() such that $f_p(x)=|x|^p$
such that $f_p(x)=|x|^p$![]() on $[-2,-\epsilon ]\cup [\epsilon,2]$
on $[-2,-\epsilon ]\cup [\epsilon,2]$![]() . Thus, by applying theorem 4.2 corresponding to the function $f_p$
. Thus, by applying theorem 4.2 corresponding to the function $f_p$![]() we get
we get

For the last identity in (4.35), we refer to [Reference Chattopadhyay, Hong, Pal, Pradhan and Ray6, equation 4.3]. Note that $f_p^{[2]}(d_l,d_l,d_l)=p(p-1)|d_l|^{p-1}<0$![]() and for $d_l\neq d_k$
and for $d_l\neq d_k$![]() , $(f_p^{[2]}(d_l,d_k,d_k)+f_p^{[2]}(d_k,d_l,d_l))=p\cdot d_l^{p-2}\cdot \dfrac {1-\left (\frac {d_k}{d_l}\right )^{p-1}}{1-\left (\frac {d_k}{d_l}\right )}<0$
, $(f_p^{[2]}(d_l,d_k,d_k)+f_p^{[2]}(d_k,d_l,d_l))=p\cdot d_l^{p-2}\cdot \dfrac {1-\left (\frac {d_k}{d_l}\right )^{p-1}}{1-\left (\frac {d_k}{d_l}\right )}<0$ . Since $(A,B)$
. Since $(A,B)$![]() has $(\mathbf {I}_{q,p})$
has $(\mathbf {I}_{q,p})$![]() , so by corollary 4.7, we have $AB\neq 0$
, so by corollary 4.7, we have $AB\neq 0$![]() . Therefore, along the same line of argument of the proof of [Reference Chattopadhyay, Hong, Pal, Pradhan and Ray6, lemma 4.1], from (4.35), we conclude the proof.
. Therefore, along the same line of argument of the proof of [Reference Chattopadhyay, Hong, Pal, Pradhan and Ray6, lemma 4.1], from (4.35), we conclude the proof.
Note that in the above lemma 4.12, we prove that $\frac {{\rm d}^2}{{\rm d}t^2}\bigg |_{t=0}{\lVert }{A+tB}{\rVert }_p^p< 0$![]() under some conditions on $A$
under some conditions on $A$![]() and $B.$
and $B.$![]() We want to point out that these types of results are often useful in various contexts. We refer to [Reference Zhang47] where the author obtained an alternative proof of a famous theorem of [Reference Ball, Carlen and Lieb2] (see also [Reference Kosaki23, Reference Richard and Quanhua40]). To obtain this, we use theory of multiple operator integrals and operator derivatives. We refer [Reference Potapov, Skripka and Sukochev33–Reference Potapov and Sukochev35] for more on this direction.
We want to point out that these types of results are often useful in various contexts. We refer to [Reference Zhang47] where the author obtained an alternative proof of a famous theorem of [Reference Ball, Carlen and Lieb2] (see also [Reference Kosaki23, Reference Richard and Quanhua40]). To obtain this, we use theory of multiple operator integrals and operator derivatives. We refer [Reference Potapov, Skripka and Sukochev33–Reference Potapov and Sukochev35] for more on this direction.
Now we are in a position to state and prove our main theorem in this section.
Theorem 4.13 Let $0< p<1,\,2\leq q< \infty,\, 2\leq m\leq n<\infty$![]() . Then, there is no isometric embedding $T:S_q^m\to S_p^n$
. Then, there is no isometric embedding $T:S_q^m\to S_p^n$![]() with $T(\text {diag}(1,0,\ldots,0))=A,$
with $T(\text {diag}(1,0,\ldots,0))=A,$![]() and $T(\text {diag}(0,1,\ldots,0))=B$
and $T(\text {diag}(0,1,\ldots,0))=B$![]() such that
such that
• $A,B\in M_n^{sa},$

• either $A\geq 0$
 or $A\leq 0$
or $A\leq 0$ .
.
Proof. Here, we use the same notations that are used in the proof of theorem 4.8. On the contrary, suppose there exists such an isometric embedding. Then, we have identity (4.4), and consequently (4.5). Altogether, we have

If $A$![]() is invertible, then the right-hand side of (4.36) is analytic in $\Omega$
is invertible, then the right-hand side of (4.36) is analytic in $\Omega$![]() . Therefore, $\|A+tB\|_p^p$
. Therefore, $\|A+tB\|_p^p$![]() has a power series representation in $\Omega$
has a power series representation in $\Omega$![]() . Consequently, from (4.36), we have
. Consequently, from (4.36), we have

It is easy to observe that $\frac {{\rm d}}{{\rm d}t}\bigg |_{t=0}{\lVert }{A+tB}{\rVert }_p^p=0$![]() as $1\leq (1+|t|^q)^{\frac {p}{q}}={\lVert }{A+tB}{\rVert }_p^p$
as $1\leq (1+|t|^q)^{\frac {p}{q}}={\lVert }{A+tB}{\rVert }_p^p$![]() for all $t\in \Omega$
for all $t\in \Omega$![]() . Therefore, from (4.37), we have
. Therefore, from (4.37), we have
Taking limit $t\to 0$![]() on both sides of (4.38), we have
on both sides of (4.38), we have
which is impossible as $\frac {p}{q}>0$![]() . We conclude that $A$
. We conclude that $A$![]() must be a singular matrix. Then, by the similar argument as given in the proof of theorem 4.9, we can deduce identity (4.8) from identity (4.5). Thus, we have
must be a singular matrix. Then, by the similar argument as given in the proof of theorem 4.9, we can deduce identity (4.8) from identity (4.5). Thus, we have

Observe that $\Psi _{1}(0)=0$![]() . Let $\Psi _{1}(t)=t\Psi _2(t)$
. Let $\Psi _{1}(t)=t\Psi _2(t)$![]() , where $\Psi _{2}(\cdot )$
, where $\Psi _{2}(\cdot )$![]() is some analytic function in $\Omega$
is some analytic function in $\Omega$![]() . Then, from (4.39), we have,
. Then, from (4.39), we have,


As $q\geq 2$![]() , from the above equation (4.39), it follows that $m_kp\geq 2$
, from the above equation (4.39), it follows that $m_kp\geq 2$![]() for all $k\in \{1,\ldots,l\}$
for all $k\in \{1,\ldots,l\}$![]() . Let $J\subseteq \{1,\ldots,l\}$
. Let $J\subseteq \{1,\ldots,l\}$![]() be such that $m_kp=2$
be such that $m_kp=2$![]() for $k\in J$
for $k\in J$![]() . Note that $J$
. Note that $J$![]() could be empty. Then, by repeating the similar kind of arguments as given in sub-case-II of the proof of [Reference Chattopadhyay, Hong, Pal, Pradhan and Ray6, theorem 4.2], we have
could be empty. Then, by repeating the similar kind of arguments as given in sub-case-II of the proof of [Reference Chattopadhyay, Hong, Pal, Pradhan and Ray6, theorem 4.2], we have

Therefore, from (4.40), we conclude that
which leads to a contradiction. This completes the proof.
Corollary 4.14 Let $\mathcal {M}$![]() be a finite dimensional von Neumann algebra with normal semifinite faithful trace, and $\text {dim}\mathcal {M}\geq 2$
be a finite dimensional von Neumann algebra with normal semifinite faithful trace, and $\text {dim}\mathcal {M}\geq 2$![]() . Let $m\geq 2$
. Let $m\geq 2$![]() . Let $p\in (0,1)$
. Let $p\in (0,1)$![]() . Then, there is no isometric embedding of $S_q^m$
. Then, there is no isometric embedding of $S_q^m$![]() into $L_p(\mathcal {M})$
into $L_p(\mathcal {M})$![]() for $q\in (0,2)\setminus \{1\}$
for $q\in (0,2)\setminus \{1\}$![]() , $S_1^m$
, $S_1^m$![]() into $L_p(\mathcal {M})$
into $L_p(\mathcal {M})$![]() for $p\in (0,1)\setminus \{\frac {1}{k}:k\in \mathbb {N}\}$
for $p\in (0,1)\setminus \{\frac {1}{k}:k\in \mathbb {N}\}$![]() and $S_\infty ^n$
and $S_\infty ^n$![]() into $L_p(\mathcal {M})$
into $L_p(\mathcal {M})$![]() for $p\in (0,1)\setminus \{\frac {1}{k}:k\in \mathbb {N}\}.$
for $p\in (0,1)\setminus \{\frac {1}{k}:k\in \mathbb {N}\}.$![]()
Remark 4.15 The restrictions on the range of $p$![]() and $q$
and $q$![]() in the above-mentioned theorems is purely of technical nature. The main problem is that whenever we have good analyticity of both the power-series in hand, we have no more tools to compare them as the eigenvalues of the analytic family $t\mapsto A+tB$
in the above-mentioned theorems is purely of technical nature. The main problem is that whenever we have good analyticity of both the power-series in hand, we have no more tools to compare them as the eigenvalues of the analytic family $t\mapsto A+tB$![]() are in an abstract form if we use the Kato–Rellich theorem. Therefore, one needs some new ideas to solve question 1.1 for the remaining cases.
are in an abstract form if we use the Kato–Rellich theorem. Therefore, one needs some new ideas to solve question 1.1 for the remaining cases.
Acknowledgements
A. C. acknowledges the financial support provided by Mathematical Research Impact Centric Support (MATRICS) grant, File no: MTR/2019/000640, by the Science and Engineering Research Board (SERB), Department of Science and Technology (DST), Government of India. G. H. acknowledges the financial support provided by NSF of China (No. 12071355) and the Fundamental Research Funds for the Central Universities (No. 2042022kf1185). C. P. thanks the Indian Institute of Technology Guwahati, Government of India, for the financial support. S. K. R. acknowledges the financial support provided by DST-INSPIRE Faculty Fellowship No. DST/INSPIRE/04/2020/001132.