Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kovačec, Alexander
1989.
A bruhat order for bipartite graphs whose node sets are posets: Lifting, switching, and adding edges.
Order,
Vol. 6,
Issue. 3,
p.
245.
Mitrinović, D. S.
Pečarić, J. E.
and
Fink, A. M.
1991.
Inequalities Involving Functions and Their Integrals and Derivatives.
p.
285.
1992.
Convex Functions, Partial Orderings, and Statistical Applications.
Vol. 187,
Issue. ,
p.
419.
Mitrinović, D. S.
Pečarić, J. E.
and
Fink, A. M.
1993.
Classical and New Inequalities in Analysis.
p.
333.


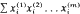 under arbitrary rearrangements of the entries of increasing
under arbitrary rearrangements of the entries of increasing 