Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T04:29:46.251Z Has data issue: false hasContentIssue false
  • English
  • Français

On quotient modules of H2(𝔻n): essential normality and boundary representations

Part of: General theory of linear operators Selfadjoint operator algebras Linear spaces and algebras of operators

Published online by Cambridge University Press:  31 January 2019

B. Krishna Das ,
Sushil Gorai  and
Jaydeb Sarkar
B. Krishna Das
Affiliation:
Department of Mathematics, Indian Institute of Technology Bombay, Powai, Mumbai, India400076 (dasb@math.iitb.ac.in; bata436@gmail.com)
Sushil Gorai
Affiliation:
Department of Mathematics and Statistics, Indian Institute of Science Education and Research Kolkata, Mohanpur 741 246, West Bengal, India (sushil.gorai@iiserkol.ac.in)
Jaydeb Sarkar
Affiliation:
Indian Statistical Institute, Statistics and Mathematics Unit, 8th Mile, Mysore Road, Bangalore560059, India (jay@isibang.ac.in; jaydeb@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 𝔻n be the open unit polydisc in ℂn, 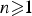$n \ges 1$, and let H2(𝔻n) be the Hardy space over 𝔻n. For 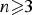$n\ges 3$, we show that if θ ∈ H∞(𝔻n) is an inner function, then the n-tuple of commuting operators $(C_{z_1}, \ldots , C_{z_n})$ on the Beurling type quotient module 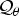${\cal Q}_{\theta }$ is not essentially normal, where

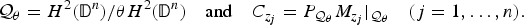$${\rm {\cal Q}}_\theta = H^2({\rm {\open D}}^n)/\theta H^2({\rm {\open D}}^n)\quad {\rm and}\quad C_{z_j} = P_{{\rm {\cal Q}}_\theta }M_{z_j}\vert_{{\rm {\cal Q}}_\theta }\quad (j = 1, \ldots ,n).$$
Rudin's quotient modules of H2(𝔻2) are also shown to be not essentially normal. We prove several results concerning boundary representations of C*-algebras corresponding to different classes of quotient modules including doubly commuting quotient modules and homogeneous quotient modules.

Keywords

Hardy spacereproducing kernel Hilbert spacesquotient modulesessential normalityboundary representations

MSC classification

Primary: 47A13: Several-variable operator theory (spectral, Fredholm, etc.)
Secondary: 47A20: Dilations, extensions, compressions 47L25: Operator spaces (= matricially normed spaces) 47L40: Limit algebras, subalgebras of $C^*$-algebras 46L05: General theory of $C^*$-algebras 46L06: Tensor products of $C^*$-algebras
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 3 , June 2020 , pp. 1339 - 1359
Copyright
Copyright © 2019 The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Arveson, W.. Subalgebras of C*-algebras. Acta Math. 123 (1969), 141–224.CrossRefGoogle Scholar
2Arveson, W.. Subalgebras of C*-algebras II. Acta Math. 128 (1972), 271–308.CrossRefGoogle Scholar
3Arveson, W.. Quotients of standard Hilbert modules. Trans. Amer. Math. Soc. 359 (2007), 6027–6055.CrossRefGoogle Scholar
4Brown, L., Douglas, R. and Fillmore, P.. Extension of C*-algebras and K-homology. Ann. Math. 105 (1977), 265–324.CrossRefGoogle Scholar
5Chattopadhyay, A., Das, B. K. and Sarkar, J.. Star-generating vectors of Rudin's quotient modules. J. Funct. Anal. 267 (2014), 4341–4360.CrossRefGoogle Scholar
6Chattopadhyay, A., Das, B. K. and Sarkar, J.. Tensor product of quotient Hilbert modules. J. Math. Anal. Appl. 429 (2015), 727–747.CrossRefGoogle Scholar
7Chen, X. and Guo, K.. Analytic Hilbert modules. π-Chapman & Hall/CRC Res. Notes Math. 433 (2003.Google Scholar
8Clark, D.. Restrictions of H p functions in the polydisk. Amer. J. Math. 110 (1988), 1119–1152.CrossRefGoogle Scholar
9Das, B. K. and Sarkar, J.. Rudin's Submodules of H 2(𝔻2). C. R. Acad. Sci. Paris 353 (2015), 51–55.CrossRefGoogle Scholar
10Davidson, K. and Kennedy, M.. The Choquet boundary of an operator system. Duke Math. J. 164 (2015), 2989–3004.CrossRefGoogle Scholar
11Douglas, R. G. and Paulsen, V. I.. Hilbert modules over function algebras, Research Notes in Mathematics Series, 47 (Harlow: Longman, 1989).Google Scholar
12Guo, K. and Wang, P.. Essentially normal Hilbert modules and K-homology III: homogeneous quotient modules on the bidisk. Sci. China Ser. A 50 (2007), 387–411.CrossRefGoogle Scholar
13Guo, K. and Wang, K.. Essentially normal Hilbert modules and K-homology. Math. Ann. 340 (2008), 907–934.CrossRefGoogle Scholar
14Guo, K. and Wang, K.. Beurling type quotient modules over the bidisk and boundary representations. J. Funct. Anal. 257 (2009), 3218–3238.CrossRefGoogle Scholar
15He, W.. Boundary representations on co-invariant subspaces of Bergman space. Proc. Amer. Math. Soc. 138 (2010), 615–622.CrossRefGoogle Scholar
16Hopenwasser, A.. Boundary representations and tensor products of C*-algebras. Proc. Amer. Math. Soc. 71 (1978), 95–98.Google Scholar
17Izuchi, K., Nakazi, T. and Seto, M.. Backward shift invariant subspaces in the bidisc II. J. Oper. Theory 51 (2004), 361–376.Google Scholar
18Rudin, W.. Function theory in polydiscs (New York: Benjamin, 1969).Google Scholar
19Sarkar, J.. Jordan blocks of H 2(𝔻n). J. Oper. Theory 72 (2014), 371–385.CrossRefGoogle Scholar
20Sarkar, J., Sasane, A. and Wick, B.. Doubly commuting submodules of the Hardy module over polydiscs. Stud. Math. 217 (2013), 179–192.CrossRefGoogle Scholar
21Wang, P.. The essential normality of -type quotient module of Hardy module on the polydisc. Proc. Amer. Math. Soc. 142 (2014), 151–156.CrossRefGoogle Scholar
22Zhu, K.. Restriction of the Bergman shift to an invariant subspace. Quart. J. Math. Oxford Ser. (2) 48 (1997), 519–532.CrossRefGoogle Scholar