Published online by Cambridge University Press: 14 November 2011
A class of singular real formally self-adjoint differential expressions M on I = [a, = ∞) (a ∈ ℝ), i.e. expressions of the form My = 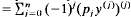 with pj ≧ 0 (j = 0, …, n – 1), pn > 0 is constructed with the following property: For every integer k with 0 ≦ k < n/2 there exists an expression M in this class such that the deficiency index of T0(M) – the minimal operator associated with M – is n + 2k. This generalises a result in [3] and proves part of the McLeod's conjecture.
with pj ≧ 0 (j = 0, …, n – 1), pn > 0 is constructed with the following property: For every integer k with 0 ≦ k < n/2 there exists an expression M in this class such that the deficiency index of T0(M) – the minimal operator associated with M – is n + 2k. This generalises a result in [3] and proves part of the McLeod's conjecture.