Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T15:00:03.184Z Has data issue: false hasContentIssue false
  • English
  • Français

On strongly decreasing solutions of cyclic systems of second-order nonlinear differential equations

Part of: Real functions Qualitative theory

Published online by Cambridge University Press:  02 September 2015

Jaroslav Jaroš  and
Kusano Takaŝi
Jaroslav Jaroš
Affiliation:
Department of Mathematical Analysis and Numerical Mathematics, Faculty of Mathematics, Physics and Informatics, Comenius University, 842 48 Bratislava, Slovakia (jaros@fmph.uniba.sk)
Kusano Takaŝi
Affiliation:
Department of Mathematics, Faculty of Science, Hiroshima University, Higashi Hiroshima 739-8526, Japan (kusanot@zj8.so-net.ne.jp)
Get access Rights & Permissions [Opens in a new window]

Abstract

The n-dimensional cyclic system of second-order nonlinear differential equations

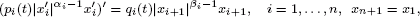
is analysed in the framework of regular variation. Under the assumption that αi and βi are positive constants such that α1 … αn > β1 … βn and pi and qi are regularly varying functions, it is shown that the situation in which the system possesses decreasing regularly varying solutions of negative indices can be completely characterized, and moreover that the asymptotic behaviour of such solutions is governed by a unique formula describing their order of decay precisely. Examples are presented to demonstrate that the main results for the system can be applied effectively to some classes of partial differential equations with radial symmetry to provide new accurate information about the existence and the asymptotic behaviour of their radial positive strongly decreasing solutions.

Keywords

systems of differential equationspositive solutionsasymptotic behaviourregularly varying functions

MSC classification

Primary: 34C11: Growth, boundedness
Secondary: 26A12: Rate of growth of functions, orders of infinity, slowly varying functions
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 145 , Issue 5 , October 2015 , pp. 1007 - 1028
Copyright
Copyright © Royal Society of Edinburgh 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)