Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-14T22:35:29.759Z Has data issue: false hasContentIssue false
  • English
  • Français

On the algebra of a free monoid

Published online by Cambridge University Press:  14 November 2011

M. J. Crabb ,
C. M. McGregor ,
W. D. Munn  and
S. Wassermann
M. J. Crabb
Affiliation:
Department of Mathematics, University of Glasgow, Glasgow G12 8QW, Scotland, U.K.
C. M. McGregor
Affiliation:
Department of Mathematics, University of Glasgow, Glasgow G12 8QW, Scotland, U.K.
W. D. Munn
Affiliation:
Department of Mathematics, University of Glasgow, Glasgow G12 8QW, Scotland, U.K.
S. Wassermann
Affiliation:
Department of Mathematics, University of Glasgow, Glasgow G12 8QW, Scotland, U.K.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 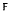denote a subring of the complex field that contains 1 and is closed under complex conjugation. It is shown that, with respect to the involution induced by word-reversal, the algebra over 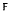of a free monoid admits a trace and a separating family of star matrix representations. From the existence of a trace it is deduced that the aforementioned involution is special, in the sense of Easdown and Munn. Similar results hold for the algebra over 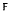of a free monoid with involution.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 126 , Issue 5 , 1996 , pp. 939 - 945
Copyright
Copyright © Royal Society of Edinburgh 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Barnes, B. A. and Duncan, J.. The Banach algebra l 1(S). J. of Fund. Anal. 18 (1975), 96–113.CrossRefGoogle Scholar
2Cohn, P. M.. Free rings and their relations (London: Academic Press, 1971).Google Scholar
3Crabb, M. J. and Munn, W. D.. Trace functions on the algebras of certain E-unitary inverse semigroups. Proc. Roy. Soc. Edinburgh Sect. A 125 (1995), 1077–1084.CrossRefGoogle Scholar
4Easdown, D. and Munn, W. D.. On semigroups with involution. Bull. Austral. Math. Soc. 48 (1993), 93–100.CrossRefGoogle Scholar
5Easdown, D. and Munn, W. D.. Trace functions on inverse semigroup algebras. Bull. Austral. Math. Soc. 52 (1995), 359–372.CrossRefGoogle Scholar
6Goodearl, K. R. and Menal, P.. Free and residually finite-dimensional C*-algebras. J. of Fund. Anal. 90 (1990), 391–410.CrossRefGoogle Scholar
7Passman, D. S.. The algebraic theory of group rings (New York: Wiley-Interscience, 1977).Google Scholar
8Petrich, M.. Inverse semigroups (New York: Wiley-Interscience, 1984).Google Scholar