Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T11:16:11.591Z Has data issue: false hasContentIssue false
  • English
  • Français

On the completeness of eigenvectors of right definite multiparameter problems

Published online by Cambridge University Press:  14 November 2011

Hans Volkmer
Hans Volkmer
Affiliation:
FB 6-Mathematik, Universität Essen GHS, Universitätsstr. 3, D-4300 Essen 1, BRD
Get access Rights & Permissions [Opens in a new window]

Synopsis

We prove that there exists a complete system of eigenvectors of the eigenvalue problem

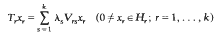
for self-adjoint operators Tr and Vrs on separable Hilbert spaces Hr. It is assumed that

(i) the operators Tr have discrete spectrum;

(ii) the operators Vrs are bounded and commute for each r;

(iii) the operators Vrs have the definite sign factor property.

This theorem generalizes and improves a result of Cordes for two-parameter problems. The proof of the theorem depends on an approximation of the given eigenvalue problem by simpler problems, a technique which is related to Atkinson's proof of his expansion theorem.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 96 , Issue 1-2 , 1984 , pp. 69 - 78
Copyright
Copyright © Royal Society of Edinburgh 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Atkinson, F. V.. Multiparameter Eigenvalue Problems, Vol. 1 (New York: Academic Press, 1972).Google Scholar
2Binding, P. A.. Multiparameter definiteness conditions II. Proc. Roy. Soc. Edinburgh Sect. A 93 (1982), 47–61.CrossRefGoogle Scholar
3Binding, P. A. and Browne, P. J.. Positivity results for determinantal operators. Proc. Roy. Soc. Edinburgh Sect. A 81 (1978), 267–271.CrossRefGoogle Scholar
4Binding, P. A., Kallstrom, A. and Sleeman, B. D.. An abstract multiparameter spectral theory. Proc. Roy. Soc. Edinburgh Sect. A 92 (1982), 193–204.Google Scholar
5Browne, P. J.. Abstract multiparameter theory I. J. Math. Anal. Appl. 60 (1977), 259–273.Google Scholar
6Cordes, H. O.. Der Entwicklungssatz nach Produkten bei singularen Eigenwertproblemen partieller Differentialgleichungen, die durch Separation zerfallen. Nachr. Akad. Wiss. Gottingen 1954, 51–69.Google Scholar
7Rellich, F.. Storungstheorie der Spektralzerlegung V. Math. Ann. 118 (1941/1943), 462–484.Google Scholar
8Volkmer, H.. On multiparameter theory. J. Math. Anal. Appl. 86 (1982), 44–53.Google Scholar