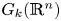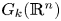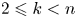On the topological complexity and zero-divisor cup-length of real Grassmannians

Abstract

Topological complexity naturally appears in the motion planning in robotics. In this paper we consider the problem of finding topological complexity of real Grassmann manifolds $G_k(\mathbb {R}^{n})$. We use cohomology methods to give estimates on the zero-divisor cup-length of $G_k(\mathbb {R}^{n})$ for various $2\leqslant k< n$, which in turn give us lower bounds on topological complexity. Our results correct and improve several results from Pavešić (Proc. Roy. Soc. Edinb. A 151 (2021), 2013–2029).

1. Introduction

For a path-connected space $X$ we denote its topological complexity by $\mathrm {TC}(X)$. In [9] the author considered the problem of finding $\mathrm {TC}(G_k(\mathbb {R}^{n}))$ for various $2\leqslant k< n$ (in this paper, $G_k(\mathbb {R}^{n})$ denotes the real Grassmann manifold of $k$-dimensional subspaces in $\mathbb {R}^{n}$). Unfortunately, there is a problem with the proof of the main lemma of that paper (lemma 4.4) and the consequential results on the topological complexity (theorems 4.5, 4.8 and 4.12); see [10]. In this paper we reconsider this problem, and as an outcome correct and improve several results from [9]. As in [9], we use the cohomology method to obtain our results.

This paper closely follows and builds on the ideas presented in [9] (so, for background, motivation and all undefined notions, the reader is advised to consult [9]). Throughout the paper we will use, as much as possible, the notation from [9]. In particular, we will be working with the unreduced topological complexity, as defined by Farber in [5] (e.g. by this definition the topological complexity of a contractible space is equal to 1).

The paper is organized as follows. In § 2 we describe the cohomology method mentioned above and give an overview of the cohomology of real Grassmannians. In § 3 we consider the case $k=2$. We obtain the exact value of the zero-divisor cup-length of $G_2(\mathbb {R}^{2^{s}+1})$ (denoted by $\mathrm {zcl}(G_2(\mathbb {R}^{2^{s}+1}))$, and defined in § 2) for $s\geqslant 2$; additionally, for $s\geqslant 3$, $2^{s}+4\leqslant n\leqslant 2^{s+1}$ we prove a lower bound for $\mathrm {zcl}(G_2(\mathbb {R}^{n}))$. These results show that the value of the zero-divisor cup-length given in [9, theorem 4.5] is not correct; what is more interesting, our results improve lower bounds for topological complexity stated in the same theorem. Section 4 is devoted to the case $k=3$. Separately, we prove lower bounds for $\mathrm {zcl}(G_3(\mathbb {R}^{n}))$ in the cases $n=2^{s}+1$ (for $s\geqslant 3$), and $2^{s}+3\leqslant n\leqslant 2^{s+1}$ (for $s\geqslant 2$). The first result shows that the corresponding result from [9, theorem 4.8] is not correct, and improves the stated lower bound for topological complexity of $G_3(\mathbb {R}^{2^{s}+1})$ (for $s\geqslant 5$). In § 5 we give a general lower bound for $\mathrm {zcl}(G_k(\mathbb {R}^{n}))$ (for $k\geqslant 4$). For $k\geqslant 9$ this result improves the bounds stated in [9, theorem 4.10].

2. Background and notation

As mentioned in the Introduction, to obtain our results we use the so-called cohomology method, which we now (briefly) explain.

Let $\Delta :X\rightarrow X\times X$ denote the diagonal map. Then the elements of

\[ \mathrm{Ker}(\Delta^{*}:H^{*}(X\times X;\mathbb{Z}_2)\rightarrow H^{*}(X;\mathbb{Z}_2)) \]

are called zero-divisors. Furthermore, the zero-divisor cup-length of $X$, denoted by $\mathrm {zcl}(X)$, is defined to be the maximum number of elements from $\mathrm {Ker}\,\Delta ^{*}$ whose product is non-zero. In [5], Farber proved that $\mathrm {zcl}(X)$ gives a lower bound for $\mathrm {TC}(X)$, that is $\mathrm {TC}(X)\geqslant \mathrm {zcl}(X)+1$. Hence, a lower bound for $\mathrm {zcl}(X)$ immediately gives a lower bound for $\mathrm {TC}(X)$. Note that for every $w\in H^{*}(X;\mathbb {Z}_2)$ the element

\[ z(w)=w\otimes 1+1\otimes w\in H^{*}(X\times X;\mathbb{Z}_2) \]

is in $\mathrm {Ker}\,\Delta ^{*}$ (since $\Delta ^{*}(z(w))=w\cdot 1+1\cdot w=0$). Then, by [2, lemma 5.2], $\mathrm {Ker}\,\Delta ^{*}$ is generated as an ideal by these elements, that is by the set $\{z(w)\,:\,w\in H^{*}(X;\mathbb {Z}_2)\}$. So, if $\mathrm {zcl}(X)=t$, then there are classes $x_1,\,x_2,\,\ldots,\,x_t\in {H}^{*}(X;\mathbb {Z}_2)$ such that $z(x_1)z(x_2)\cdots z(x_t)\neq 0$.

To get the best possible results on $\mathrm {TC}(G_k(\mathbb {R}^{n}))$ using the cohomology method, one requires fine understanding of the cohomology algebra $H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$. There are several ways to describe this algebra; in this paper we will use the one due to Borel (see [1]):

\[ H^{*}(G_k(\mathbb{R}^{n});\mathbb{Z}_2)\cong \mathbb{Z}_2[w_1,w_2,\ldots,w_k]/I_{k,n}, \]

where $w_1,\,w_2,\,\ldots,\,w_k$ are the Stiefel–Whitney classes of the canonical $k$-dimensional vector bundle over $G_k(\mathbb {R}^{n})$, and $I_{k,n}=(\overline {w}_{n-k+1},\,\overline {w}_{n-k+2},\,\ldots,\,\overline {w}_{n})$ is the ideal generated by dual classes.

Although Borel's description of $H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$ appears simple enough, it turns out that performing concrete calculations in this algebra can be rather difficult. Hence, one usually needs to apply some additional methods and properties of $H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$. The following result gives an additive basis for this algebra (see, e.g. [7, 11]).

Proposition 2.1 The set $B_{k,n-k}=\{w_1^{a_1}\cdots w_k^{a_k}\,:\,0\leqslant a_1+\cdots +a_k\leqslant n-k\}$ is an additive basis for $H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$.

The height of a class $c\in \widetilde {H}^{*}(X;\mathbb {Z}_2)$, denoted by $\mathrm {ht}(c)$, is the largest $m\in \mathbb {N}$ such that $c^{m}\neq 0$. For $k\geqslant 2$, the height of $w_1\in H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$ is obtained by Stong in [12]: if $2\leqslant k\leqslant n-k$ and $s$ is the unique positive integer such that $2^{s}< n\leqslant 2^{s+1}$, then

(2.1)\begin{equation} \mathrm{ht}(w_1)=\left\{\begin{array}{@{}rl} 2^{s+1}-2, & \mbox{if }k=2\mbox{ or }(k,n)=(3,2^{s}+1), \\ 2^{s+1}-1, & \mbox{otherwise}. \end{array}\right. \end{equation}

In this paper we will often use Stong's method from [12] for calculations in $H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$ (later this method was generalized by Korbaš and Lörinc to all flag manifolds, see [8]). In what follows we briefly explain this method.

Let $\mathrm {Flag}(\mathbb {R}^{n})$ denote the (real) complete flag manifold ($n\geqslant 2$). Denote by $e_i:=w_1(\gamma _i)$ the first Stiefel–Whitney class of the canonical line bundle $\gamma _i$ over $\mathrm {Flag}(\mathbb {R}^{n})$, for $1\leqslant i\leqslant n$. Then we have the map $\pi :\mathrm {Flag}(\mathbb {R}^{n})\rightarrow G_k(\mathbb {R}^{n})$, given by

\[ \pi(S_1,\ldots,S_{k},S_{k+1},\ldots,S_n)=(S_1\oplus\cdots\oplus S_{k},S_{k+1}\oplus\cdots\oplus S_n). \]

The following result will be very useful for our calculations in $H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$ (and $H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$).

Proposition 2.2

1. (1) The set $B_n=\{e_1^{a_1}e_2^{a_2}\cdots e_{n-1}^{a_{n-1}}\,:\,0\leqslant a_i\leqslant n-i\}$ is an additive basis for $H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$.

2. (2) $\mathrm {ht}(e_i)=n-1$ for $1\leqslant i\leqslant n$. In particular $e_i^{n}=0$ for $1\leqslant i\leqslant n$.

3. (3) A monomial $e_1^{a_1}e_2^{a_2}\cdots e_n^{a_n}\in H^{\binom {n}{2}}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$ is non-zero if and only if $(a_1,\,a_2,\,\ldots,\,a_n)$ is a permutation of the $n$-tuple $(n-1,\,n-2,\,\ldots,\,1,\,0)$.

4. (4) If $u\in H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$ and

   \[ v=e_1^{k-1}e_2^{k-2}\cdots e_{k-1}\cdot e_{k+1}^{n-k-1}e_{k+2}^{n-k-2}\cdots e_{n-1}\in H^{*}(\mathrm{Flag}(\mathbb{R}^{n});\mathbb{Z}_2), \]
   then $\pi ^{*}(u)\cdot v\in H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$, and $u\neq 0$ if and only if $\pi ^{*}(u)\cdot v\neq 0$.

5. (5) For $1\leqslant i\leqslant k,$ $\pi ^{*}(w_{i})$ is the $i$-th elementary symmetric polynomial in the variables $e_{1},\,e_{2},\,\ldots,\,e_{k}$.

Heights of the classes $z(w_1)$ and $z(w_k)$ will be very useful in our calculations. In what follows we determine these values.

It turns out that if $\mathrm {ht}(w)$ is known, then $\mathrm {ht}(z(w))$ can easily be calculated. This is proven in lemma 4.3 from [9]. Namely, one has: if $w\in H^{*}(X;\mathbb {Z}_2)$ and $t$ is the unique non-negative integer such that $2^{t}\leqslant \mathrm {ht}(w)<2^{t+1}$, then

(2.2)\begin{equation} \mathrm{ht}(z(w))=2^{t+1}-1. \end{equation}

We will apply this identity for $X=G_k(\mathbb {R}^{n})$, when $2\leqslant k\leqslant n-k$. If $2^{s}< n\leqslant 2^{s+1}$, then (2.1) implies

(2.3)\begin{equation} \mathrm{ht}(z(w_1))=2^{s+1}-1. \end{equation}

On the other hand, proposition 2.1 implies $w_k^{n-k}\neq 0$, so $\mathrm {ht}(w_k)=n-k$ (by observing dimension we conclude that $w_k^{n-k+1}=0$). Hence, if $t$ is the unique non-negative integer such that $2^{t}\leqslant n-k<2^{t+1}$, then (2.2) implies

(2.4)\begin{equation} \mathrm{ht}(z(w_k))=2^{t+1}-1. \end{equation}

The following lemma will be particularly useful in § 3.

Lemma 2.3 Let $m,\,k,\,n\in \mathbb {N},$ $k< n,$ and $d_1,\,\ldots,\,d_m\in \mathbb {N}$ be such that $d_1+\cdots +d_m\geqslant 2k(n-k)$. If $x_i\in H^{d_i}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$ for $1\leqslant i\leqslant m,$ then

\[ z(x_1)\cdots z(x_m)=0. \]

Proof. Note that the product $p=z(x_1)\cdots z(x_m)$ is the sum of certain classes of the form $x\otimes y+y\otimes x$, for some $x,\,y\in H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$. Since $p$ is in dimension at least $2k(n-k)=2\dim G_k(\mathbb {R}^{n})$, so is $x\otimes y$, and hence $x,\,y\in H^{k(n-k)}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$ or $x\otimes y=y\otimes x=0$. There is only one non-zero class in $H^{k(n-k)}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$, namely $w_k^{n-k}$ (by proposition 2.1), and hence $x\otimes y=y\otimes x=0$ or $x\otimes y=w_k^{n-k}\otimes w_k^{n-k}=y\otimes x$. In both cases $x\otimes y+y\otimes x=0$, which implies $p=0$.

Also, we recall some results from [9] that will be used in our calculations.

Lemma 2.4

1. (a) If $2^{s}< n\leqslant 2^{s+1},$ then $w_1^{2^{s}} w_2^{n-2^{s}-1}\,{\neq}\,0$ and $w_1^{2^{s}}w_2^{n-2^{s}}\,{=}\,0$ in $H^{*}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$.

2. (b) If $2^{s}+3\leqslant n\leqslant 2^{s+1}$ and $t\,{=}\,n-2^{s},$ then $w_1^{2^{s}} w_2^{2^{s}}w_3^{t-3}\,{\neq}\, 0$ in $H^{*}(G_3(\mathbb {R}^{n});\mathbb {Z}_2)$.

Throughout the paper we use the same notation as in this section.

Finally, let us say a few words on lemma 4.4 from [9] and our strategy that bypasses the application of this lemma. In lemma 4.4 from [9] the author assumes that $u_1,\,\ldots,\,u_n\in H^{*}(X;\mathbb {Z}_2)$ and $k_1,\,\ldots,\,k_n\in \mathbb {N}$ are such that $u_1^{k_1}\cdots u_n^{k_n}\neq 0$, and wants to prove that $A=z(u_1)^{2^{r_1}-1}\cdots z(u_n)^{2^{r_n}-1}\neq 0$, where $r_i$ is the unique integer such that $2^{r_i-1}\leqslant k_i<2^{r_i}$ for $1\leqslant i\leqslant n$. For this he notices that after expanding $A$ one summand is $u_1^{k_1}\cdots u_n^{k_n}\otimes u_1^{2^{r_1}-k_1-1}\cdots u_n^{2^{r_n}-k_n-1}$, which is nonzero, and from this immediately concludes that $A\neq 0$. As we will see in the proofs of our results, the problem is that the set

\[ S=\{(l_1,\ldots,l_n)\,:\,0\leqslant l_i\leqslant 2^{r_i}-1,\, u_1^{l_1}\cdots u_n^{l_n}=u_1^{k_1}\cdots u_n^{k_n}\} \]

can contain more than one element, and hence that the corresponding summands of $A$ with the first coordinate equal to $u_1^{k_1}\cdots u_n^{k_n}$ may cancel out. So, in our proofs we choose the $n$-tuple $(k_1,\,\ldots,\,k_n)$ a bit more carefully to ensure that

\[ \sum_{(l_1,\ldots,l_n)\in S}u_1^{2^{r_1}-l_1-1}\cdots u_n^{2^{r_n}-l_n-1}\neq 0 \]

and that this further leads to $A\neq 0$ (note: in our applications the degree of $z(u_i)$ in $A$ will not always be $2^{r_i}-1$, so we will have slightly different formulas than the one given above).

3. Zero-divisor cup-length of $G_2(\mathbb {R}^{n})$

Let $s$ be the unique integer such that $2^{s}< n\leqslant 2^{s+1}$. In this section we consider $\mathrm {zcl}(G_2(\mathbb {R}^{n}))$. We note that propositions 3.7 and 3.10, that we prove in this section, show that the corresponding results of [9, theorem 4.5] are not correct (see also remark 3.9). Fortunately, correct versions give better lower bounds for the topological complexity of $G_2(\mathbb {R}^{n})$.

We will compare our results with the following upper bound from [9] (this result is a consequence of a general result from [3, theorem 1]).

Proposition 3.1 If $1\leqslant k< n,$ then $\mathrm {TC}(G_k(\mathbb {R}^{n}))\leqslant 2k(n-k)$. In fact, if $k\neq 1$ and $(k,\,n)\neq (2,\,2^{d}+1)$ for all $d\in \mathbb {N},$ then $\mathrm {TC}(G_k(\mathbb {R}^{n}))\leqslant 2k(n-k)-1$.

3.1 Preliminary lemmas

Let $n$ be a positive integer and $n=\sum _{i=0}^{t}\alpha _i\cdot 2^{i}$, where $\alpha _i\in \{0,\,1\}$ for $0\leqslant i\leqslant t$ and $\alpha _t=1$, its representation in base 2. Then we write $n:=(\alpha _t,\,\ldots,\,\alpha _1,\,\alpha _0)_2$.

As we use $\mathbb {Z}_2$ coefficient the following special case of Lucas’ theorem will be particularly useful to us: if $n:=(\alpha _t,\,\ldots,\,\alpha _1,\,\alpha _0)_2$ and $m:=(\beta _r,\,\ldots,\,\beta _1,\,\beta _0)_2$, then

\[ \binom{n}{m}\equiv 1\pmod 2\qquad \mbox{if and only if}\qquad t\geqslant r\quad\mbox{and}\quad\alpha_i\geqslant \beta_i\mbox{ for }0\leqslant i\leqslant r. \]

We will use the following two consequences of Lucas’ theorem throughout the paper. Let $w\in H^{*}(X;\mathbb {Z}_2)$. By Lucas’ theorem, $\binom {2^{m}}{i}$ is even for $1\leqslant i\leqslant 2^{m}-1$, and so

\[ z(w)^{2^{m}}=(w\otimes 1+1\otimes w)^{2^{m}}=w^{2^{m}}\otimes 1+1\otimes w^{2^{m}}. \]

On the other hand, by Lucas’ theorem $\binom {2^{m}-1}{i}$ is odd for all $0\leqslant i\leqslant 2^{m}-1$, and hence

\[ z(w)^{2^{m}-1}=(w\otimes 1+1\otimes w)^{2^{m}-1}=\sum_{i=0}^{2^{m}-1}w^{i}\otimes w^{2^{m}-1-i}. \]

We will also need the following result.

Lemma 3.2 Let $n$ be a non-negative integer. Then:

1. (a) $\binom {2n}{n}$ is odd if and only if $n=0;$

2. (b) $\binom {2n}{n+1}$ is odd if and only if $n=2^{t+1}-1$ for some $t\in \mathbb {N}_0$.

Proof. Part (a) immediately follows from Lucas’ theorem.

For part (b) we note that $C_n=\binom {2n}{n}-\binom {2n}{n+1}$ is the $n$-th Catalan number. Then the result follows from part (a) and the fact that $C_n$ (for $n\geqslant 1$) is odd if and only if $n=2^{t+1}-1$ for some $t\in \mathbb {N}_0$ (see [4]).

Lemma 3.3 Let $0\leqslant m\leqslant n-2$ and $\alpha _0,\,\alpha _1,\,\ldots,\,\alpha _{n-1-m}\in \mathbb {Z}_2$. Then:

1. (a) $\sum _{i=0}^{n-1-m} \alpha _ie_1^{m+i}e_2^{n-1-i}=0$ in $H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$ iff $\alpha _0=\alpha _1=\dots =\alpha _{n-1-m}$;

2. (b) for a polynomial $p\in H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$ in classes $e_1$ and $e_2$ one has

   \[ p\cdot e_3^{n-3}e_4^{n-4}\cdots e_{n-1}=0\quad{in}\quad H^{*}(\mathrm{Flag}(\mathbb{R}^{n});\mathbb{Z}_2) \]
   if and only if $p=0$ in $H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$.

Proof.

1. (a) By proposition 2.1 from [6] we have $e_2^{n-1}=e_1^{n-1}+e_1^{n-2}e_2+\dots +e_1e_2^{n-2}$ (we use this proposition for $m=1$, $k=n-1$ and $i=n-2$). Since $e_1^{n}=0$ (by proposition 2.2(2)), we have

   \[ \sum_{i=0}^{n-1-m} \alpha_ie_1^{m+i}e_2^{n-1-i}=\sum_{i=1}^{n-1-m}(\alpha_i+\alpha_0)e_1^{m+i}e_2^{n-1-i}. \]
   Since $e_1^{m+1}e_2^{n-2},\,e_1^{m+2}e_2^{n-3},\,\ldots,\,e_1^{n-1}e_2^{m}$ are in the additive basis $B_n$ (from proposition 2.2(1)), the last sum is zero if and only if $\alpha _1+\alpha _0=\alpha _2+\alpha _0=\dots =\alpha _{n-1-m}+\alpha _0=0$, i.e. if and only if $\alpha _0=\alpha _1=\dots =\alpha _{n-1-m}$.

2. (b) As in part (a) we use the identities $e_2^{n-1}=e_1^{n-1}+e_1^{n-2}e_2+\dots +e_1e_2^{n-2}$ and $e_1^{n}=e_2^{n}=0$ to express $p$ in the form $\sum \alpha _{i,j}e_1^{i}e_2^{j}$, where $\alpha _{i,j}\in \{0,\,1\}$, $0\leqslant i\leqslant n-1$ and $0\leqslant j\leqslant n-2$. Then $\sum \alpha _{i,j}e_1^{i}e_2^{j}e_3^{n-3}e_4^{n-4}\cdots e_{n-1}$ ($=pe_3^{n-3}e_4^{n-4}\cdots e_{n-1}$) is a sum of the elements from the basis $B_n$ from proposition 2.2(1); so this sum is zero if and only if $\alpha _{ij}=0$ for all $i,\,j$, i.e. if and only if $p=0$ (since $p$ is also represented in the basis $B_{n}$).

Remark 3.4 We will use the following consequence of part a) of this lemma. Let $p=\sum _{i=0}^{b-a} \alpha _ie_1^{a+i}e_2^{b-i}\in H^{a+b}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$ for some $0\leqslant a\leqslant n-2$, $a\leqslant b\leqslant n-1$. If there exist $0\leqslant i'\neq i''\leqslant b-a$ such that $\alpha _{i'}=0$ and $\alpha _{i''}=1$, then $p\neq 0$.

Furthermore, if $q\in H^{c}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$, where $c\leqslant 2n-3$, is written as a sum of some monomials of the form $e_1^{i}e_2^{j}$, then after removing all summands with $i\geqslant n$ or $j\geqslant n$ (since they are 0 by proposition 2.2(2)), we get that $q$ is written in the same way as $p$ above.

Lemma 3.5 If $2^{s}< n\leqslant 2^{s+1}$ and $a,\,b\in \mathbb {N}_0$ are such that $a+2b=2(n-2),$ then $w_1^{a}w_2^{b}\neq 0$ in $H^{2n-4}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$ if and only if

\[ (a,b)=(2^{l+1}-2,n-2^{l}-1)\quad\mbox{for some }0\leqslant l\leqslant s. \]

Proof. By proposition 2.2(4), $w_1^{a}w_2^{b}\neq 0$ in $H^{2n-4}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$ if and only if

\[ \pi^{*}(w_1^{a}w_2^{b})e_1e_3^{n-3}\cdots e_{n-1}=(e_1+e_2)^{a}(e_1e_2)^{b}e_1e_3^{n-3}\cdots e_{n-1}\neq 0 \]

in $H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$. After expanding we have

\[ (e_1+e_2)^{a}(e_1 e_2)^{b} e_1 e_3^{n-3}\cdots e_{n-1}=e_3^{n-3}\cdots e_{n-1}\sum_{i=0}^{a}\binom{a}{i}e_1^{i+1+b}e_2^{a-i+b}. \]

Note that by proposition 2.2(3) the only non-zero monomials in this sum are the ones for $i$ that satisfies $(i+1+b,\,a-i+b)\in \{(n-1,\,n-2),\,(n-2,\,n-1)\}$ and $\binom {a}{i}$ is odd, i.e. $i\in \{n-2-b,\,n-3-b\}$ and $\binom {a}{i}$ is odd.

If $i=n-2-b$, then $\binom {a}{i}=\binom {2(n-2-b)}{n-2-b}=\binom {2m}{m}$ (here $2m=2(n-2-b)=a$). By lemma 3.2 this number is odd only if $m=0$, i.e. $(a,\,b)=(0,\,n-2)$.

Let us now consider the case $i=n-3-b$. Then $\binom {a}{i}=\binom {2(n-2-b)}{n-3-b}=\binom {2m}{m-1}=\binom {2m}{m+1}$ (again $2m=2(n-2-b)=a$). By lemma 3.2 this number is odd if and only if $m=2^{l}-1$ for some $l\geqslant 1$. Then $a=2^{l+1}-2$ and $b=n-2^{l}-1\geqslant 0$, which completes our proof.

Remark 3.6 If $w_1^{a}w_2^{b}\neq 0$ and $a+2b=2(n-2),$ then, by proposition 2.1, $w_1^{a}w_2^{b}=w_2^{n-2}$ (since $w_2^{n-2}$ is the only non-zero class in $H^{2(n-2)}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$).

3.2 Some exact values

In this section we calculate $\mathrm {zcl}(G_2(\mathbb {R}^{n}))$ for $n=2^{s}+1$.

In the proof of the main result we will use the following observation. Let $n\geqslant 4$. Then, by proposition 2.1, every class in $H^{1}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$ is of the form $\alpha w_1$, $\alpha \in \mathbb {Z}_2$, while every class in $H^{2}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$ is of the form $\beta w_1^{2}+\gamma w_2$, $\beta,\,\gamma \in \mathbb {Z}_2$. Since $z(w_1^{2})=z(w_1)^{2}$, we conclude: if $\mathrm {zcl}(G_2(\mathbb {R}^{n}))=t$, then there are $a,\,b,\,c\in \mathbb {N}_0$ such that $z(w_1)^{a}z(w_2)^{b}z(x_1)\cdots z(x_c)\neq 0$, where $a+b+c=t$ and $x_1,\,\ldots,\,x_c$ are some classes of $H^{*}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$ each in dimension at least 3.

Proposition 3.7 For $s\geqslant 2$ and $n=2^{s}+1$ one has

\[ \mathrm{zcl}(G_2(\mathbb{R}^{n}))=2^{s+1}+2^{s}-4\quad\mbox{and}\quad\mathrm{TC}(G_2(\mathbb{R}^{n}))\geqslant 2^{s+1}+2^{s}-3. \]

Proof. First, we prove that $z(w_1)^{2^{s+1}-1}z(w_2)^{2^{s}-3}\neq 0$. After expanding, we consider all summands of the form $w_2^{n-2}\otimes x$, for some $x\in H^{*}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$. By lemma 3.5 each such summand is of the form $w_1^{2^{l+1}-2}w_2^{2^{s}-2^{l}}\otimes w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{l}-3}$ (for $l\geqslant 2$) with coefficient $\binom {2^{s+1}-1}{2^{l+1}-2}\binom {2^{s}-3}{2^{s}-2^{l}}$. By Lucas’ theorem each of these binomial coefficients is odd, so $z(w_1)^{2^{s+1}-1}z(w_2)^{2^{s}-3}$ contains $w_2^{n-2}\otimes \sum _{l=2}^{s}w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{l}-3}$. Since $w_2^{n-2}$ is the only non-zero class in $H^{2(n-2)}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$ (by proposition 2.1), it is enough to prove $\sum _{l=2}^{s}w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{l}-3}\neq 0$ (in $H^{*}(G_2(\mathbb {R}^{2^{s}+1});\mathbb {Z}_2)$).

Note that by lemma 2.4, $w_1^{2^{s}}w_2=0$, and so $w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{l}-3}=0$ for $2\leqslant l\leqslant s-1$. Hence, it is enough to prove that $w_1w_2^{2^{s}-3}=w_1w_2^{n-4}\neq 0$, which follows from the fact that $w_1w_2^{n-4}$ is in the additive basis $B_{2,n-2}$ (proposition 2.1). So, $\mathrm {zcl}(G_2(\mathbb {R}^{2^{s}+1}))\geqslant 2^{s+1}+2^{s}-4$.

Let us now prove that $\mathrm {zcl}(G_2(\mathbb {R}^{2^{s}+1}))\leqslant 2^{s+1}+2^{s}-4$. Suppose that this is not the case and let $a,\,b,\,c\in \mathbb {N}_0$ and $x_1,\,\ldots,\,x_c\in H^{*}(G_2(\mathbb {R}^{2^{s}+1});\mathbb {Z}_2)$ be some classes each in dimension at least 3, such that $a+b+c\geqslant 2^{s+1}+2^{s}-3$ and $z(w_1)^{a}z(w_2)^{b}z(x_1)\cdots z(x_c)\neq 0$. By lemma 2.3, we have $a+2b+3c\leqslant 4(2^{s}-1)-1=2^{s+2}-5$, and hence $b+2c\leqslant 2^{s}-2$. Furthermore, since $z(w_1)^{2^{s+1}}=0$ (by (2.3)), we have $a\leqslant 2^{s+1}-1$ and hence $b+c=(a+b+c)-a\geqslant 2^{s}-2$. This implies $b=2^{s}-2$ and $c=0$. Finally, $a+b+c\geqslant 2^{s+1}+2^{s}-3$ and $a\leqslant 2^{s+1}-1$ imply $a=2^{s+1}-1$.

So, it is enough to prove $A=z(w_1)^{2^{s+1}-1}z(w_2)^{2^{s}-2}=0$. Suppose that this is not the case. Note that the dimension of $A$ is $2^{s+1}-1+2(2^{s}-2)=4(n-2)-1$, so every summand of $A$ is of the form $x'\otimes x''$ where one of the classes $x'$ and $x''$ has dimension $2(n-2)$ and the other $2(n-2)-1$. Note that, by proposition 2.1, the only class in $H^{*}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$ of dimension $2(n-2)$ (resp. $2(n-2)-1$) is $w_2^{n-2}$ (resp. $w_1w_2^{n-3}$). By symmetry, this and $A\neq 0$ imply $A=w_2^{n-2}\otimes w_1w_2^{n-3}+w_1w_2^{n-3}\otimes w_2^{n-2}$. Now, we proceed as in the first part of the proof to prove that the coefficient of $w_2^{n-2}\otimes w_1w_2^{n-3}$ in $A$ is zero. By lemma 3.5 each such summand in $A=z(w_1)^{2^{s+1}-1}z(w_2)^{2^{s}-2}$ is of the form $w_1^{2^{l+1}-2}w_2^{2^{s}-2^{l}}\otimes w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{l}-2}$ (for some $1\leqslant l\leqslant s$) with coefficient $\binom {2^{s+1}-1}{2^{l+1}-2}\binom {2^{s}-2}{2^{s}-2^{l}}$. By Lucas’ theorem this coefficient is 1, so it is enough to prove $\sum _{l=1}^{s}w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{l}-2}=0$.

Again, by lemma 2.4, $w_1^{2^{s}}w_2=0$, so $w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{l}-2}=0$ for $2\leqslant l\leqslant s-1$. Hence, the previous sum is equal to $w_1^{2^{s+1}-3}+w_1w_2^{2^{s}-2}$. By (2.1), $w_1^{2^{s+1}-3}\neq 0$, so $w_1^{2^{s+1}-3}=w_1w_2^{n-3}=w_1w_2^{2^{s}-2}$, and hence $A=0$.

Remark 3.8 By proposition 3.1, $\mathrm {TC}(G_2(\mathbb {R}^{2^{s}+1}))\leqslant 2^{s+2}-4$, so there is a gap of $2^{s}-1$ between our lower bound and this bound. For example, $9\leqslant \mathrm {TC}(G_2(\mathbb {R}^{5})) \leqslant 12$.

Remark 3.9 Ideas from this paper can be used to prove the following:

1. (1) If $s\geqslant 1$, then $\mathrm {zcl}(G_2(\mathbb {R}^{2^{s}+2}))=3\cdot 2^{s}-2$ (one has $z(w_1)^{2^{s+1}-2}z(w_2)^{2^{s}}\neq 0$). So, by proposition 3.1, $3\cdot 2^{s}-1\leqslant \mathrm {TC}(G_2(\mathbb {R}^{2^{s}+2}))\leqslant 2^{s+2}-1$.

2. (2) If $s\geqslant 2$, then $\mathrm {zcl}(G_2(\mathbb {R}^{2^{s}+3}))=3\cdot 2^{s}$ (one has $z(w_1)^{2^{s+1}-1}z(w_2)^{2^{s}+1}\neq 0$). So, by proposition 3.1, $3\cdot 2^{s}+1\leqslant \mathrm {TC}(G_2(\mathbb {R}^{2^{s}+3}))\leqslant 2^{s+2}+3$.

Complete proofs of these results can be found in the extended version of this paper which is available on the author's website.

3.3 General bounds for $\mathrm {zcl}(G_2(\mathbb {R}^{n}))$

Let $2^{s}+4\leqslant n\leqslant 2^{s+1}$ and $t=n-2^{s}$. Also, we assume $s\geqslant 3$ (i.e. $n\neq 8$). Furthermore, let $r$ be the unique integer such that $2^{r-1}< t\leqslant 2^{r}$. Since $t\geqslant 4$, we have $r\geqslant 2$. Let $j$ be the smallest positive integer such that the digit on position $j$ in the binary representation of $t-2$ is equal to 1 ($j$ is well-defined since $t-2\geqslant 2$); in other words, $t-2$ has the binary representation of the following form

\[ t-2=2^{m}+\alpha_{m-1}2^{m-1}+\cdots+\alpha_{j+1}2^{j+1}+2^{j}+\alpha_0, \]

for some $\alpha _0,\,\alpha _{j+1},\,\alpha _{j+2},\,\ldots,\,\alpha _{m-1}\in \{0,\,1\}$ and $1\leqslant j\leqslant m$. Since $2^{m}\leqslant t-2\leqslant 2^{r}-2\leqslant 2^{s}-2$, we additionally have $1\leqslant j\leqslant m< r\leqslant s$.

Proposition 3.10 If $n,$ $s,$ $t,$ $r$ and $j$ are as above, then

\[ \mathrm{zcl}(G_2(\mathbb{R}^{n}))\geqslant 2^{s+1}+2^{s}+2^{r}-\varepsilon-2 \]

and $\mathrm {TC}(G_2(\mathbb {R}^{n}))\geqslant 2^{s+1}+2^{s}+2^{r}-\varepsilon -1$, where $\varepsilon =\left \{\begin {smallmatrix} 2^{j},\, & \mbox {if }t\mbox { is even} \\ 2^{j}+1,\, & \mbox {otherwise.} \end {smallmatrix}\right.$

Proof. It is enough to prove that $z(w_1)^{2^{s+1}-1}z(w_2)^{2^{s}+2^{r}-\varepsilon -1}\neq 0$. After expanding, we consider all summands of the form $w_2^{n-2}\otimes x$, for some $x\in H^{*}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$. By lemma 3.5 each such summand is of the form $w_1^{2^{l+1}-2}w_2^{2^{s}+t-2^{l}-1}\otimes w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{r}+2^{l}-\varepsilon -t}$, $0\leqslant l\leqslant s$, with coefficient $\alpha _l=\binom {2^{s+1}-1}{2^{l+1}-2}\binom {2^{s}+2^{r}-\varepsilon -1}{2^{s}+t-2^{l}-1}=\binom {2^{s}+2^{r}-\varepsilon -1}{2^{s}+t-2^{l}-1}$. (Note: if $2^{r}+2^{l}-\varepsilon -t<0$, then $2^{s}+2^{r}-\varepsilon -1<2^{s}+t-2^{l}-1$ and hence $\alpha _l=0$, so there is no need to discard summands $\alpha _lw_1^{2^{l+1}-2}w_2^{2^{s}+t-2^{l}-1}\otimes w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{r}+2^{l}-\varepsilon -t}$ when $2^{r}+2^{l}-\varepsilon -t<0$.) Since $w_2^{n-2}$ is the only non-zero class in $H^{2(n-2)}(G_2(\mathbb {R}^{n});\mathbb {Z}_2)$ (by proposition 2.1), it is enough to prove

\[ A=\sum_{l=0}^{s}\alpha_l w_1^{2^{s+1}-2^{l+1}+1}w_2^{2^{r}+2^{l}-\varepsilon-t}\neq 0\quad\mbox{in }H^{*}(G_2(\mathbb{R}^{n});\mathbb{Z}_2). \]

Let us first consider the case when $t$ is even. Then $\varepsilon =2^{j}$. Note that $2^{s}+2^{r}-2^{j}-1=2^{s}+2^{r-1}+2^{r-2}+\dots +2^{j+1}+2^{j-1}+2^{j-2}+\dots +1$ ($j< r$). So, by Lucas’ theorem, $\alpha _0$ and $\alpha _s$ are even (since both $2^{s}+t-2$ and $t-1$ have digit 1 on the $j$-th position in the binary representation), while $\alpha _j$ is odd (since $2^{s}+t-1-2^{j}$ has digit 0 on the $j$-th position in the binary representation).

Let us denote $\tau =2^{r}-2^{j}-t$. Note that $t-2+2^{j}\leqslant 2^{r}$, i.e. $\tau \geqslant -2$. By proposition 2.2.(4), $A\neq 0$ if and only if

\[ \sum_{l=0}^{s}\alpha_l (e_1+e_2)^{2^{s+1}-2^{l+1}+1}(e_1 e_2)^{2^{l}+\tau}\cdot e_1\cdot e_3^{n-3}e_4^{n-4}\cdots e_{n-1}\neq 0, \]

and, by part (b) of lemma 3.3, if and only if

\[ \displaystyle p_1=\sum_{l=0}^{s}\alpha_l (e_1+e_2)^{2^{s+1}-2^{l+1}+1}(e_1e_2)^{2^{l}+\tau}\cdot e_1\neq 0. \]

To prove that $p_1\neq 0$ we will use remark 3.4, i.e. we write $p_1$ as in remark 3.4 and find suitable indices $i'$ and $i''$ (as in that remark). We denote

\begin{align*} q_1& =\sum_{l=0}^{s}\alpha_l (e_1+e_2)^{2^{s+1}-2^{l+1}}(e_1e_2)^{2^{l}+\tau}=\sum_{l=0}^{s}\alpha_l (e_1^{2^{l+1}}+e_2^{2^{l+1}})^{2^{s-l}-1}(e_1e_2)^{2^{l}+\tau}\\ & =\sum_{l=0}^{s}\alpha_l\sum_{i=0}^{2^{s-l}-1}e_1^{i\cdot 2^{l+1}+2^{l}+\tau}e_2^{(2^{s-l}-1-i)\cdot 2^{l+1}+2^{l}+\tau}. \end{align*}

Let us observe a monomial $e_1^{a}e_2^{b}$ that appears in the inner sum for $l$. Then $a+b=2^{s+1}+2\tau$ and $a-b=(2i+1-2^{s-l})2^{l+1}$, i.e. $2^{l+1}\parallel a-b$ for $s\neq l$ (i.e. $2^{l+1}\mid a-b$ and $2^{l+2}\nmid a-b$) and $a=b$ for $s=l$; so, $e_1^{a}e_2^{b}$ appears only once in $q_1$ and its coefficient is $\alpha _l$. Now, since $\alpha _s$ is even this implies that the coefficient of $(e_1e_2)^{2^{s}+\tau }$ in $q_1$ is 0, and since $\alpha _0$ is even that the coefficients of $e_1^{2^{s}+\tau -1}e_2^{2^{s}+\tau +1}$ and $e_1^{2^{s}+\tau +2^{j}-1}e_2^{2^{s}+\tau -2^{j}+1}$ in $q_1$ are 0. On the other hand, since $\alpha _j$ is odd the coefficient of $e_1^{2^{s}+\tau +2^{j}}e_2^{2^{s}+\tau -2^{j}}$ in $q_1$ is 1.

Now, we expand $p_1=(e_1^{2}+e_1e_2)q_1$. Note that the degree of each monomial in $p_1$ is $2^{s+1}+2\tau +2=2^{s+1}+2^{r+1}-2t-2^{j+1}+2\leqslant 2^{s+1}+4(t-1)-2t-2=2n-6$, and hence, after removing all monomials of the form $e_1^{a}e_2^{b}$ when $a\geqslant n$ or $b\geqslant n$, we get $p_1$ written as in remark 3.4. Let us observe a monomial $e_1^{a}e_2^{b}$ in $p_1$. By the previous identity, its coefficient is the sum of coefficients of $e_1^{a-2}e_2^{b}$ and $e_1^{a-1}e_2^{b-1}$ in $q_1$. So, the coefficient of $(e_1e_2)^{2^{s}+\tau +1}$ is 0, while the coefficient of $e_1^{2^{s}+\tau +2^{j}+1}e_2^{2^{s}+\tau -2^{j}+1}$ is 1. Since $2^{s}+\tau +2^{j}+1=2^{s}+2^{r}-t+1\leqslant 2^{s}+t-1=n-1$, the degrees of $e_1$ and $e_2$ in these monomials are less than $n$, so we can apply lemma 3.3 and remark 3.4 to conclude $p_1\neq 0$.

Finally, we consider the case when $t$ is odd. Then $\varepsilon =2^{j}+1$. Note that $2^{s}+2^{r}-2^{j}-2=2^{s}+2^{r-1}+2^{r-2}+\dots +2^{j+1}+2^{j-1}+2^{j-2}+\dots +2$, while $t-2=2^{j+1}t'+2^{j}+1<2^{r}\leqslant 2^{s}$ for some $t'\geqslant 0$. So, by Lucas’ theorem, we have that $\alpha _0=\binom {2^{s}+2^{r}-2^{j}-2}{2^{s}+2^{j+1}t'+2^{j}+1}$ and $\alpha _1=\binom {2^{s}+2^{r}-2^{j}-2}{2^{s}+2^{j+1}t'+2^{j}}$ are even, while

\[ \alpha_2=\binom{2^{s}+2^{r}-2^{j}-2}{2^{s}+t-5}=\binom{2^{s}+2^{r-1}+\dots+2^{j+1}+2^{j-1}+\dots+2}{2^{s}+2^{j+1}t'+2^{j-1}+2^{j-2}+\dots+2} \]

is odd.

Let us denote $\theta =2^{r}-2^{j}-t-1$. Note that $2^{j}+t-2\leqslant 2^{r}+1$, i.e. $\theta \geqslant -4$. By proposition 2.2.(4), $A\neq 0$ if and only if

\[ \sum_{l=0}^{s}\alpha_l (e_1+e_2)^{2^{s+1}-2^{l+1}+1}(e_1 e_2)^{2^{l}+\theta}\cdot e_1\cdot e_3^{n-3}e_4^{n-4}\dots e_{n-1}\neq 0, \]

and, by lemma 3.3(b), if and only if $p_2=\sum _{l=0}^{s}\alpha _l (e_1+e_2)^{2^{s+1}-2^{l+1}+1}(e_1e_2)^{2^{l}+\theta } e_1$ is non-zero. Let us denote

\[ q_2=\sum_{l=0}^{s}\alpha_l (e_1+e_2)^{2^{s+1}-2^{l+1}}(e_1e_2)^{2^{l}+\theta}=\sum_{l=0}^{s}\alpha_l (e_1^{2^{l+1}}+e_2^{2^{l+1}})^{2^{s-l}-1}(e_1e_2)^{2^{l}+\theta}. \]

Now, as in the previous part of the proof we conclude: the coefficients of $e_1^{2^{s}+\theta -1}e_2^{2^{s}+\theta +1}$, $e_1^{2^{s}+\theta -2}e_2^{2^{s}+\theta +2}$ and $e_1^{2^{s}+\theta -3}e_2^{2^{s}+\theta +3}$ in $q_2$ are 0 (since $\alpha _0$ and $\alpha _1$ are even); the coefficient of $e_1^{2^{s}+\theta -4}e_2^{2^{s}+\theta +4}$ in $q_2$ is 1 (since $\alpha _2$ is odd). So, in the polynomial $p_2=(e_1^{2}+e_1e_2)q_2$ the coefficient of $e_1^{2^{s}+\theta }e_2^{2^{s}+\theta +2}$ is 0, while the coefficient of $e_1^{2^{s}+\theta -2}e_2^{2^{s}+\theta +4}$ is 1. Since the total degree of each monomial of $p_2$ is $2^{s+1}+2\theta +2=2^{s+1}+2^{r+1}-2^{j+1}-2t\leqslant 2^{s+1}+4t-8-2t=2n-8$ and $2^{s}+\theta +4=2^{s}+2^{r}-2^{j}-t+3\leqslant 2^{s}+2^{r}-t+1\leqslant 2^{s}+t-1=n-1$, we can apply lemma 3.3 and remark 3.4 to conclude $p_2\neq 0$.

4. Zero-divisor cup-length of $G_3(\mathbb {R}^{n})$

Let $s$ be the unique integer such that $2^{s}< n\leqslant 2^{s+1}$. In this section we give some bounds for $\mathrm {zcl}(G_3(\mathbb {R}^{n}))$.

In the following proposition we consider the case $n=2^{s}+1$. This result will show that the corresponding result of [9, theorem 4.8] is not correct (see also remark 4.2). Fortunately, this proposition gives a better lower bound for topological complexity.

Proposition 4.1 Let $n=2^{s}+1,$ where $s\geqslant 3$. Then

\[ \mathrm{zcl}(G_3(\mathbb{R}^{n}))\geqslant 2^{s+1}+2^{s}+2^{s-2}-7\mbox{ and }\mathrm{TC}(G_3(\mathbb{R}^{n}))\geqslant 2^{s+1}+2^{s}+2^{s-2}-6. \]

Proof. It is enough to show $A=z(w_1)^{2^{s+1}-1}z(w_2)^{2^{s-1}+2^{s-2}-2}z(w_3)^{2^{s-1}-4}\neq 0$.

First, we prove that $w_1^{2^{s}}w_3=0$. By proposition 2.2, this follows from

\begin{align*} p_3 & = \pi^{*}(w_1^{2^{s}}w_3)e_1^{2}e_2e_4^{n-4}\cdots e_{n-1}\\ & =(e_1+e_2+e_3)^{2^{s}}(e_1e_2e_3)e_1^{2}e_2e_4^{n-4}\cdots e_{n-1}\\ & =(e_1^{2^{s}+3}e_2^{2}e_3+e_1^{3}e_2^{2^{s}+2}e_3+e_1^{3}e_2^{2}e_3^{2^{s}+1})e_4^{n-4}\cdots e_{n-1}=0. \end{align*}

Since $w_1^{2^{s}}w_3=0$, we have

\begin{align*} A& =z(w_1)^{2^{s}-1}z(w_2)^{2^{s-1}+2^{s-2}-2}z(w_1^{2^{s}})z(w_3)^{2^{s-1}-4}\\ & =z(w_1)^{2^{s}-1}z(w_2)^{2^{s-1}+2^{s-2}-2}(w_1^{2^{s}}\otimes w_3^{2^{s-1}-4}+w_3^{2^{s-1}-4}\otimes w_1^{2^{s}}). \end{align*}

Let us observe all classes of the form $w_3^{n-3}\otimes x$ for some $x\in H^{*}(G_3(\mathbb {R}^{n});\mathbb {Z}_2)$ after expanding the expression for $A$; since $w_3^{n-3}$ is the only non-zero class in $H^{3(n-3)}(G_3(\mathbb {R}^{n});\mathbb {Z}_2)$ (by proposition 2.1), to prove that $A$ is non-zero it is enough to show that the sum of all such $x$ is non-zero. To do so, we determine all monomials $x'$ and $x''$ in classes $w_1$ and $w_2$, such that $w_1^{2^{s}}x'=w_3^{n-3}=w_3^{2^{s}-2}$ and $w_3^{2^{s-1}-4}x''=w_3^{2^{s}-2}$.

Let $x'=w_1^{a}w_2^{b}$ be such that $w_1^{2^{s}+a}w_2^{b}=w_3^{2^{s}-2}$. Then $a+2b=2(2^{s}-3)$. We use proposition 2.2:

\begin{align*} p_1 & = \pi^{*}(w_1^{2^{s}+a}w_2^{b})e_1^{2}e_2e_4^{n-4}\cdots e_{n-1}\\ & =(e_1^{2^{s}}+e_2^{2^{s}}+e_3^{2^{s}})(e_1+e_2+e_3)^{a}(e_1e_2+e_2e_3+e_3e_1)^{b}e_1^{2}e_2e_4^{n-4}\cdots e_{n-1}\\ & =e_3^{2^{s}}(e_1+e_2)^{a}(e_1e_2)^{b+1}e_1e_4^{n-4}\cdots e_{n-1}\\ & =e_3^{2^{s}}\sum_{i=0}^{a}\binom{a}{i}e_1^{i+b+2}e_2^{a-i+b+1}\cdot e_4^{n-4}\cdots e_{n-1}. \end{align*}

Note that by proposition 2.2(3) the only non-zero monomials in this sum are the ones for $i$ that satisfies $(i+b+2,\,a-i+b+1)\in \{(2^{s}-1,\,2^{s}-2),\,(2^{s}-2,\,2^{s}-1)\}$ and $\binom {a}{i}$ is odd, i.e. $i\in \{2^{s}-3-b,\,2^{s}-4-b\}$ and $\binom {a}{i}$ is odd.

If $i=2^{s}-3-b$, then $\binom {a}{i}=\binom {2(2^{s}-3-b)}{2^{s}-3-b}=\binom {2\delta }{\delta }$ (here $2\delta =2(2^{s}-3-b)=a$). By lemma 3.2, this number is odd only if $\delta =0$, i.e. $(a,\,b)=(0,\,2^{s}-3)$. Let us now consider the case $i=2^{s}-4-b$. Then $\binom {a}{i}=\binom {2(2^{s}-3-b)}{2^{s}-4-b}=\binom {2\delta }{\delta -1}=\binom {2\delta }{\delta +1}$. Again, by lemma 3.2, this number is odd only if $\delta =2^{l}-1$, and hence $a=2^{l+1}-2$ and $b=2^{s}-2^{l}-2$ for some $1\leqslant l\leqslant s-1$.

Let us now go back to our expression for $A$. Here we only consider pairs $(a,\,b)$ that satisfy $a\leqslant 2^{s}-1$ and $b\leqslant 2^{s-1}+2^{s-2}-2$; hence $b=2^{s}-2^{l}-2$ only if $l\in \{s-2,\,s-1\}$, so we have two pairs to consider: $(a,\,b)\in \{(2^{s-1}-2,\,2^{s-1}+2^{s-2}-2),\,(2^{s}-2,\,2^{s-1}-2)\}=P$.

Next, let $x''=w_1^{a'}w_2^{b'}$ be such that $w_1^{a'}w_2^{b'}w_3^{2^{s-1}-4}=w_3^{2^{s}-2}$. We denote the set of all such pairs $(a',\,b')$ with $P'$. Clearly, if $(a',\,b')\in P'$, then $a'+2b'=3(2^{s-1}+2)$, and hence $a'+b'\geqslant 3(2^{s-2}+1)$; also, by observing $A$, it is clear that $a'\leqslant 2^{s}-1$.

Now, to prove that $A$ is non-zero, it is enough to prove that $B$ is non-zero, where $B$ is equal to

\[ \sum_{(a,b)\in P}w_1^{2^{s}-1-a}w_2^{2^{s-1}+2^{s-2}-2-b}w_3^{2^{s-1}-4}+\sum_{(a',b')\in P'}w_1^{2^{s}+2^{s}-1-a'}w_2^{2^{s-1}+2^{s-2}-2-b'}. \]

By proposition 2.2.(4), this is equivalent to $p=\pi ^{*}(B)e_1^{2}e_2e_{4}^{n-4}\cdots e_{n-1}\neq 0$. In what follows we will be working with the additive basis

\[ \widetilde{B}_{2^{s}+1}=\{e_1^{a_1}e_2^{a_2}\cdots e_{2^{s}}^{a_{2^{s}}}\,|\,a_1\leqslant 2^{s}-1,\,a_2\leqslant 2^{s}-2,\,a_3\leqslant 2^{s},\,a_i\leqslant 2^{s}+1-i,\,i\geqslant 4\} \]

for $H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$, given by proposition 2.2(1) and the canonical homeomorphism $\sigma :\mathrm {Flag}(\mathbb {R}^{n})\rightarrow \mathrm {Flag}(\mathbb {R}^{n})$ defined by

\[ \sigma(L_1,L_2,L_3,L_4,L_5,\ldots,L_n)=(L_3,L_1,L_2,L_4,L_5,\ldots,L_n). \]

Let $d_{3,n-3}=e_1^{2}e_2e_4^{n-4}\cdots e_{n-1}$. Then

\begin{align*} p_2& =\pi^{*}\left(\sum_{(a,b)\in P}w_1^{2^{s}-1-a}w_2^{2^{s-1}+2^{s-2}-2-b}w_3^{2^{s-1}-4}\right)d_{3,n-3}\\ & =\pi^{*}(w_1^{2^{s-1}+1}w_3^{2^{s-1}-4}+w_1w_2^{2^{s-2}}w_3^{2^{s-1}-4})d_{3,n-3}\\ & =((e_1+e_2+e_3)^{2^{s-1}}+(e_1e_2+e_2e_3+e_3e_1)^{2^{s-2}})\\ & \phantom{=}\,\cdot(e_1+e_2+e_3)(e_1e_2e_3)^{2^{s-1}-4}d_{3,n-3}. \end{align*}

Note that the monomials of $p_2$ belong to $\widetilde {B}_{2^{s}+1}$; indeed, the degree of $e_1$ in each monomial is at most $2^{s-1}+1+2^{s-1}-4+2=2^{s}-1$, the degree of $e_2$ is at most $2^{s-1}+1+2^{s-1}-4+1=2^{s}-2$, and the degree of $e_3$ is at most $2^{s-1}+1+2^{s-1}-4=2^{s}-3$. In particular, each monomial of $p_2$ is not divisible by $e_3^{2^{s}}$. Finally, $p_2\neq 0$ since $e_1^{2^{s}-1}e_2^{2^{s-1}-3}e_3^{2^{s-1}-4}e_4^{n-4}\cdots e_{n-1}$ has coefficient 1 in $p_2$.

On the other hand,

\begin{align*} p_3& =\pi^{*}\left(\sum_{(a',b')\in P'}w_1^{2^{s}+2^{s}-1-a'}w_2^{2^{s-1}+2^{s-2}-2-b'}\right)d_{3,n-3}\\ & =\sum_{(a',b')\in P'}(e_1^{2^{s}}+e_2^{2^{s}}+e_3^{2^{s}})(e_1+e_2+e_3)^{2^{s}-1-a'}\\ & \quad\cdot(e_1e_2+e_2e_3+e_3e_1)^{2^{s-1}+2^{s-2}-2-b'}d_{3,n-3}\\ & =\sum_{(a',b')\in P'}e_3^{2^{s}}(e_1+e_2)^{2^{s}-1-a'}(e_1e_2)^{2^{s-1}+2^{s-2}-2-b'}d_{3,n-3}. \end{align*}

Since $a'+b'\geqslant 3(2^{s-2}+1)$, the degree of $e_1$ (resp. $e_2$) in each monomial of this sum is at most $2^{s}+2^{s-1}+2^{s-2}-1-a'-b'\leqslant 2^{s}-4$ (resp. $2^{s}+2^{s-1}+2^{s-2}-2-a'-b'\leqslant 2^{s}-5$), and hence, after expansion, each monomial (if any) of $p_3$ is in $\widetilde {B}_{2^{s}+1}$ and divisible by $e_3^{2^{s}}$ (note: it is possible that $p_3=0$).

Hence, $p_2$ and $p_3$ do not have any common monomials from $\widetilde {B}_{2^{s}+1}$, and so there are no cancellations between monomials of $p_2$ and $p_3$. Now, $p_2\neq 0$ implies $p=p_2+p_3\neq 0$.

Remark 4.2 Ideas from this paper can be used to prove the following: if $s\geqslant 4$, then $\mathrm {zcl}(G_3(\mathbb {R}^{2^{s}+2}))\geqslant 7\cdot 2^{s-1}$ (one has $z(w_1)^{2^{s+1}-1}z(w_2)^{2^{s}+2^{s-1}}z(w_3)\neq 0$). Hence, $\mathrm {TC}(G_3(\mathbb {R}^{2^{s}+2}))\geqslant 7\cdot 2^{s-1}+1$. Complete proof of this result can be found in the extended version of this paper which is available on the author's website.

Proposition 4.3 Let $s\geqslant 2,$ $n=2^{s}+t\leqslant 2^{s+1},$ $t\geqslant 3$ and $2^{r-1}< t\leqslant 2^{r}$. Then

\[ \mathrm{zcl}(G_3(\mathbb{R}^{n}))\geqslant 2^{s+2}-2^{r}-1\quad\mbox{and}\quad\mathrm{TC}(G_3(\mathbb{R}^{n}))\geqslant 2^{s+2}-2^{r}. \]

Also, if $t-3\geqslant 2^{s-1},$ then $\mathrm {zcl}(G_3(\mathbb {R}^{n}))\geqslant 7\cdot 2^{s-1}-1$ and $\mathrm {TC}(G_3(\mathbb {R}^{n}))\geqslant 7\cdot 2^{s-1}$.

Proof. For the first inequality it is enough to show

\[ A=z(w_1)^{2^{s+1}-1}z(w_2)^{2^{s+1}-2^{r+1}}z(w_3)^{2^{r}}\neq 0. \]

Note that $w_1^{2^{s}}w_3^{2^{r}}=0$. Indeed, this follows from proposition 2.2(4), $e_i^{2^{s}+2^{r}}=0$ for $i\in \{1,\,2,\,3\}$ and the following calculations:

\begin{align*} p_1 & = \pi^{*}(w_1^{2^{s}}w_3^{2^{r}})e_1^{2}e_2e_4^{n-4}\cdots e_{n-1}\\ & =(e_1^{2^{s}}+e_2^{2^{s}}+e_3^{2^{s}})(e_1e_2e_3)^{2^{r}}e_1^{2}e_2e_4^{n-4}\cdots e_{n-1}\\ & =(e_1^{2^{s}+2^{r}}e_2^{2^{r}}e_3^{2^{r}}+e_1^{2^{r}}e_2^{2^{s}+2^{r}}e_3^{2^{r}}+e_1^{2^{r}}e_2^{2^{r}}e_3^{2^{s}+2^{r}})e_1^{2}e_2e_4^{n-4}\cdots e_{n-1}=0. \end{align*}

Similarly, one proves that $w_2^{2^{s}}w_3^{2^{r}}=0$, $w_1^{2^{s}}w_2^{2^{s}+2^{r}}=0$ and $w_1^{2^{s}+2^{r}}w_2^{2^{s}}=0$.

Note that $2^{r}\geqslant t\geqslant 3$ implies $r\geqslant 2$. Now, we consider the cases $2\leqslant r\leqslant s-1$ and $r=s$ separately.

Case 1: $2\leqslant r\leqslant s-1$. We have

\begin{align*} A& =z(w_1)^{2^{s}-1}z(w_1)^{2^{s}}z(w_2)^{2^{s}-2^{r+1}}z(w_2)^{2^{s}}z(w_3)^{2^{r}}\\ & =z(w_1)^{2^{s}-1}z(w_2)^{2^{s}-2^{r+1}}(w_1^{2^{s}}w_2^{2^{s}}\otimes w_3^{2^{r}}+w_3^{2^{r}}\otimes w_1^{2^{s}}w_2^{2^{s}}). \end{align*}

Since $2^{s}-1=2^{s-1}+\dots +2^{r+1}+2^{r}+2^{r}-1$ and $2^{s}-2^{r+1}=2^{s-1}+\dots +2^{r+1}$, in a similar way we get

\[ A=z(w_1)^{2^{r}-1}(w_1^{2^{s}}w_2^{2^{s}}\otimes w_1^{2^{s}-2^{r}}w_2^{2^{s}-2^{r+1}}w_3^{2^{r}}+w_1^{2^{s}-2^{r}}w_2^{2^{s}-2^{r+1}}w_3^{2^{r}}\otimes w_1^{2^{s}}w_2^{2^{s}}). \]

Since the dimension of $w_1^{2^{s}}w_2^{2^{s}}$ is greater than the dimension of the class $w_1^{2^{s}-2^{r}}w_2^{2^{s}-2^{r+1}}w_3^{2^{r}}$, after expanding the expression for $A$, there is only one summand with the first coordinate in dimension $3\cdot 2^{s}+2^{r}-1$, and this summand is $w_1^{2^{s}+2^{r}-1}w_2^{2^{s}}\otimes w_1^{2^{s}-2^{r}}w_2^{2^{s}-2^{r+1}}w_3^{2^{r}}$. Hence, it is enough to prove that $w_1^{2^{s}+2^{r}-1}w_2^{2^{s}}\neq 0$ and $w_1^{2^{s}-2^{r}}w_2^{2^{s}-2^{r+1}}w_3^{2^{r}}\neq 0$.

First, we prove that $w_1^{2^{s}+2^{r}-1}w_2^{2^{s}}\neq 0$. Since $e_i^{2^{s+1}}=0$ for $i\in \{1,\,2,\,3\}$ (by proposition 2.2(2)), by proposition 2.2(4) it is enough to prove that

\begin{align*} p_2 & =\pi^{*}(w_1^{2^{s}+2^{r}-1}w_2^{2^{s}})e_1^{2}e_2e_4^{n-4}\cdots e_{n-1}\\ & =(e_1+e_2+e_3)^{2^{r}-1}(e_1^{2^{s}}+e_2^{2^{s}}+e_3^{2^{s}})(e_1e_2+e_2e_3+e_3e_1)^{2^{s}}e_1^{2}e_2e_4^{n-4}\cdots e_{n-1}\\ & =(e_1+e_2+e_3)^{2^{r}-1}(e_1e_2e_3)^{2^{s}}e_1^{2}e_2e_4^{n-4}\cdots e_{n-1}\\ & =\pi^{*}(w_1^{2^{r}-1}w_3^{2^{s}})e_1^{2}e_2e_4^{n-4}\cdots e_{n-1} \end{align*}

is non-zero in $H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$, i.e. that $w_1^{2^{r}-1}w_3^{2^{s}}$ is non-zero in $H^{*}(G_3(\mathbb {R}^{n});\mathbb {Z}_2)$. Observe the inclusion $i:G_3(\mathbb {R}^{n-2^{s}})\subset G_3(\mathbb {R}^{n})$. Note that the height of $i^{*}(w_1)$ in $H^{*}(G_3(\mathbb {R}^{n-2^{s}});\mathbb {Z}_2)$ is $2^{r}-1$ (by (2.1)). So, let $x$ be a class in $H^{*}(G_3(\mathbb {R}^{n-2^{s}});\mathbb {Z}_2)$ such that $i^{*}(w_1)^{2^{r}-1} x\in H^{3(n-2^{s}-3)}(G_3(\mathbb {R}^{n-2^{s}});\mathbb {Z}_2)$ is non-zero (this class exists by Poincare's duality); further, let $\widetilde {x}\in H^{*}(G_3(\mathbb {R}^{n});\mathbb {Z}_2)$ be such that $i^{*}(\widetilde {x})=x$. Then, by [12, lemma 1], the value of $w_1^{2^{r}-1}\widetilde {x}\cdot w_3^{2^{s}}$ is the same as the value of $i^{*}(w_1^{2^{r}-1} \widetilde {x})=i^{*}(w_1)^{2^{r}-1} x$, which is non-zero. Hence, $w_1^{2^{r}-1}w_3^{2^{s}}\neq 0$.

Finally, we prove that $w_1^{2^{s}-2^{r}}w_2^{2^{s}-2^{r+1}}w_3^{2^{r}}\neq 0$. This will immediately follow from the identity $w_1^{2^{s}-2^{r}}w_2^{2^{s}-2^{r}}w_3^{2^{r}}=w_1^{2^{s}}w_2^{2^{s}}=w_3^{2^{s}}\neq 0$, which we now prove. Since $e_i^{2^{s}+2^{r}}=0$ for $i\in \{1,\,2,\,3\}$, by proposition 2.2(4) this follows from (here $d_{3,n-3}=e_1^{2}e_2e_4^{n-4}\cdots e_{n-1}$)

\begin{align*} p_3 & =\pi^{*}(w_1^{2^{s}-2^{r}}w_2^{2^{s}-2^{r}}w_3^{2^{r}})d_{3,n-3}\\ & =(e_1+e_2+e_3)^{2^{s}-2^{r}}(e_1e_2+e_2e_3+e_3e_1)^{2^{s}-2^{r}}(e_1e_2e_3)^{2^{r}}d_{3,n-3}\\ & =(e_1+e_2+e_3)^{2^{s-1}}(e_1e_2+e_2e_3+e_3e_1)^{2^{s-1}}\\ & \quad\cdot(e_1+e_2+e_3)^{2^{s-1}-2^{r}}(e_1e_2+e_2e_3+e_3e_1)^{2^{s-1}-2^{r}}(e_1e_2e_3)^{2^{r}}d_{3,n-3}\\ & =(e_1+e_2+e_3)^{2^{s-1}-2^{r}}(e_1e_2+e_2e_3+e_3e_1)^{2^{s-1}-2^{r}}(e_1e_2e_3)^{2^{s-1}+2^{r}}d_{3,n-3}\\ & =\ \dots\\ & =(e_1e_2e_3)^{2^{s-1}+2^{s-2}+\cdots+2^{r}+2^{r}}d_{3,n-3}\\ & =(e_1e_2e_3)^{2^{s}}d_{3,n-3}\\ & =(e_1+e_2+e_3)^{2^{s}}(e_1e_2+e_2e_3+e_3e_1)^{2^{s}}d_{3,n-3}\\ & =\pi^{*}(w_1^{2^{s}}w_2^{2^{s}})d_{3,n-3}. \end{align*}

Since $w_3^{2^{s}}\in B_{3,n-3}$, we have $w_3^{2^{s}}\neq 0$, which completes our proof.

Case 2: $r=s$. Then $A=z(w_1)^{2^{s}-1}(w_1^{2^{s}}\otimes w_3^{2^{s}}+w_3^{2^{s}}\otimes w_1^{2^{s}})$. Since after expanding $A$ there is only one summand with the first coordinate in dimension $2^{s+2}-1$, and this summand is $w_1^{2^{s}-1}w_3^{2^{s}}\otimes w_1^{2^{s}}$, it is enough to prove $w_1^{2^{s}-1}w_3^{2^{s}}\neq 0$ and $w_1^{2^{s}}\neq 0$. The second follows from $w_1^{2^{s}}\in B_{3,n-3}$, and the first one is proven after the calculations for $p_2$.

Suppose now that $t-3\geqslant 2^{s-1}$. We will prove that

\[ B=z(w_1)^{2^{s+1}-1}z(w_2)^{2^{s}}z(w_3)^{2^{s-1}}\neq 0, \]

which implies $\mathrm {zcl}(G_3(\mathbb {R}^{n}))\geqslant 2^{s+1}+2^{s}+2^{s-1}-1$.

Let us observe all summands of $B$ with the first coordinate in dimension $9\cdot 2^{s-1}$. Note that

\[ B=z(w_1)^{2^{s}-1}z(w_1^{2^{s}})z(w_2^{2^{s}})z(w_3^{2^{s-1}}), \]

so the only monomial of this form is $w_1^{2^{s}}w_2^{2^{s}}w_3^{2^{s-1}}\otimes w_1^{2^{s}-1}$, and hence it is enough to prove that $w_1^{2^{s}}w_2^{2^{s}}w_3^{2^{s-1}}\neq 0$ and $w_1^{2^{s}-1}\neq 0$. This follows from lemma 2.4 (indeed, since $t-3\geqslant 2^{s-1}$, both monomials divide $w_1^{2^{s}}w_2^{2^{s}}w_3^{t-3}\neq 0$).

5. Zero-divisor cup-length of $G_k(\mathbb {R}^{n})$

In this section we give a lower bound for $G_k(\mathbb {R}^{n})$ for $k\geqslant 4$.

Proposition 5.1 Let $4\leqslant k< n$ and $2^{s}+k\leqslant n\leqslant 2^{s+1}$. Then

\[ \mathrm{zcl}(G_k(\mathbb{R}^{n}))\geqslant (\lceil \log_2 k\rceil+1)\cdot 2^{s}-1\quad\mbox{and}\quad \mathrm{TC}(G_k(\mathbb{R}^{n}))\geqslant (\lceil \log_2 k\rceil+1)\cdot 2^{s}. \]

Proof. Let $2^{r-1}< k\leqslant 2^{r}$. Then $\lceil \log _2 k\rceil =r$, so it is enough to prove

\[ A=z(w_1)^{2^{s+1}-1}\prod_{i=1}^{r-1}z(w_{2^{i}})^{2^{s}}=z(w_1)^{2^{s}-1}\prod_{i=0}^{r-1}z(w_{2^{i}}^{2^{s}})\neq 0. \]

First, let us prove that $p=\prod _{i=0}^{r-2}w_{2^{i}}^{2^{s}}$ is non-zero in $H^{*}(G_k(\mathbb {R}^{n});\mathbb {Z}_2)$. Let $d_{k,n-k}=e_1^{k-1}\cdots e_{k-1} e_{k+1}^{n-k-1}\cdots e_{n-1}$. Since $e_i^{2^{s+1}}=0$ for $1\leqslant i\leqslant k$ (by proposition 2.2(2)) and $k':=\sum _{i=0}^{r-2}2^{i}=2^{r-1}-1< k$ we have

\begin{align*} p_1 & =\pi^{*}\left(\prod_{i=0}^{r-2}w_{2^{i}}^{2^{s}}\right)d_{k,n-k} \\ & =\prod_{i=0}^{r-2}\left(\sum_{1\leqslant a_1< a_2<\cdots< a_{2^{i}}\leqslant k} e_{a_1}^{2^{s}}e_{a_2}^{2^{s}}\cdots e_{a_{2^{i}}}^{2^{s}}\right)d_{k,n-k} \\ & =[2^{0},2^{1},\ldots,2^{r-2}]\left(\sum_{1\leqslant a_1< a_2<\cdots < a_{{k'}}\leqslant k} e_{a_1}^{2^{s}}e_{a_2}^{2^{s}}\cdots e_{a_{k'}}^{2^{s}}\right) d_{k,n-k}, \end{align*}

where $[2^{0},\,2^{1},\,\ldots,\,2^{r-2}]=\binom {2^{0}+2^{1}+\dots +2^{r-2}}{2^{0}}\binom {2^{1}+\dots +2^{r-2}}{2^{1}}\cdots \binom {2^{r-2}}{2^{r-2}}$ denotes the multinomial coefficient. By Lucas’ theorem, this coefficient is odd. Also, for $1\leqslant i\leqslant k$ the degree of $e_i$ in each monomial in the last expression for $p_1$ is at most $2^{s}+k-i\leqslant n-i$, so all monomials in this expression are distinct members of the basis $B_n$ for $H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$, and hence $p_1\neq 0$. So, by proposition 2.2(4), $p\neq 0$.

Now, let us observe all summands after expanding $A$ with first coordinate in dimension $(2^{r-1}-1)\cdot 2^{s}$. The dimension of $p$ is $(2^{r-1}-1)\cdot 2^{s}$, and it is easy to see that the only term of this form is $p\otimes w_1^{2^{s}-1}w_{2^{r-1}}^{2^{s}}$. So, to finish the proof it is enough to prove $w_1^{2^{s}-1}w_{2^{r-1}}^{2^{s}}\neq 0$. In fact, we prove that $w_1^{2^{s}}w_{2^{r-1}}^{2^{s}}\neq 0$. Since $e_i^{2^{s+1}}=0$ for $1\leqslant i\leqslant k$, we have

\begin{align*} p_2 & = \pi^{*}\left(w_1^{2^{s}}w_{2^{r-1}}^{2^{s}}\right)d_{k,n-k} \\ & =\left(e_1^{2^{s}}+e_2^{2^{s}}+\cdots+e_k^{2^{s}}\right)\left(\sum_{1\leqslant a_1< a_2<\cdots< a_{2^{r-1}}\leqslant k} e_{a_1}^{2^{s}}e_{a_2}^{2^{s}}\cdots e_{a_{2^{r-1}}}^{2^{s}}\right)d_{k,n-k} \\ & =\left(\sum_{1\leqslant a_1< a_2<\cdots< a_{2^{r-1}+1}\leqslant k} e_{a_1}^{2^{s}}e_{a_2}^{2^{s}}\cdots e_{a_{2^{r-1}+1}}^{2^{s}}\right) d_{k,n-k}. \end{align*}

Now, as above, $2^{s}+k\leqslant n$ implies that all monomials in the last expression for $p_2$ are distinct members of the basis $B_n$ for $H^{*}(\mathrm {Flag}(\mathbb {R}^{n});\mathbb {Z}_2)$, and hence $p_2\neq 0$. By proposition 2.2(4), it follows that $w_1^{2^{s}}w_{2^{r-1}}^{2^{s}}\neq 0$.