Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Travis, C. C.
and
Yoshida, Norio
1981.
Oscillation criteria for third order hyperbolic characteristic initial value problems.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 88,
Issue. 1-2,
p.
135.
Hsiang, Wu-Teh
and
Kwong, Man Kam
1982.
Oscillation of second-order hyperbolic equations with non-integrable coefficients.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 91,
Issue. 3-4,
p.
305.
Travis, C.C.
and
Yoshida, Norio
1982.
Oscillation criteria for nonlinear Bianchi equations.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 6,
Issue. 6,
p.
625.
Kreith, Kurt
and
Pagan, Gordon
1983.
Qualitative theory for hyperbolic characteristic initial value problems.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 94,
Issue. 1-2,
p.
15.
Cheng, Sui Sun
1996.
Sturmian theorems for hyperbolic type partial difference equations.
Journal of Difference Equations and Applications,
Vol. 2,
Issue. 4,
p.
375.

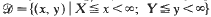 where (
where (