Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sinestrari, Carlo
1995.
Large time behaviour of solutions of balance laws with periodic initial data.
Nonlinear Differential Equations and Applications NoDEA,
Vol. 2,
Issue. 1,
p.
111.
Mascia, C.
1997.
Travelling wave solutions for a balance law.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 127,
Issue. 3,
p.
567.
Sinestrari, Carlo
1997.
Instability of Discontinuous Traveling Waves for Hyperbolic Balance Laws.
Journal of Differential Equations,
Vol. 134,
Issue. 2,
p.
269.
Sinestrari, Carlo
1997.
The Riemann Problem for an Inhomogeneous Conservation Law Without Convexity.
SIAM Journal on Mathematical Analysis,
Vol. 28,
Issue. 1,
p.
109.
Härterich, Jörg
1998.
Attractors of Viscous Balance Laws: Uniform Estimates for the Dimension.
Journal of Differential Equations,
Vol. 142,
Issue. 1,
p.
188.
Härterich, Jörg
1999.
Heteroclinic orbits between rotating waves in hyperbolic balance laws.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 129,
Issue. 3,
p.
519.
Fan, Haitao
Jin, Shi
and
Teng, Zhen-huan
2000.
Zero Reaction Limit for Hyperbolic Conservation Laws with Source Terms.
Journal of Differential Equations,
Vol. 168,
Issue. 2,
p.
270.
Dafermos, Constantine M.
2000.
Hyperbolic Conservation Laws in Continuum Physics.
Vol. 325,
Issue. ,
p.
209.
Cheverry, C
2000.
Regularizing effects for multidimensional scalar conservation laws.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 17,
Issue. 4,
p.
413.
Mascia, Corrado
2000.
Qualitative behavior of conservation laws with reaction term and nonconvex flux.
Quarterly of Applied Mathematics,
Vol. 58,
Issue. 4,
p.
739.
Hale, Jack K.
2001.
From Finite to Infinite Dimensional Dynamical Systems.
Vol. 19,
Issue. ,
p.
85.
Fan, Haitao
Jin, Shi
and
Miller, Judith R.
2003.
Wave patterns, stability, and slow motions in inviscid and viscous hyperbolic equations with stiff reaction terms.
Journal of Differential Equations,
Vol. 189,
Issue. 1,
p.
267.
Fan, Haitao
and
Jin, Shi
2003.
Front motion in multi-dimensional viscous conservation laws with stiff source terms driven by mean curvature and variation of front thickness.
Quarterly of Applied Mathematics,
Vol. 61,
Issue. 4,
p.
701.
2005.
Hyberbolic Conservation Laws in Continuum Physics.
Vol. 325,
Issue. ,
p.
511.
Fan, Haitao
and
Härterich, Jörg M.
2005.
Conservation laws with a degenerate source: Traveling waves, large-time behavior and zero relaxation limit.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 63,
Issue. 8,
p.
1042.
EHRT, JULIA
and
HÄRTERICH, JÖRG
2005.
ASYMPTOTIC BEHAVIOR OF SPATIALLY INHOMOGENEOUS BALANCE LAWS.
Journal of Hyperbolic Differential Equations,
Vol. 02,
Issue. 03,
p.
645.
Xu, Tianyuan
Jin, Chunhua
and
Ji, Shanming
2016.
Discontinuous traveling waves for scalar hyperbolic-parabolic balance law.
Boundary Value Problems,
Vol. 2016,
Issue. 1,
Duchêne, V.
and
Rodrigues, L. M.
2020.
Large-Time Asymptotic Stability of Riemann Shocks of Scalar Balance Laws.
SIAM Journal on Mathematical Analysis,
Vol. 52,
Issue. 1,
p.
792.
Duchêne, Vincent
and
Rodrigues, Luis Miguel
2022.
Stability and instability in scalar balance laws: fronts and periodic waves.
Analysis & PDE,
Vol. 15,
Issue. 7,
p.
1807.
Sahoo, Manas R.
Sen, Abhrojyoti
and
Singh, Manish
2024.
Initial boundary value problem for 1D scalar balance laws with strictly convex flux.
Journal of Mathematical Analysis and Applications,
Vol. 533,
Issue. 1,
p.
128006.
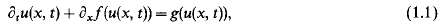
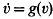 .
.
