Article contents
Positive solutions for a class of nonpositone problems with concave nonlinearities
Published online by Cambridge University Press: 14 November 2011
Abstract
We consider the bifurcation of positive solutions of the two-point boundary value problem
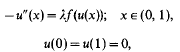
where λ> 0 is a real bifurcation parameter, and f ∊ C2 satisfies (fl) f(0) < 0, (f2) f′(s) > 0 for s > 0, (f3) f″(s) < 0 for s > 0 and (f4) limS→+∞f(s) = M where 0 < M ≦+∞. This problem has been studied by Casto and Shivaji under two additional hypotheses (f5) lims→+∞sf′(s) = 0, and (f6)f(θ)/θ < f′(θ), where θ is a positive number satisfying 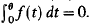 Assuming (fl)−(f6), Castro and Shivaji obtain some existence and nonexistence results and hence partial information on the bifurcation diagram, and they conjecture that this problem has at most two positive solutions. We prove this conjecture. Furthermore, we are able to generalise and improve their results under hypotheses (fl)−(f4). As a corollary, we show that there exists μ1 > 0 such that there exist no positive solutions for 0 <λ <μ1 and at most two positive solutions for μ1≦λ< + ∞, which improves a result of Brunovsky and Chow.
Assuming (fl)−(f6), Castro and Shivaji obtain some existence and nonexistence results and hence partial information on the bifurcation diagram, and they conjecture that this problem has at most two positive solutions. We prove this conjecture. Furthermore, we are able to generalise and improve their results under hypotheses (fl)−(f4). As a corollary, we show that there exists μ1 > 0 such that there exist no positive solutions for 0 <λ <μ1 and at most two positive solutions for μ1≦λ< + ∞, which improves a result of Brunovsky and Chow.
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 124 , Issue 3 , 1994 , pp. 507 - 515
- Copyright
- Copyright © Royal Society of Edinburgh 1994
References
- 4
- Cited by

