Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-11T12:10:57.306Z Has data issue: false hasContentIssue false
  • English
  • Français

Positivity and continued fractions from the binomial transformation

Part of: Elementary number theory Sequences and sets Combinatorics

Published online by Cambridge University Press:  18 March 2019

Bao-Xuan Zhu
Bao-Xuan Zhu*
Affiliation:
School of Mathematics and Statistics, Jiangsu Normal University, Xuzhou 221116, PR China (bxzhu@jsnu.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a sequence of polynomials 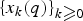$\{x_k(q)\}_{k \ges 0}$, define the transformation

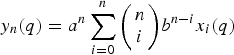$$y_n(q) = a^n\sum\limits_{i = 0}^n {\left( \matrix{n \cr i} \right)} b^{n-i}x_i(q)$$
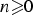for $n\ges 0$. In this paper, we obtain the relation between the Jacobi continued fraction of the ordinary generating function of yn(q) and that of xn(q). We also prove that the transformation preserves q-TPr+1 (q-TP) property of the Hankel matrix 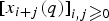$[x_{i+j}(q)]_{i,j \ges 0}$, in particular for r = 2,3, implying the r-q-log-convexity of the sequence 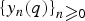$\{y_n(q)\}_{n\ges 0}$. As applications, we can give the continued fraction expressions of Eulerian polynomials of types A and B, derangement polynomials types A and B, general Eulerian polynomials, Dowling polynomials and Tanny-geometric polynomials. In addition, we also prove the strong q-log-convexity of derangement polynomials type B, Dowling polynomials and Tanny-geometric polynomials and 3-q-log-convexity of general Eulerian polynomials, Dowling polynomials and Tanny-geometric polynomials. We also present a new proof of the result of Pólya and Szegö about the binomial convolution preserving the Stieltjes moment property and a new proof of the result of Zhu and Sun on the binomial transformation preserving strong q-log-convexity.

Keywords

log-convexitystrong q-log-convexityk-q-log-convexitytotal positivityhankel matrixcontinued fraction

MSC classification

Primary: 05A10: Factorials, binomial coefficients, combinatorial functions
Secondary: 05A20: Combinatorial inequalities 05A30: $q$-calculus and related topics 11A55: Continued fractions 11B83: Special sequences and polynomials
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 149 , Issue 3 , June 2019 , pp. 831 - 847
Copyright
Copyright © Royal Society of Edinburgh 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Ahmia, M. and Belbachir, H.. Preserving log-convexity for generalized Pascal triangles. Electron. J. Combin. 19 (2012), Research Paper 16, 6 pp.Google Scholar
2Bagno, E. and Garber, D.. On the excedance number of colored permutation groups. Sém. Lothar. Combin. 53 (2004/2006), Article B53f, 17 pp.Google Scholar
3Barry, P.. Continued fractions and transformations of integer sequences. J. Integer Seq. 12 (2009), Article 09.7.6.Google Scholar
4Barry, P.. Eulerian polynomials as moments, via exponential Riordan arrays 14 (2011), Article 11.9.5, 14 pp.Google Scholar
5Barry, P.. General Eulerian polynomials as moments using exponential Riordan array. J. Integer Seq. 16 (2013), Article 13.9.6, 15 pp.Google Scholar
6Bennett, G.. Hausdorff means and moment sequences. Positivity 15 (2011), 17–48.Google Scholar
7Benoumhani, M.. On some numbers related to Whitney numbers of Dowling lattices. Adv. Appl. Math. 19 (1997), 106–116.Google Scholar
8Björner, A. and Brenti, F.. Combinatorics of Coxeter Groups. Grad. Texts in Math., vol. 231(New York: Springer-Verlag, 2005).Google Scholar
9Brenti, F.. Unimodal, log-concave, and Pólya frequency sequences in combinatorics. Thesis (Ph.D.)–Massachusetts Institute of Technology, 1988.Google Scholar
10Brenti, F.. Log-concave and unimodal sequences in algebra, combinatorics, and geometry: an update. Contemp. Math. 178 (1994), 71–89.Google Scholar
11Brenti, F.. Combinatorics and total positivity. J. Combin. Theory Ser. A 71 (1995), 175–218.Google Scholar
12Butler, L. M.. The q-log concavity of q-binomial coeffcients. J. Combin. Theory Ser. A 54 (1990), 54–63.Google Scholar
13Chen, W. Y. C.. Log-concavity and q-Log-convexity Conjectures on the Longest Increasing Subsequences of Permutations, arXiv: 0806.3392v2, 2008.Google Scholar
14Chen, W. Y. C., Tang, R. L. and Zhao, A. F. Y.. Derangement polynomials and excedances of type B. Electron. J. Combin. 16 (2009), R15.Google Scholar
15Chen, W. Y. C., Tang, R. L., Wang, L. X. W. and Yang, A. L. B.. The q-log-convexity of the Narayana polynomials of type B. Adv. in Appl. Math. 44 (2010), 85–110.Google Scholar
16Chen, W. Y. C., Wang, L. X. W. and Yang, A. L. B.. Schur positivity and the q-log-convexity of the Narayana polynomials. J. Algebraic Combin. 32 (2010), 303–338.Google Scholar
17Chen, W. Y. C., Wang, L. X. W. and Yang, A. L. B.. Recurrence relations for strongly q-log-convex polynomials. Canad. Math. Bull. 54 (2011), 217–229.Google Scholar
18Cheon, G.-S. and Jung, J.-H.. The r-Whitney numbers of Dowling lattices. Discrete Math. 312 (2012), 2337–2348.Google Scholar
19Comtet, L.. Advanced combinatorics. (Dordrecht: D. Reidel Publishing Co., 1974).Google Scholar
20Davenport, H. and Pólya, G.. On the product of two power series. Canadian J. Math. 1 (1949), 1–5.Google Scholar
21Dowling, T. A.. A class of geometric lattices based on finite groups. J. Combin. Theory Ser. B 14 (1973), 61–86; Erratum, J. Combin. Theory Ser. B 15 (1973), 211.Google Scholar
22Flajolet, P.. Combinatorial aspects of continued fractions. Discrete Math. 32 (1980), 125–161.Google Scholar
23Karlin, S.. Total Positivity, vol. I, (Stanford: Stanford University Press, 1968).Google Scholar
24Leroux, P.. Reduced matrices and q-log concavity properties of q-Stirling numbers. J. Combin. Theory Ser. A 54 (1990), 64–84.Google Scholar
25Liu, L. L. and Wang, Y.. On the log-convexity of combinatorial sequences. Adv. in. Appl. Math. 39 (2007), 453–476.Google Scholar
26Moll, V. H.. The evaluation of integrals: A personal story. Notices Amer. Math. Soc. 49 (2002), 311–317.Google Scholar
27Mongelli, P.. Excedances in classical and affine Weyl groups. Journal of Combinatorial Theory, Series A 120 (2013), 1216–1234.Google Scholar
28Pinkus, A.. Totally Positive Matrices. (Cambridge: Cambridge University Press, 2010).Google Scholar
29Pólya, G. and Szegö, G.. Problems and Theorems in Analysis, vol. II, 3rd ed. (New York: Springer-Verlag, 1964).Google Scholar
30Rahmani, M.. Some results on Whitney numbers of Dowling lattices. Arab J. Math. Sci. 20 (2014), 11–27.Google Scholar
31Sagan, B. E.. Log concave sequences of symmetric functions and analogs of the Jacobi-Trudi determinants. Trans. Amer. Math. Soc. 329 (1992), 795–811.Google Scholar
32Stanley, R. P.. Log-concave and unimodal sequences in algebra, combinatorics, and geometry. Ann. New York Acad. Sci. 576 (1989), 500–534.Google Scholar
33Su, X.-T., Wang, Y. and Yeh, Y.-N.. Unimodality Problems of Multinomial Coefficients and Symmetric Functions. Electron. J. Combin. 18 (2011), Research Paper 73.Google Scholar
34Tanny, S.. On some numbers related to the Bell numbers. Canad. Math. Bull. 17 (1975), 733–738.Google Scholar
35Wall, H. S.. Analytic Theory of Continued Fractions. (Princeton, NJ: Van Nostrand, 1948).Google Scholar
36Wang, Y. and Yeh, Y.-N.. Log-concavity and LC-positivity. J. Combin. Theory Ser. A 114 (2007), 195–210.Google Scholar
37Wang, Y. and Zhu, B.-X.. Log-convex and Stieltjes moment sequences. Adv. in Appl. Math. 81 (2016), 115–127.Google Scholar
38Xiong, T., Tsao, H.-P. and Hall, J. I.. General Eulerian numbers and the Eulerian polynomials. J. Math. (2013), Article 629132, 19 pp.Google Scholar
39Zhu, B.-X.. Log-convexity and strong q-log-convexity for some triangular arrays. Adv. in Appl. Math. 50 (2013), 595–606.Google Scholar
40Zhu, B.-X.. Some positivities in certain triangular arrays. Proc. Amer. Math. Soc. 142 (2014), 2943–2952.Google Scholar
41Zhu, B.-X.. Positivity of iterated sequences of polynomials. SIAM J. Discrete Math. 32 (2018), 1993–2010.Google Scholar
42Zhu, B.-X. and Sun, H.. Linear transformations preserving the strong q-log-convexity of polynomials. Electron. J. Combin. 22 (2015), P3.27.Google Scholar