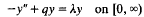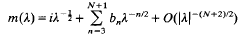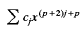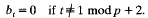Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Harris, B. J.
1987.
An exact method for the calculation of certain Titchmarsh-Weyl m-functions.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 106,
Issue. 1-2,
p.
137.
Harris, B.J.
1987.
The form of the spectral functions associated with a class of Sturm–Liouville equations with integrable coefficient.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 105,
Issue. 1,
p.
215.
Harris, B.J.
1988.
An inverse problem involving the Titchmarsh–Weyl m-function.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 110,
Issue. 3-4,
p.
305.
Atkinson, F. V.
and
Fulton, C. T.
1999.
Asymptotics of the Titchmarsh—Weyl m-coefficient for non-integrable potentials.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 129,
Issue. 4,
p.
663.