Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-14T04:50:53.291Z Has data issue: false hasContentIssue false
  • English
  • Français

Proximate topology and shape theory

Published online by Cambridge University Press:  14 November 2011

Zvonko Čerin
Zvonko Čerin
Affiliation:
Kopernikova 7, 41020 Zagreb, Croatia, e-mail: zcerin@x400.srce.hr
Get access Rights & Permissions [Opens in a new window]

Extract

Most of the development of shape theory was in the so-called outer shape theory, where the shape of spaces is described with the help of some outside objects.

This paper belongs to the so-called inner shape theory, in which the shape of spaces is described intrinsically without the use of any outside gadgets. We give a description of shape theory that does not need absolute neighbourhood retracts. We prove that the category ℋN whose objects are topological spaces and whose morphisms are proximate homotopy classes of proximate nets is naturally equivalent to the shape category 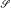h. The description of the category ℋN for compact metric spaces was given earlier by José M. R. Sanjurjo. We also give three applications of this new approach to shape theory.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 125 , Issue 3 , 1995 , pp. 595 - 615
Copyright
Copyright © Royal Society of Edinburgh 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Aló, R. A. and Shapiro, H. L.. Normal Topological Spaces (Cambridge: Cambridge University Press, 1972).Google Scholar
2Artin, M. and Mazur, B.. Etale Homotopy, Lecture Notes in Mathematics 100 (Berlin: Springer, 1969).CrossRefGoogle Scholar
3Bogatyi, S.. Approximate and fundamental retracts. Math. Sb. 22 (1974), 91–103.CrossRefGoogle Scholar
4Borsuk, K.. Concerning homotopy properties of compacta. Fund. Math. 62 (1968), 223–54.CrossRefGoogle Scholar
5Čerin, Z.. Homotopy properties of locally compact spaces at infinity—calmness and smoothness. Pacific J. Math. 79 (1978), 69–91.CrossRefGoogle Scholar
6Clapp, M. H.. On a generalization of absolute neighbourhood retracts. Fund. Math. 70 (1971), 117–30.CrossRefGoogle Scholar
7Dold, A.. Lectures on Algebraic Topology (Berlin: Springer, 1972).CrossRefGoogle Scholar
8Felt, J. E., ε-continuity and shape. Proc. Amer. Math. Soc. 46 (1974), 426–30.Google Scholar
9Ho, C.. On a stability theorem for the fixed point property. Fund. Math. 64 (1969), 181–8.Google Scholar
10Hu, S. T.. Theory of Retracts (Detroit: Wayne State University Press, 1965).Google Scholar
11Klee, V. L. and Yandl, A.. Some proximate concepts in topology. Symposia Mathematica, Publ. Inst. Naz. di Alta Matematica 16, pp. 21–39 (New York: Academic Press, 1974).Google Scholar
12Kozlowski, G.. Images of ANR's (preprint).Google Scholar
13Mardešić, S. and Segal, J.. Shape Theory (Amsterdam: North Holland, 1982).Google Scholar
14Morita, K.. On shapes of topological spaces. Fund. Math. 86 (1975), 251–9.CrossRefGoogle Scholar
15Sanjurjo, J.. A non-continuous description of the shape category of compacta. Quart. J. Math. Oxford (2) 40 (1989), 351–9.CrossRefGoogle Scholar