We study radial symmetry of entire solutions of the equation
0.1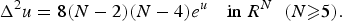 $$\Delta ^2u = 8(N-2)(N-4)e^u\quad {\rm in}\;R^N\;\;(N \ges 5).$$
$$\Delta ^2u = 8(N-2)(N-4)e^u\quad {\rm in}\;R^N\;\;(N \ges 5).$$
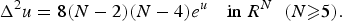 $$\Delta ^2u = 8(N-2)(N-4)e^u\quad {\rm in}\;R^N\;\;(N \ges 5).$$
$$\Delta ^2u = 8(N-2)(N-4)e^u\quad {\rm in}\;R^N\;\;(N \ges 5).$$