Article contents
Regularity results for equilibria in a variational model for fracture
Published online by Cambridge University Press: 14 November 2011
Synopsis
In recent years models describing interactions between fracture and damage have been proposed in which the relaxed energy of the material is given by a functional involving bulk and interfacial terms, of the form
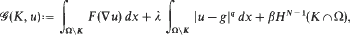
where Ω is an open, bounded subset of ℝN, q ≧1, g ∈ L∞ (Ω ℝN), λ, β > 0, the bulk energy density F is quasiconvex, K⊂ℝN is closed, and the admissible deformation u:Ω→ ℝN is C1 in Ω\K One of the main issues has to do with regularity properties of the ‘crack site’ K for a minimising pair (K, u). In the scalar case, i.e. when uΩ→ ℝ, similar models were adopted to image segmentation problems, and the regularity of the ‘edge’ set K has been successfully resolved for a quite broad class of convex functions F with growth p > 1 at infinity. In turn, this regularity entails the existence of classical solutions. The methods thus used cannot be carried out to the vectorial case, except for a very restrictive class of integrands. In this paper we deal with a vector-valued case on the plane, obtaining regularity for minimisers of 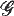 corresponding to polyconvex bulk energy densities of the form
corresponding to polyconvex bulk energy densities of the form
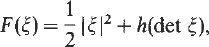
where the convex function h grows linearly at infinity.
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 127 , Issue 5 , 1997 , pp. 889 - 902
- Copyright
- Copyright © Royal Society of Edinburgh 1997
References
- 3
- Cited by

