Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Evans, W. D.
and
Ibrahim, Sobhy E.
1990.
Boundary conditions for general ordinary differential operators and their adjoints.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 114,
Issue. 1-2,
p.
99.
Benammar, M.
1992.
Classification of regularly solvable first-order differential operators.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 120,
Issue. 1-2,
p.
165.
Ibrahim, Sobhy E.
1992.
Nonself-adjoint Differential Operators in Direct Sum Spaces.
Rocky Mountain Journal of Mathematics,
Vol. 22,
Issue. 3,
Ibrahim, Sobhy El-sayed
1994.
Singular non-selfadjoint differential operators.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 124,
Issue. 4,
p.
825.
Ibrahim, Sobhy E.
1995.
Non Self-Adjoint Quasi-Differential Operators with Discrete Spectra.
Rocky Mountain Journal of Mathematics,
Vol. 25,
Issue. 3,
Ibrahim, Sobhy El-Sayed
1995.
The Point Spectra and Regularity Fields of Non-Self-Adjoint Quasi-Differential Operators.
Rocky Mountain Journal of Mathematics,
Vol. 25,
Issue. 2,
Ibrahim, Sobhy El-sayed
1995.
The spectra of well-posed operators.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 125,
Issue. 6,
p.
1331.
Frentzen, Hilbert
1998.
Boundary conditions for quasi-differential operators in L p spaces.
Results in Mathematics,
Vol. 33,
Issue. 3-4,
p.
274.
Ibrahim, Sobhy El-Sayed
1999.
On the Essential Spectra of Regularly Solvable Operators in the Direct Sum Spaces.
Rocky Mountain Journal of Mathematics,
Vol. 29,
Issue. 2,
Sobhy El-sayed, I.
Faried, N.
and
Attia, G. M.
2001.
On the L2w-Solutions of General Second-Order Nonsymmetric Differential Equations.
Siberian Mathematical Journal,
Vol. 42,
Issue. 1,
p.
174.
Ibrahim, Sobhy El-Sayed
2004.
The Spectra of General Differential Operators in the Direct Sum Spaces.
Czechoslovak Mathematical Journal,
Vol. 54,
Issue. 1,
p.
9.
Ibrahim, Sobhy El-Sayed
2013.
The Products of Regularly Solvable Operators with Their Spectra in Direct Sum Spaces.
Advances in Pure Mathematics,
Vol. 03,
Issue. 04,
p.
415.
Yang, Wei-hua
2015.
Symplectic structures of two kinds of nonsymmetric differential operators.
Acta Mathematicae Applicatae Sinica, English Series,
Vol. 31,
Issue. 2,
p.
543.

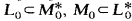 . In this paper, we study closed operators
. In this paper, we study closed operators 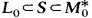 and are regularly solvable in the sense of Višik. The abstract results obtained are applied to operators generated by second-order linear differential expressions in a weighted space
and are regularly solvable in the sense of Višik. The abstract results obtained are applied to operators generated by second-order linear differential expressions in a weighted space 