Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-06T04:11:10.587Z Has data issue: false hasContentIssue false
  • English
  • Français

Right-angled Artin groups, polyhedral products and the 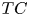${{\sf {TC}}}$-generating function

Part of: Classical Topics in Algebraic Topology

Published online by Cambridge University Press:  11 June 2021

Jorge Aguilar-Guzmán ,
Jesús González Open the ORCID record for Jesús González [Opens in a new window]  and
John Oprea
Jorge Aguilar-Guzmán
Affiliation:
Departamento de Matemáticas, Centro de Investigación y de Estudios Avanzados del I.P.N., México City 07000, Mexico (jaguzman@math.cinvestav.mx; jesus@math.cinvestav.mx)
Jesús González
Affiliation:
Departamento de Matemáticas, Centro de Investigación y de Estudios Avanzados del I.P.N., México City 07000, Mexico (jaguzman@math.cinvestav.mx; jesus@math.cinvestav.mx)
John Oprea
Affiliation:
Department of Mathematics, Cleveland State University, Cleveland, Ohio 44115, USA (jfoprea@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

For a graph 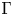$\Gamma$, let 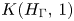$K(H_{\Gamma },\,1)$ denote the Eilenberg–Mac Lane space associated with the right-angled Artin (RAA) group 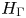$H_{\Gamma }$ defined by 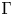$\Gamma$. We use the relationship between the combinatorics of $\Gamma$ and the topological complexity of 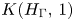$K(H_{\Gamma },\,1)$ to explain, and generalize to the higher TC realm, Dranishnikov's observation that the topological complexity of a covering space can be larger than that of the base space. In the process, for any positive integer 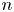$n$, we construct a graph 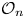$\mathcal {O}_n$ whose TC-generating function has polynomial numerator of degree 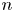$n$. Additionally, motivated by the fact that 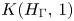$K(H_{\Gamma },\,1)$ can be realized as a polyhedral product, we study the LS category and topological complexity of more general polyhedral product spaces. In particular, we use the concept of a strong axial map in order to give an estimate, sharp in a number of cases, of the topological complexity of a polyhedral product whose factors are real projective spaces. Our estimate exhibits a mixed cat-TC phenomenon not present in the case of RAA groups.

Keywords

Axial mapgenerating functionLusternik–Schnirelmann categorypolyhedral productright-angled Artin grouptopological complexity

MSC classification

Primary: 55M30: Ljusternik-Schnirelman (Lyusternik-Shnirel'man) category of a space
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 3 , June 2022 , pp. 649 - 673
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adem, J., Gitler, S. and James, I. M.. On axial maps of a certain type. Bol. Soc. Mat. Mexicana 17 (1972), 59–62.Google Scholar
Bahri, A., Bendersky, M., Cohen, F. R. and Gitler, S.. The polyhedral product functor: a method of decomposition for moment-angle complexes, arrangements and related spaces. Adv. Math. 225 (2010), 1634–1668.CrossRefGoogle Scholar
Basabe, I., González, J., Rudyak, Y. B. and Tamaki, D.. Higher topological complexity and its symmetrization. Algebr. Geom. Topol. 14 (2014), 2103–2124.CrossRefGoogle Scholar
Cadavid-Aguilar, N., González, J., Gutiérrez, D., Guzmán-Sáenz, A. and Lara, A.. Sequential motion planning algorithms in real projective spaces: an approach to their immersion dimension. Forum Math. 30 (2018), 397–417.CrossRefGoogle Scholar
Cohen, D. C. and Farber, M.. Topological complexity of collision-free motion planning on surfaces. Compos. Math. 147 (2011), 649–660.CrossRefGoogle Scholar
Cornea, O., Lupton, G., Oprea, J. and Tanré, D.. Lusternik–Schnirelmann Category, Surveys and Monographs 103 (Providence: Amer. Math. Soc., 2003).CrossRefGoogle Scholar
Dranishnikov, A.. Topological complexity of wedges and covering maps. Proc. Am. Math. Soc. 142 (2014), 4365–4376.CrossRefGoogle Scholar
Dranishnikov, A. and Sadykov, R.. The topological complexity of the free product. Math. Z. 293 (2019), 407–416.CrossRefGoogle Scholar
Eilenberg, S. and Ganea, T.. On the Lusternik–Schnirelmann category of abstract groups. Ann. Math. 65 (1957), 517–518.CrossRefGoogle Scholar
Farber, M.. Topological complexity of motion planning. Discrete Comput. Geom. 29 (2003), 211–221.CrossRefGoogle Scholar
Farber, M.. Invitation to topological robotics, Zurich Lectures in Advanced Mathematics (Zürich: European Mathematical Society, 2008).CrossRefGoogle Scholar
Farber, M., Grant, M., Lupton, G. and Oprea, J.. Bredon cohomology and robot motion planning. Algebr. Geom. Topol. 19 (2019), 2023–2059.CrossRefGoogle Scholar
Farber, M., Grant, M., Lupton, G. and Oprea, J.. An upper bound for topological complexity. Topol. Appl. 255 (2019), 109–125.CrossRefGoogle Scholar
Farber, M., Kishimoto, D. and Stanley, D.. Generating functions and topological complexity. Topol. Appl. 278 (2020), 107235, 5 pp.CrossRefGoogle Scholar
Farber, M. and Mescher, S.. On the topological complexity of aspherical spaces. J. Topol. Anal. 12 (2020), 293–319.CrossRefGoogle Scholar
Farber, M. and Oprea, J.. Higher topological complexity of aspherical spaces. Topol. Appl. 258 (2019), 142–160.CrossRefGoogle Scholar
Farber, M., Tabachnikov, S. and Yuzvinsky, S.. Motion planning in projective spaces. Int. Math. Res. Not. 34 (2003), 1853–1870.CrossRefGoogle Scholar
Félix, Y. and Tanré, D.. Rational homotopy of the polyhedral product functor. Proc. Am. Math. Soc. 137 (2009), 891–898.CrossRefGoogle Scholar
García-Calcines, J. M.. A note on covers defining relative and sectional categories. Topol. Appl. 265 (2019), 106810.CrossRefGoogle Scholar
González, J., Gutiérrez, B. and Yuzvinsky, S.. Higher topological complexity of subcomplexes of products of spheres and related polyhedral product spaces. Topol. Methods Nonlinear Anal. 48 (2016), 419–451.Google Scholar
Grant, M., Lupton, G. and Oprea, J.. A mapping theorem for topological complexity. Algebr. Geom. Topol. 15 (2015), 1643–1666.10.2140/agt.2015.15.1643CrossRefGoogle Scholar
Grant, M., Lupton, G. and Oprea, J.. New lower bounds for the topological complexity of aspherical spaces. Topol. Appl. 189 (2015), 78–91.10.1016/j.topol.2015.04.005CrossRefGoogle Scholar
Kim, S. and Koberda, T.. Embeddability between right-angled Artin groups. Geom. Topol. 17 (2013), 493–530.CrossRefGoogle Scholar
Oprea, J. and Strom, J.. Mixing categories. Proc. Am. Math. Soc. 139 (2011), 3383–3392.CrossRefGoogle Scholar
Ostrand, P.. Dimension of metric spaces and Hilbert's problem $13$. Bull. Am. Math. Soc. 71 (1965), 619–622.10.1090/S0002-9904-1965-11363-5CrossRefGoogle Scholar
Rudyak, Y.. On higher analogues of topological complexity. Topol. Appl. 157 (2010), 916–920. Erratum in Topol. Appl. 157, (2010), 1118.10.1016/j.topol.2009.12.007CrossRefGoogle Scholar
Rudyak, Y.. On topological complexity of Eilenberg–MacLane spaces. Topol. Appl. 48 (2016), 65–67.Google Scholar
Sanderson, B. J.. A non-immersion theorem for real projective spaces. Topology 2 (1963), 209–211.CrossRefGoogle Scholar
Schwarz, A.. The genus of a fiber space. Am. Math. Soc. Transl. 55 (1966), 49–140.Google Scholar
Stanley, D.. On the Lusternik–Schnirelmann category of maps. Can. J. Math. 54 (2002), 608–633.10.4153/CJM-2002-022-6CrossRefGoogle Scholar