Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T12:38:27.301Z Has data issue: false hasContentIssue false
  • English
  • Français

A rigorous proof of an exponentially small estimate for a boundary value arising from an ordinary differential equation

Published online by Cambridge University Press:  14 November 2011

J. G. B. Byatt-Smith  and
A. M. Davie
J. G. B. Byatt-Smith
Affiliation:
Department of Mathematics, University of Edinburgh, James Clerk Maxwell Building, The King's Buildings, Mayfield Road, Edinburgh EH9 3JZ, U.K.
A. M. Davie
Affiliation:
Department of Mathematics, University of Edinburgh, James Clerk Maxwell Building, The King's Buildings, Mayfield Road, Edinburgh EH9 3JZ, U.K.
Get access Rights & Permissions [Opens in a new window]

Synopsis

The equation

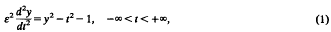
has a solution y(t) which is non-oscillating on the interval (0, ∞) and has the asymptotic expansion

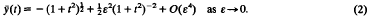
Each term of this expansion is even in t so that formally 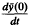is zero to all orders of ɛ. The estimate of 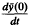has been obtained by Byatt-Smith [3] who corrects (2) in the complex plane near t = i where the series ceases to be valid. This requires asolution of the equation

the equation for the first Painlevé transcedent. Here we prove rigorously that this method gives the correct asymptotic estimate

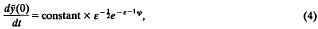
where

The proof involves converting (1) and (3) to integral equations. The existence and uniqueness of these integral equations are established by use of the contraction mapping theorem. We also prove that the appropriate solution to (3) provides a uniformly valid approximation to (2) over a suitably defined region of the complex plane.

We also consider the connection problem for the oscillatory solutions of (1) which have asymptotic expansions

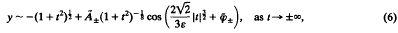
where Ã+, Ã− φ+, and φ− are constants. The connection problem is to determine the asymptotic expansion at +∞ of a solution which has a given asymptotic expansion at −∞. In other words, we wish to find (Ã+,φ+) as a function of Ã−and φ−. We prove that there is a unique solution to the connection problem, provided Ã− is small enough, and obtain bounds on the estimate of Ã+

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 114 , Issue 3-4 , 1990 , pp. 243 - 258
Copyright
Copyright © Royal Society of Edinburgh 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Arnold, V. I., Geometric Methods in the Theory of Ordinary DifferentialEquations, 2nd edn. (Berlin: Springer, 1988).Google Scholar
2Byatt-Smith, J. G. B.. Resonant oscillations in shallow water with small mean square disturbances. J. Fluid Mech. 193 (1988), 369–390.CrossRefGoogle Scholar
3Byatt-Smith, J. G. B.. On the solutions of a second order differential equation arising in the theory of resonant oscillations in a tank. Stud. Appl. Math. 80 (1989), 109–135.CrossRefGoogle Scholar
4Chapman, P. B. and Mahony, J. J.. Reflection of waves in a slowly varying medium. SIAM J. Appl. Math. 34 (1978), 303–319.CrossRefGoogle Scholar
5Hastings, S. P. and Troy, W. C.. On some conjectures of Turcotte, Bau and Holmes. SIAM. J. Math. Anal. 20 (1989), 634–642.CrossRefGoogle Scholar
6Hille, E.. Lectures on Ordinary Differential Equations (New York: Addison-Wesley, 1969).Google Scholar
7Ince, E. L.. Ordinary Differential Equations (New York: Dover, 1956).Google Scholar
8Neistadt, A. I.. Differential'nye Uravneniya 23 (1987), 2060–2067; English translation: J. Differential Equations 23 (1987), 1385–1391.Google Scholar
9Neistadt, A. I.. Differential'nye Uravneniya 24 (1988), 226–233; English translation: J. Differential Equations 24 (1987), 171–176.Google Scholar
10Ockendon, H., Ockendon, J. R. and Johnson, A. D.. Resonant sloshing in shallow water. J. Fluid Mech. 167 (1986), 465–479.CrossRefGoogle Scholar