No CrossRef data available.
Published online by Cambridge University Press: 24 July 2023
Suppose $2< p<\infty$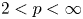 and $\varphi$
and $\varphi$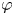 is a holomorphic self-map of the open unit disk $\mathbb {D}$
is a holomorphic self-map of the open unit disk $\mathbb {D}$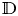 . We show the following assertions:
. We show the following assertions:
(1) If $\varphi$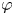 has bounded valence and0.1\begin{equation} \int_{\mathbb{D}} \left(\frac{1-|z|^2}{1-|\varphi(z)|^2}\right)^{p/2}\frac{\mathrm{d} A(z)}{(1-|z|^2)^2}<\infty, \end{equation}then $C_{\varphi }$
has bounded valence and0.1\begin{equation} \int_{\mathbb{D}} \left(\frac{1-|z|^2}{1-|\varphi(z)|^2}\right)^{p/2}\frac{\mathrm{d} A(z)}{(1-|z|^2)^2}<\infty, \end{equation}then $C_{\varphi }$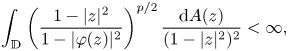
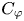 is in the Schatten $p$
is in the Schatten $p$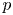 -class of the Hardy space $H^2$
-class of the Hardy space $H^2$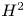 .
.
(2) There exists a holomorphic self-map $\varphi$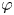 (which is, of course, not of bounded valence) such that the inequality (0.1) holds and $C_{\varphi }: H^2\to H^2$
(which is, of course, not of bounded valence) such that the inequality (0.1) holds and $C_{\varphi }: H^2\to H^2$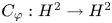 does not belong to the Schatten $p$
does not belong to the Schatten $p$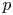 -class.
-class.