Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Corduneanu, C.
and
Lakshmikantham, V.
1980.
Equations with unbounded delay: a survey.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 4,
Issue. 5,
p.
831.
Webb, G. F.
1981.
Nonlinear semigroups and age-dependent population models.
Annali di Matematica Pura ed Applicata,
Vol. 129,
Issue. 1,
p.
43.
Villella-Bressan, Rosanna
1981.
Nonlinear Differential Equations.
p.
347.
Kartsatos, A. G.
and
Parrott, M. E.
1984.
A method of lines for a nonlinear abstract functional evolution equation.
Transactions of the American Mathematical Society,
Vol. 286,
Issue. 1,
p.
73.
Kartsatos, A. G.
and
Parrott, M. E.
1984.
Infinite-Dimensional Systems.
Vol. 1076,
Issue. ,
p.
115.
Fitzgibbon, W. E.
1987.
Dynamics of Infinite Dimensional Systems.
p.
105.
Grabosch, Annette
1989.
Translation semigroups and their linearizations on spaces of integrable functions.
Transactions of the American Mathematical Society,
Vol. 311,
Issue. 1,
p.
357.
Ruess, Wolfgang M.
1993.
The evolution operator approach to functional-differential equations with delay.
Proceedings of the American Mathematical Society,
Vol. 119,
Issue. 3,
p.
783.
Ruess, W. M.
and
Summers, W. H.
1994.
Operator semigroups for functional-differential equations with delay.
Transactions of the American Mathematical Society,
Vol. 341,
Issue. 2,
p.
695.
Lan, Nguyen Thanh
1999.
On Nonautonomous Functional Differential Equations.
Journal of Mathematical Analysis and Applications,
Vol. 239,
Issue. 1,
p.
158.
Lin, Chin-Yuan
2001.
The method of lines for solving a class of abstract differential equations.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 45,
Issue. 4,
p.
383.
Ha, Ki Sik
2003.
Nonlinear Functional Evolutions in Banach Spaces.
p.
31.
Lin, Chin-Yuan
2003.
Functional evolution equations.
Journal of Mathematical Analysis and Applications,
Vol. 285,
Issue. 2,
p.
463.
Ghavidel, Seyedeh Marzieh
2008.
Flow invariance for solutions to nonlinear nonautonomous partial differential delay equations.
Journal of Mathematical Analysis and Applications,
Vol. 345,
Issue. 2,
p.
854.
Ruess, Wolfgang
2009.
Flow invariance for nonlinear partial differential delay equations.
Transactions of the American Mathematical Society,
Vol. 361,
Issue. 8,
p.
4367.
Ruess, Wolfgang M.
2011.
Parabolic Problems.
Vol. 80,
Issue. ,
p.
591.
Ruess, Wolfgang M.
and
Ghavidel, Seyedeh Marzieh
2012.
Flow invariance for nonautonomous nonlinear partial differential delay equations.
Communications on Pure and Applied Analysis,
Vol. 11,
Issue. 6,
p.
2351.
Dong, Qixiang
and
Li, Gang
2014.
EXISTENCE OF SOLUTIONS FOR NONLINEAR EVOLUTION EQUATIONS WITH INFINITE DELAY.
Bulletin of the Korean Mathematical Society,
Vol. 51,
Issue. 1,
p.
43.
Tanaka, Naoki
2021.
Well‐posedness for fully nonlinear functional differential equations.
Mathematische Nachrichten,
Vol. 294,
Issue. 8,
p.
1595.


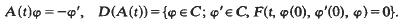
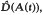 which is determined.
which is determined.