Hostname: page-component-6bb9c88b65-6scc2 Total loading time: 0 Render date: 2025-07-23T22:25:16.684Z Has data issue: false hasContentIssue false
  • English
  • Français

Symmetry breaking and multiple solutions for a Neumann problem in an exterior domain

Published online by Cambridge University Press:  14 November 2011

Vittorio Coti Zelati  and
Maria J. Esteban
Vittorio Coti Zelati
Affiliation:
SISSA, Strada Costiera, 11, 34014 Trieste, Italy
Maria J. Esteban
Affiliation:
Université Pierre et Marie Curie, Laboratoire d'Analyse Numérique, 75252 Paris Cedex 05, France
Get access Rights & Permissions [Opens in a new window]

Synopsis

In this paper we prove existence of multiple positive solutions for a Neumann problem in ℝN/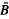(0, R), R large, with a superquadratic and odd nonlinearity. The proof is based on the fact that in such a situation the minimum of the corresponding energy functional (which is achieved) is not an even function and that there is quite a large gap (for large R) between such a minimum and the minimum of the same functional on even functions. In the set of functions whose energy lies in such a gap, we can apply index theory to prove the desired multiplicity result.

Information

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 116 , Issue 3-4 , 1990 , pp. 327 - 339
Copyright
Copyright © Royal Society of Edinburgh 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

1Benci, V.. On critical point theory for indefinite functionals in the presence of symmetries. Trans. Amer. Math. Soc. 274 (1982), 533–572.CrossRefGoogle Scholar
2Berestycki, H. and Lions, P. L.. Nonlinear scalar field equations. Arch. Rational Mech. Mat. 82 (1983), 313–346.CrossRefGoogle Scholar
3Browder, F.. Nonlinear eigenvalues problems and group invariance. Functional Analysis and Related Fields, (Proceedings of a Conference held in Chicago, 1968), 1–58 (Berlin: Springer, 1970).Google Scholar
4Esteban, M. J.. Rupture de symétrie pour des problèmes de Neumann sur-linéaires dans des ouverts extérieurs. C. R. Acad. Sci. Paris Sér. I. Math. 308 (1989), 281–286.Google Scholar
5Esteban, M. J.. Nonsymmetric ground states of a symmetric variational problem (to appear).Google Scholar
6Gidas, B., Ni, W. M. and Nirenberg, L.. Symmetry of positive solutions of nonlinear elliptic equations in ℝN. Adv. Math. Suppl. Studies 7 (1981), 369–402.Google Scholar
7Krasnoselskii, M. A.. Topological Methods in the Theory of Nonlinear Integral Equations (New York: Macmillan 1964).Google Scholar
8Lions, P. L.. The concentration-compactness principle in the calculus of variations. The locally compact case. Parts I and II. Ann. Inst. H. Poincaré, Anal. Non Linéaire 1 (1984), 109–145; 223–283.CrossRefGoogle Scholar
9Lions, P. L.. On positive solutions of semilinear elliptic equations in unbounded domains. In Nonlinear Diffusion Equations and their Equilibrium States, eds Ni, W. M., Peletier, L., Serrin, J. (Berlin: Springer 1988).Google Scholar
10Rabinowitz, P. H.. Variational methods for nonlinear eigenvalues problems. In Eigenvalues of Non-Linear Problems (III ciclo C.I.M.E., Varenna 1974), 139–195 (Rome: Edizioni Cremonese 1974).Google Scholar
11Rabinowitz, P. H.. Minimax methods in critical point theory with applications to differential equations. CBMS Regional Conference Series in Mathematics (1986)CrossRefGoogle Scholar