No CrossRef data available.
Article contents
A system of order 2 in which small sub-harmonics and large sub-harmonics coexist
Published online by Cambridge University Press: 14 November 2011
Synopsis
This paper establishes the coexistence of small and large subharmonics in a special case of the ordinary non-linear differential equation

of order 2, where κ, ε are small parameters, λ>0 is a parameter independent of κ, ε, h(t) has the least period 2π and
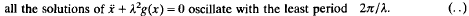
It is divided into three sections. In Section 1 a general analysis of the periodic solutions of (.), classified into small, medium or large, is given. In Section 2 the general theory of Section 1 is applied to the special form of (.) where k = vε1+s, v>0, s>0 constants, to obtain results from which we extract in Section 2 a theorem (Section 3) on the coexistence of a small periodic solution of order 1, several small sub-harmonics and several large sub-harmonics of the special case
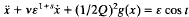
of (.), where Q≧1 is an integer.
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 108 , Issue 1-2 , 1988 , pp. 35 - 44
- Copyright
- Copyright © Royal Society of Edinburgh 1988

